Probably Approximately Precision and Recall Learning

Precision and Recall are foundational metrics in machine learning where both accurate predictions and comprehensive coverage are essential, such as in recommender systems and multi-label learning. In these tasks, balancing precision (the proportion of relevant items among those predicted) and recall (the proportion of relevant items successfully predicted) is crucial. A key challenge is that one-sided feedback--where only positive examples are observed during training--is inherent in many practical problems. For instance, in recommender systems like YouTube, training data only consists of videos that a user has actively selected, while unselected items remain unseen. Despite this lack of negative feedback in training, avoiding undesirable recommendations at test time is essential. We introduce a PAC learning framework where each hypothesis is represented by a graph, with edges indicating positive interactions, such as between users and items. This framework subsumes the classical binary and multi-class PAC learning models as well as multi-label learning with partial feedback, where only a single random correct label per example is observed, rather than all correct labels. Our work uncovers a rich statistical and algorithmic landscape, with nuanced boundaries on what can and cannot be learned. Notably, classical methods like Empirical Risk Minimization fail in this setting, even for simple hypothesis classes with only two hypotheses. To address these challenges, we develop novel algorithms that learn exclusively from positive data, effectively minimizing both precision and recall losses. Specifically, in the realizable setting, we design algorithms that achieve optimal sample complexity guarantees. In the agnostic case, we show that it is impossible to achieve additive error guarantees--as is standard in PAC learning--and instead obtain meaningful multiplicative approximations.

Utilizing Adversarial Examples for Bias Mitigation and Accuracy Enhancement

We propose a novel approach to mitigate biases in computer vision models by utilizing counterfactual generation and fine-tuning. While counterfactuals have been used to analyze and address biases in DNN models, the counterfactuals themselves are often generated from biased generative models, which can introduce additional biases or spurious correlations. To address this issue, we propose using adversarial images, that is images that deceive a deep neural network but not humans, as counterfactuals for fair model training. Our approach leverages a curriculum learning framework combined with a fine-grained adversarial loss to fine-tune the model using adversarial examples. By incorporating adversarial images into the training data, we aim to prevent biases from propagating through the pipeline. We validate our approach through both qualitative and quantitative assessments, demonstrating improved bias mitigation and accuracy compared to existing methods. Qualitatively, our results indicate that post-training, the decisions made by the model are less dependent on the sensitive attribute and our model better disentangles the relationship between sensitive attributes and classification variables.

Learnability Gaps of Strategic Classification

In contrast with standard classification tasks, strategic classification involves agents strategically modifying their features in an effort to receive favorable predictions. For instance, given a classifier determining loan approval based on credit scores, applicants may open or close their credit cards to fool the classifier. The learning goal is to find a classifier robust against strategic manipulations. Various settings, based on what and when information is known, have been explored in strategic classification. In this work, we focus on addressing a fundamental question: the learnability gaps between strategic classification and standard learning. We essentially show that any learnable class is also strategically learnable: we first consider a fully informative setting, where the manipulation structure (which is modeled by a manipulation graph $G^\star$) is known and during training time the learner has access to both the pre-manipulation data and post-manipulation data. We provide nearly tight sample complexity and regret bounds, offering significant improvements over prior results. Then, we relax the fully informative setting by introducing two natural types of uncertainty. First, following Ahmadi et al. (2023), we consider the setting in which the learner only has access to the post-manipulation data. We improve the results of Ahmadi et al. (2023) and close the gap between mistake upper bound and lower bound raised by them. Our second relaxation of the fully informative setting introduces uncertainty to the manipulation structure. That is, we assume that the manipulation graph is unknown but belongs to a known class of graphs. We provide nearly tight bounds on the learning complexity in various unknown manipulation graph settings. Notably, our algorithm in this setting is of independent interest and can be applied to other problems such as multi-label learning.

Bayesian Strategic Classification

In strategic classification, agents modify their features, at a cost, to ideally obtain a positive classification from the learner's classifier. The typical response of the learner is to carefully modify their classifier to be robust to such strategic behavior. When reasoning about agent manipulations, most papers that study strategic classification rely on the following strong assumption: agents fully know the exact parameters of the deployed classifier by the learner. This often is an unrealistic assumption when using complex or proprietary machine learning techniques in real-world prediction tasks. We initiate the study of partial information release by the learner in strategic classification. We move away from the traditional assumption that agents have full knowledge of the classifier. Instead, we consider agents that have a common distributional prior on which classifier the learner is using. The learner in our model can reveal truthful, yet not necessarily complete, information about the deployed classifier to the agents. The learner's goal is to release just enough information about the classifier to maximize accuracy. We show how such partial information release can, counter-intuitively, benefit the learner's accuracy, despite increasing agents' abilities to manipulate. We show that while it is intractable to compute the best response of an agent in the general case, there exist oracle-efficient algorithms that can solve the best response of the agents when the learner's hypothesis class is the class of linear classifiers, or when the agents' cost function satisfies a natural notion of submodularity as we define. We then turn our attention to the learner's optimization problem and provide both positive and negative results on the algorithmic problem of how much information the learner should release about the classifier to maximize their expected accuracy.

Incentivized Collaboration in Active Learning

In collaborative active learning, where multiple agents try to learn labels from a common hypothesis, we introduce an innovative framework for incentivized collaboration. Here, rational agents aim to obtain labels for their data sets while keeping label complexity at a minimum. We focus on designing (strict) individually rational (IR) collaboration protocols, ensuring that agents cannot reduce their expected label complexity by acting individually. We first show that given any optimal active learning algorithm, the collaboration protocol that runs the algorithm as is over the entire data is already IR. However, computing the optimal algorithm is NP-hard. We therefore provide collaboration protocols that achieve (strict) IR and are comparable with the best known tractable approximation algorithm in terms of label complexity.

Sequential Strategic Screening

We initiate the study of strategic behavior in screening processes with multiple classifiers. We focus on two contrasting settings: a conjunctive setting in which an individual must satisfy all classifiers simultaneously, and a sequential setting in which an individual to succeed must satisfy classifiers one at a time. In other words, we introduce the combination of strategic classification with screening processes. We show that sequential screening pipelines exhibit new and surprising behavior where individuals can exploit the sequential ordering of the tests to zig-zag between classifiers without having to simultaneously satisfy all of them. We demonstrate an individual can obtain a positive outcome using a limited manipulation budget even when far from the intersection of the positive regions of every classifier. Finally, we consider a learner whose goal is to design a sequential screening process that is robust to such manipulations, and provide a construction for the learner that optimizes a natural objective.

Eliciting User Preferences for Personalized Multi-Objective Decision Making through Comparative Feedback

In classic reinforcement learning (RL) and decision making problems, policies are evaluated with respect to a scalar reward function, and all optimal policies are the same with regards to their expected return. However, many real-world problems involve balancing multiple, sometimes conflicting, objectives whose relative priority will vary according to the preferences of each user. Consequently, a policy that is optimal for one user might be sub-optimal for another. In this work, we propose a multi-objective decision making framework that accommodates different user preferences over objectives, where preferences are learned via policy comparisons. Our model consists of a Markov decision process with a vector-valued reward function, with each user having an unknown preference vector that expresses the relative importance of each objective. The goal is to efficiently compute a near-optimal policy for a given user. We consider two user feedback models. We first address the case where a user is provided with two policies and returns their preferred policy as feedback. We then move to a different user feedback model, where a user is instead provided with two small weighted sets of representative trajectories and selects the preferred one. In both cases, we suggest an algorithm that finds a nearly optimal policy for the user using a small number of comparison queries.

Modeling Attrition in Recommender Systems with Departing Bandits

Traditionally, when recommender systems are formalized as multi-armed bandits, the policy of the recommender system influences the rewards accrued, but not the length of interaction. However, in real-world systems, dissatisfied users may depart (and never come back). In this work, we propose a novel multi-armed bandit setup that captures such policy-dependent horizons. Our setup consists of a finite set of user types, and multiple arms with Bernoulli payoffs. Each (user type, arm) tuple corresponds to an (unknown) reward probability. Each user's type is initially unknown and can only be inferred through their response to recommendations. Moreover, if a user is dissatisfied with their recommendation, they might depart the system. We first address the case where all users share the same type, demonstrating that a recent UCB-based algorithm is optimal. We then move forward to the more challenging case, where users are divided among two types. While naive approaches cannot handle this setting, we provide an efficient learning algorithm that achieves $\tilde{O}(\sqrt{T})$ regret, where $T$ is the number of users.

Finding Safe Zones of policies Markov Decision Processes

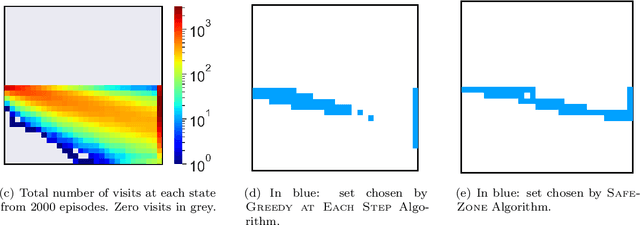
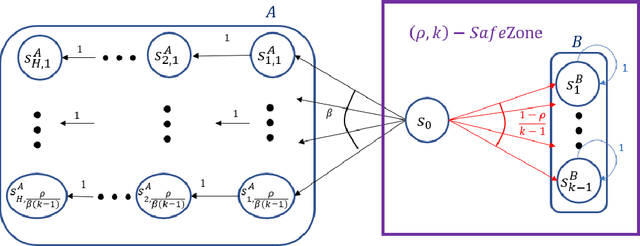
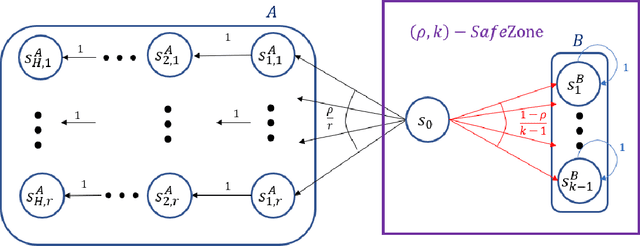
Given a policy, we define a SafeZone as a subset of states, such that most of the policy's trajectories are confined to this subset. The quality of the SafeZone is parameterized by the number of states and the escape probability, i.e., the probability that a random trajectory will leave the subset. SafeZones are especially interesting when they have a small number of states and low escape probability. We study the complexity of finding optimal SafeZones, and show that in general the problem is computationally hard. For this reason we concentrate on computing approximate SafeZones. Our main result is a bi-criteria approximation algorithm which gives a factor of almost $2$ approximation for both the escape probability and SafeZone size, using a polynomial size sample complexity. We conclude the paper with an empirical evaluation of our algorithm.

Dueling Bandits with Team Comparisons

We introduce the dueling teams problem, a new online-learning setting in which the learner observes noisy comparisons of disjoint pairs of $k$-sized teams from a universe of $n$ players. The goal of the learner is to minimize the number of duels required to identify, with high probability, a Condorcet winning team, i.e., a team which wins against any other disjoint team (with probability at least $1/2$). Noisy comparisons are linked to a total order on the teams. We formalize our model by building upon the dueling bandits setting (Yue et al.2012) and provide several algorithms, both for stochastic and deterministic settings. For the stochastic setting, we provide a reduction to the classical dueling bandits setting, yielding an algorithm that identifies a Condorcet winning team within $\mathcal{O}((n + k \log (k)) \frac{\max(\log\log n, \log k)}{\Delta^2})$ duels, where $\Delta$ is a gap parameter. For deterministic feedback, we additionally present a gap-independent algorithm that identifies a Condorcet winning team within $\mathcal{O}(nk\log(k)+k^5)$ duels.