Test-time regression: a unifying framework for designing sequence models with associative memory

Sequences provide a remarkably general way to represent and process information. This powerful abstraction has placed sequence modeling at the center of modern deep learning applications, inspiring numerous architectures from transformers to recurrent networks. While this fragmented development has yielded powerful models, it has left us without a unified framework to understand their fundamental similarities and explain their effectiveness. We present a unifying framework motivated by an empirical observation: effective sequence models must be able to perform associative recall. Our key insight is that memorizing input tokens through an associative memory is equivalent to performing regression at test-time. This regression-memory correspondence provides a framework for deriving sequence models that can perform associative recall, offering a systematic lens to understand seemingly ad-hoc architectural choices. We show numerous recent architectures -- including linear attention models, their gated variants, state-space models, online learners, and softmax attention -- emerge naturally as specific approaches to test-time regression. Each architecture corresponds to three design choices: the relative importance of each association, the regressor function class, and the optimization algorithm. This connection leads to new understanding: we provide theoretical justification for QKNorm in softmax attention, and we motivate higher-order generalizations of softmax attention. Beyond unification, our work unlocks decades of rich statistical tools that can guide future development of more powerful yet principled sequence models.

Interpretable Mechanistic Representations for Meal-level Glycemic Control in the Wild

Diabetes encompasses a complex landscape of glycemic control that varies widely among individuals. However, current methods do not faithfully capture this variability at the meal level. On the one hand, expert-crafted features lack the flexibility of data-driven methods; on the other hand, learned representations tend to be uninterpretable which hampers clinical adoption. In this paper, we propose a hybrid variational autoencoder to learn interpretable representations of CGM and meal data. Our method grounds the latent space to the inputs of a mechanistic differential equation, producing embeddings that reflect physiological quantities, such as insulin sensitivity, glucose effectiveness, and basal glucose levels. Moreover, we introduce a novel method to infer the glucose appearance rate, making the mechanistic model robust to unreliable meal logs. On a dataset of CGM and self-reported meals from individuals with type-2 diabetes and pre-diabetes, our unsupervised representation discovers a separation between individuals proportional to their disease severity. Our embeddings produce clusters that are up to 4x better than naive, expert, black-box, and pure mechanistic features. Our method provides a nuanced, yet interpretable, embedding space to compare glycemic control within and across individuals, directly learnable from in-the-wild data.

Sequence Modeling with Multiresolution Convolutional Memory

Efficiently capturing the long-range patterns in sequential data sources salient to a given task -- such as classification and generative modeling -- poses a fundamental challenge. Popular approaches in the space tradeoff between the memory burden of brute-force enumeration and comparison, as in transformers, the computational burden of complicated sequential dependencies, as in recurrent neural networks, or the parameter burden of convolutional networks with many or large filters. We instead take inspiration from wavelet-based multiresolution analysis to define a new building block for sequence modeling, which we call a MultiresLayer. The key component of our model is the multiresolution convolution, capturing multiscale trends in the input sequence. Our MultiresConv can be implemented with shared filters across a dilated causal convolution tree. Thus it garners the computational advantages of convolutional networks and the principled theoretical motivation of wavelet decompositions. Our MultiresLayer is straightforward to implement, requires significantly fewer parameters, and maintains at most a $\mathcal{O}(N\log N)$ memory footprint for a length $N$ sequence. Yet, by stacking such layers, our model yields state-of-the-art performance on a number of sequence classification and autoregressive density estimation tasks using CIFAR-10, ListOps, and PTB-XL datasets.

Learning Absorption Rates in Glucose-Insulin Dynamics from Meal Covariates

Traditional models of glucose-insulin dynamics rely on heuristic parameterizations chosen to fit observations within a laboratory setting. However, these models cannot describe glucose dynamics in daily life. One source of failure is in their descriptions of glucose absorption rates after meal events. A meal's macronutritional content has nuanced effects on the absorption profile, which is difficult to model mechanistically. In this paper, we propose to learn the effects of macronutrition content from glucose-insulin data and meal covariates. Given macronutrition information and meal times, we use a neural network to predict an individual's glucose absorption rate. We use this neural rate function as the control function in a differential equation of glucose dynamics, enabling end-to-end training. On simulated data, our approach is able to closely approximate true absorption rates, resulting in better forecast than heuristic parameterizations, despite only observing glucose, insulin, and macronutritional information. Our work readily generalizes to meal events with higher-dimensional covariates, such as images, setting the stage for glucose dynamics models that are personalized to each individual's daily life.

Is Importance Weighting Incompatible with Interpolating Classifiers?

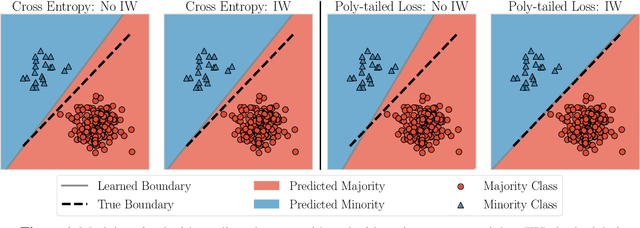
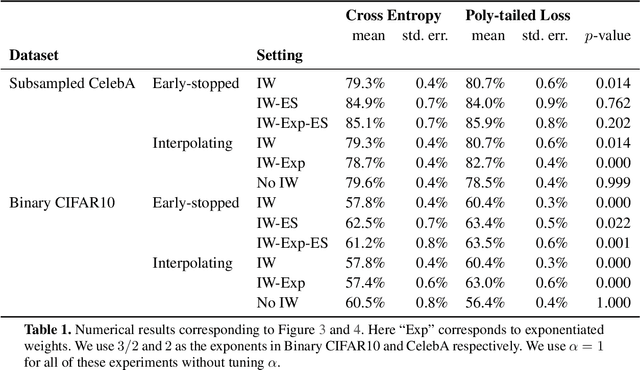
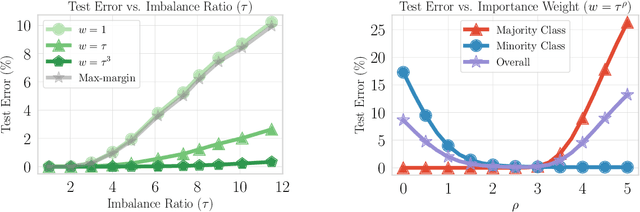
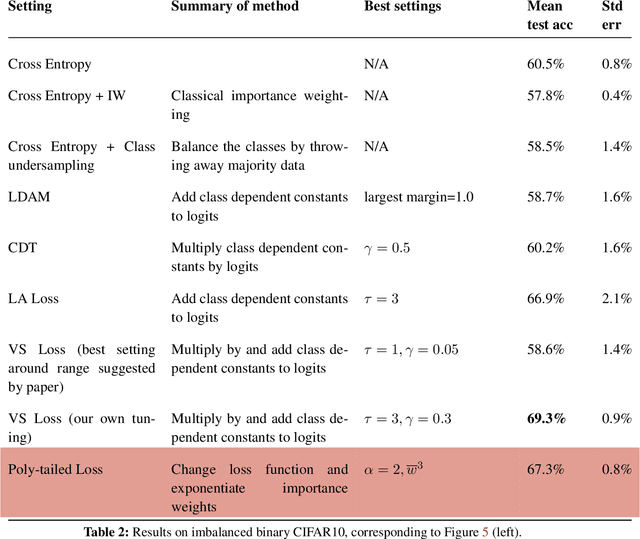
Importance weighting is a classic technique to handle distribution shifts. However, prior work has presented strong empirical and theoretical evidence demonstrating that importance weights can have little to no effect on overparameterized neural networks. Is importance weighting truly incompatible with the training of overparameterized neural networks? Our paper answers this in the negative. We show that importance weighting fails not because of the overparameterization, but instead, as a result of using exponentially-tailed losses like the logistic or cross-entropy loss. As a remedy, we show that polynomially-tailed losses restore the effects of importance reweighting in correcting distribution shift in overparameterized models. We characterize the behavior of gradient descent on importance weighted polynomially-tailed losses with overparameterized linear models, and theoretically demonstrate the advantage of using polynomially-tailed losses in a label shift setting. Surprisingly, our theory shows that using weights that are obtained by exponentiating the classical unbiased importance weights can improve performance. Finally, we demonstrate the practical value of our analysis with neural network experiments on a subpopulation shift and a label shift dataset. When reweighted, our loss function can outperform reweighted cross-entropy by as much as 9% in test accuracy. Our loss function also gives test accuracies comparable to, or even exceeding, well-tuned state-of-the-art methods for correcting distribution shifts.

GOPHER: Categorical probabilistic forecasting with graph structure via local continuous-time dynamics

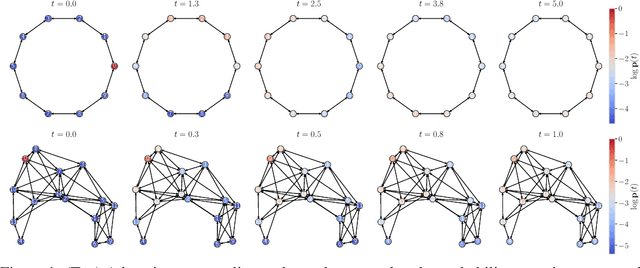
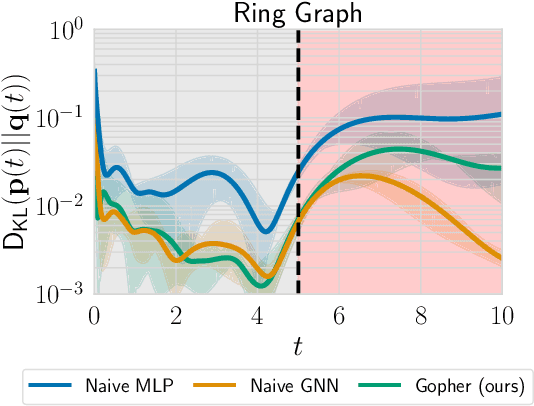
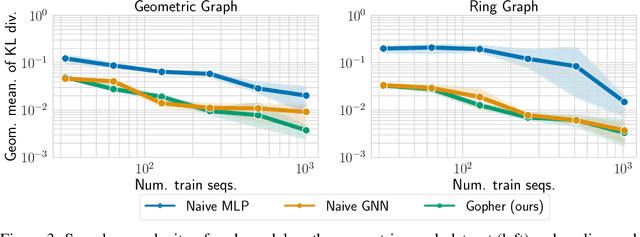
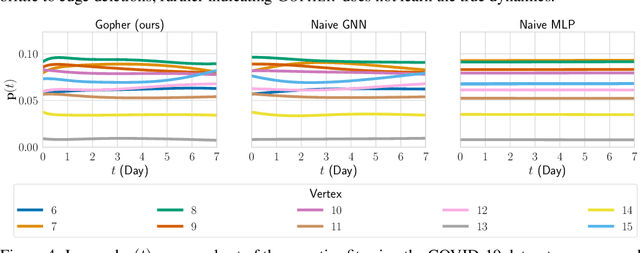
We consider the problem of probabilistic forecasting over categories with graph structure, where the dynamics at a vertex depends on its local connectivity structure. We present GOPHER, a method that combines the inductive bias of graph neural networks with neural ODEs to capture the intrinsic local continuous-time dynamics of our probabilistic forecasts. We study the benefits of these two inductive biases by comparing against baseline models that help disentangle the benefits of each. We find that capturing the graph structure is crucial for accurate in-domain probabilistic predictions and more sample efficient models. Surprisingly, our experiments demonstrate that the continuous time evolution inductive bias brings little to no benefit despite reflecting the true probability dynamics.

SKIing on Simplices: Kernel Interpolation on the Permutohedral Lattice for Scalable Gaussian Processes

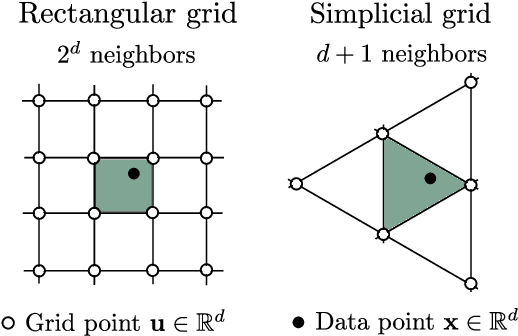
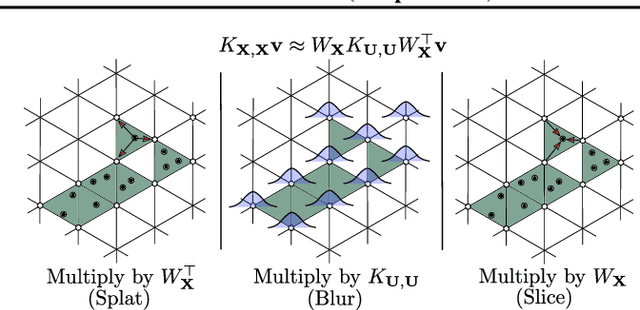
State-of-the-art methods for scalable Gaussian processes use iterative algorithms, requiring fast matrix vector multiplies (MVMs) with the covariance kernel. The Structured Kernel Interpolation (SKI) framework accelerates these MVMs by performing efficient MVMs on a grid and interpolating back to the original space. In this work, we develop a connection between SKI and the permutohedral lattice used for high-dimensional fast bilateral filtering. Using a sparse simplicial grid instead of a dense rectangular one, we can perform GP inference exponentially faster in the dimension than SKI. Our approach, Simplex-GP, enables scaling SKI to high dimensions, while maintaining strong predictive performance. We additionally provide a CUDA implementation of Simplex-GP, which enables significant GPU acceleration of MVM based inference.

Bayesian Algorithm Execution: Estimating Computable Properties of Black-box Functions Using Mutual Information

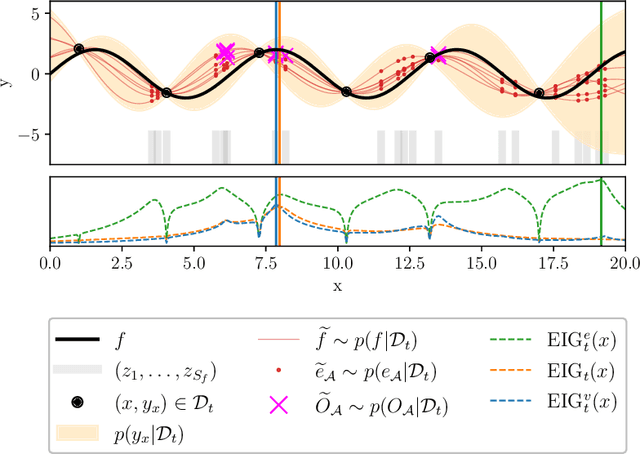
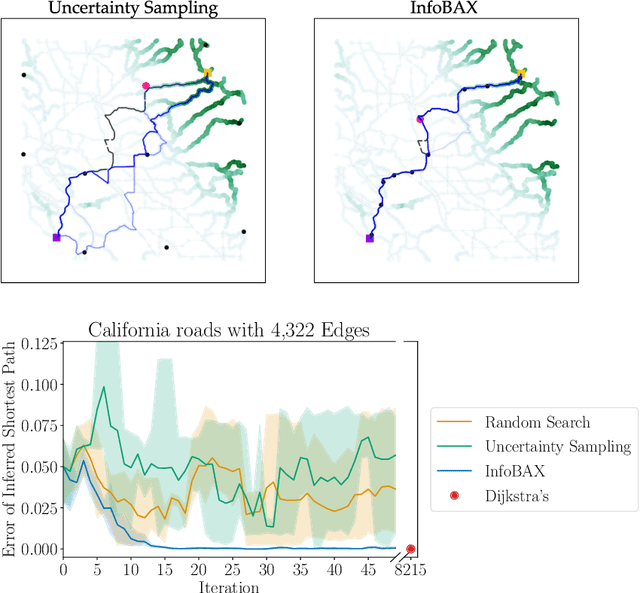
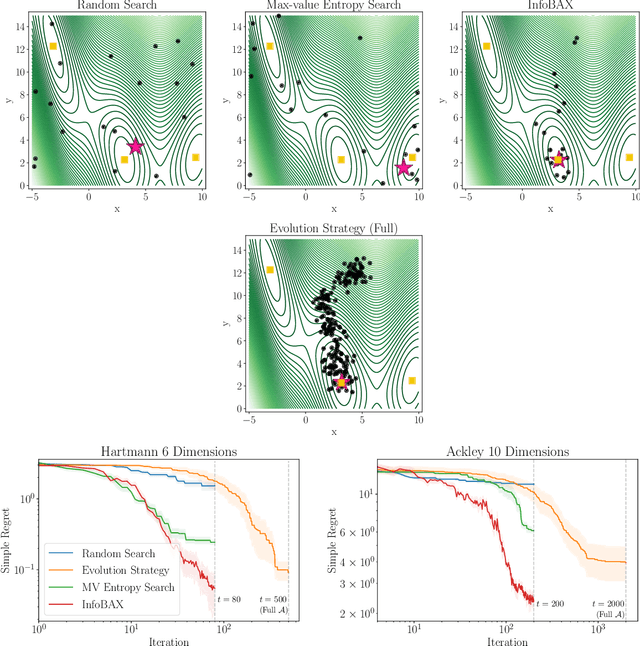
In many real world problems, we want to infer some property of an expensive black-box function f, given a budget of T function evaluations. One example is budget constrained global optimization of f, for which Bayesian optimization is a popular method. Other properties of interest include local optima, level sets, integrals, or graph-structured information induced by f. Often, we can find an algorithm A to compute the desired property, but it may require far more than T queries to execute. Given such an A, and a prior distribution over f, we refer to the problem of inferring the output of A using T evaluations as Bayesian Algorithm Execution (BAX). To tackle this problem, we present a procedure, InfoBAX, that sequentially chooses queries that maximize mutual information with respect to the algorithm's output. Applying this to Dijkstra's algorithm, for instance, we infer shortest paths in synthetic and real-world graphs with black-box edge costs. Using evolution strategies, we yield variants of Bayesian optimization that target local, rather than global, optima. On these problems, InfoBAX uses up to 500 times fewer queries to f than required by the original algorithm. Our method is closely connected to other Bayesian optimal experimental design procedures such as entropy search methods and optimal sensor placement using Gaussian processes.

Simplifying Hamiltonian and Lagrangian Neural Networks via Explicit Constraints

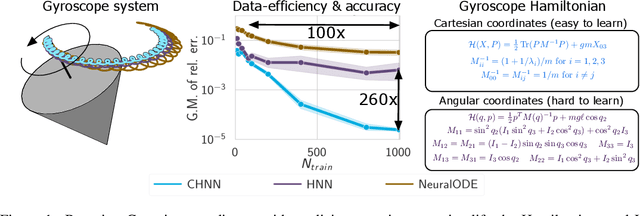
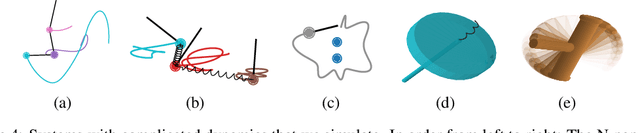
Reasoning about the physical world requires models that are endowed with the right inductive biases to learn the underlying dynamics. Recent works improve generalization for predicting trajectories by learning the Hamiltonian or Lagrangian of a system rather than the differential equations directly. While these methods encode the constraints of the systems using generalized coordinates, we show that embedding the system into Cartesian coordinates and enforcing the constraints explicitly with Lagrange multipliers dramatically simplifies the learning problem. We introduce a series of challenging chaotic and extended-body systems, including systems with N-pendulums, spring coupling, magnetic fields, rigid rotors, and gyroscopes, to push the limits of current approaches. Our experiments show that Cartesian coordinates with explicit constraints lead to a 100x improvement in accuracy and data efficiency.

$DC^2$: A Divide-and-conquer Algorithm for Large-scale Kernel Learning with Application to Clustering

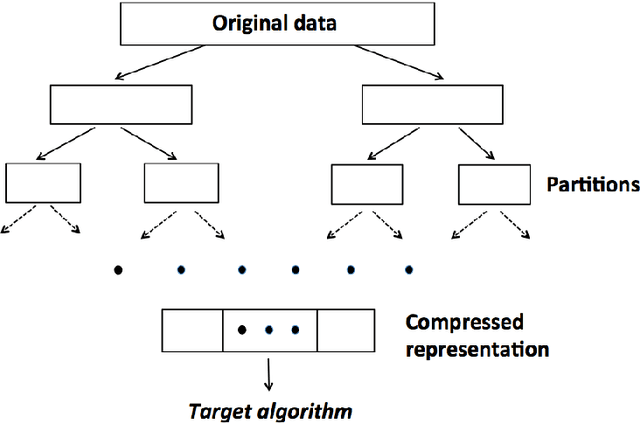
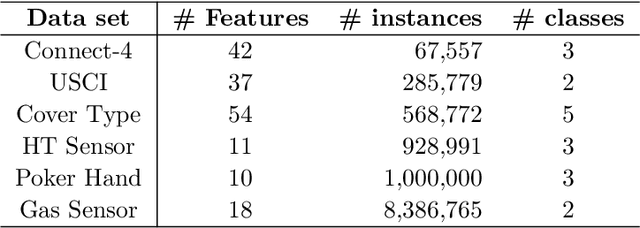
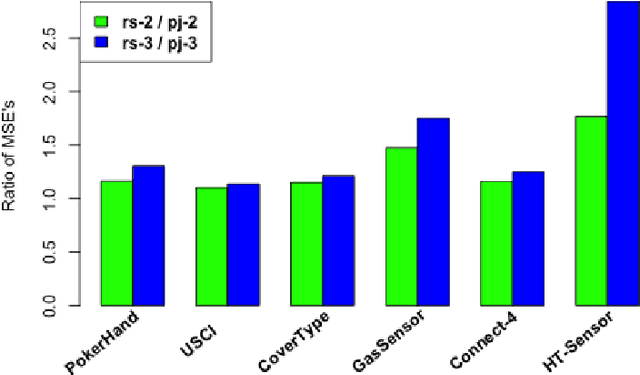
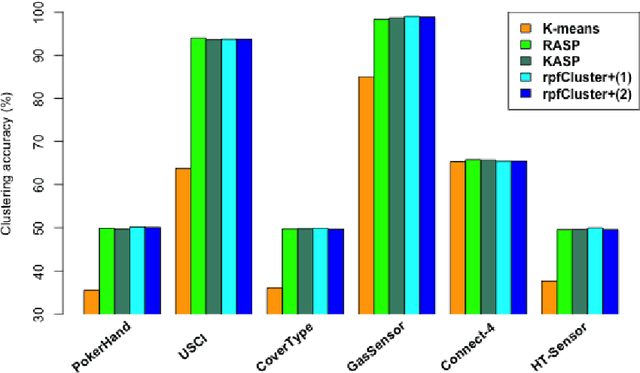
Divide-and-conquer is a general strategy to deal with large scale problems. It is typically applied to generate ensemble instances, which potentially limits the problem size it can handle. Additionally, the data are often divided by random sampling which may be suboptimal. To address these concerns, we propose the $DC^2$ algorithm. Instead of ensemble instances, we produce structure-preserving signature pieces to be assembled and conquered. $DC^2$ achieves the efficiency of sampling-based large scale kernel methods while enabling parallel multicore or clustered computation. The data partition and subsequent compression are unified by recursive random projections. Empirically dividing the data by random projections induces smaller mean squared approximation errors than conventional random sampling. The power of $DC^2$ is demonstrated by our clustering algorithm $rpfCluster^+$, which is as accurate as some fastest approximate spectral clustering algorithms while maintaining a running time close to that of K-means clustering. Analysis on $DC^2$ when applied to spectral clustering shows that the loss in clustering accuracy due to data division and reduction is upper bounded by the data approximation error which would vanish with recursive random projections. Due to its easy implementation and flexibility, we expect $DC^2$ to be applicable to general large scale learning problems.