Deep Linear Networks can Benignly Overfit when Shallow Ones Do

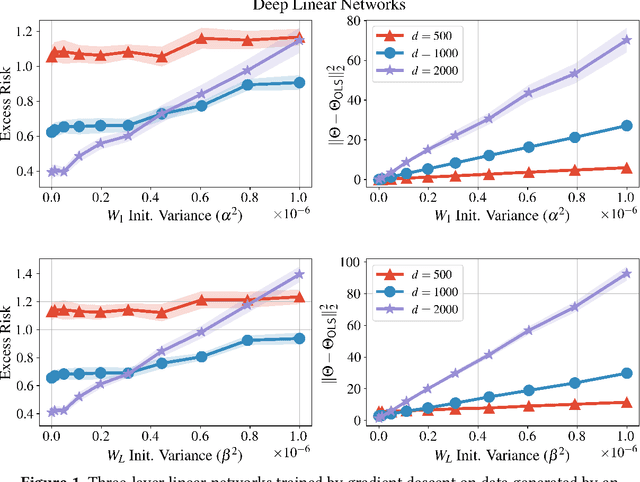
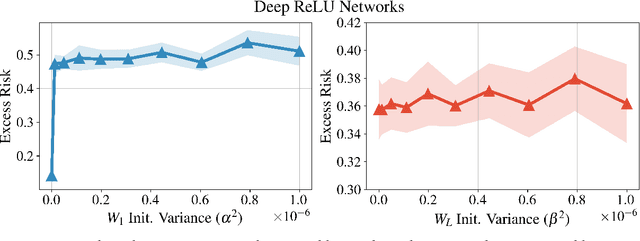
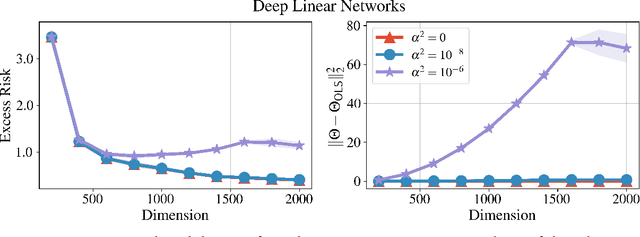
We bound the excess risk of interpolating deep linear networks trained using gradient flow. In a setting previously used to establish risk bounds for the minimum $\ell_2$-norm interpolant, we show that randomly initialized deep linear networks can closely approximate or even match known bounds for the minimum $\ell_2$-norm interpolant. Our analysis also reveals that interpolating deep linear models have exactly the same conditional variance as the minimum $\ell_2$-norm solution. Since the noise affects the excess risk only through the conditional variance, this implies that depth does not improve the algorithm's ability to "hide the noise". Our simulations verify that aspects of our bounds reflect typical behavior for simple data distributions. We also find that similar phenomena are seen in simulations with ReLU networks, although the situation there is more nuanced.

Undersampling is a Minimax Optimal Robustness Intervention in Nonparametric Classification

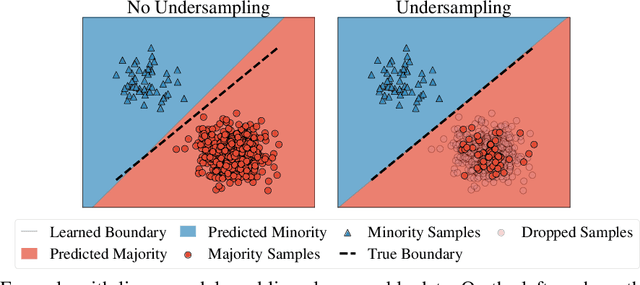
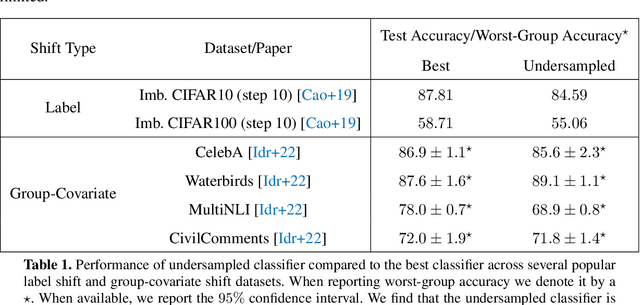
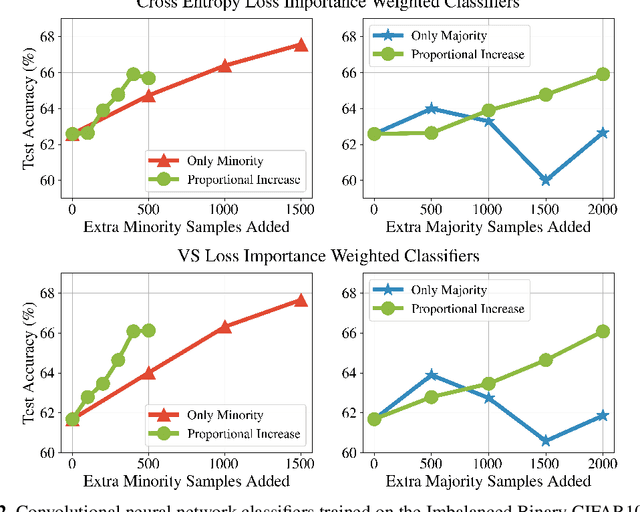
While a broad range of techniques have been proposed to tackle distribution shift, the simple baseline of training on an $\textit{undersampled}$ dataset often achieves close to state-of-the-art-accuracy across several popular benchmarks. This is rather surprising, since undersampling algorithms discard excess majority group data. To understand this phenomenon, we ask if learning is fundamentally constrained by a lack of minority group samples. We prove that this is indeed the case in the setting of nonparametric binary classification. Our results show that in the worst case, an algorithm cannot outperform undersampling unless there is a high degree of overlap between the train and test distributions (which is unlikely to be the case in real-world datasets), or if the algorithm leverages additional structure about the distribution shift. In particular, in the case of label shift we show that there is always an undersampling algorithm that is minimax optimal. While in the case of group-covariate shift we show that there is an undersampling algorithm that is minimax optimal when the overlap between the group distributions is small. We also perform an experimental case study on a label shift dataset and find that in line with our theory the test accuracy of robust neural network classifiers is constrained by the number of minority samples.

Random Feature Amplification: Feature Learning and Generalization in Neural Networks

In this work, we provide a characterization of the feature-learning process in two-layer ReLU networks trained by gradient descent on the logistic loss following random initialization. We consider data with binary labels that are generated by an XOR-like function of the input features. We permit a constant fraction of the training labels to be corrupted by an adversary. We show that, although linear classifiers are no better than random guessing for the distribution we consider, two-layer ReLU networks trained by gradient descent achieve generalization error close to the label noise rate, refuting the conjecture of Malach and Shalev-Shwartz that 'deeper is better only when shallow is good'. We develop a novel proof technique that shows that at initialization, the vast majority of neurons function as random features that are only weakly correlated with useful features, and the gradient descent dynamics 'amplify' these weak, random features to strong, useful features.

Benign Overfitting without Linearity: Neural Network Classifiers Trained by Gradient Descent for Noisy Linear Data

Benign overfitting, the phenomenon where interpolating models generalize well in the presence of noisy data, was first observed in neural network models trained with gradient descent. To better understand this empirical observation, we consider the generalization error of two-layer neural networks trained to interpolation by gradient descent on the logistic loss following random initialization. We assume the data comes from well-separated class-conditional log-concave distributions and allow for a constant fraction of the training labels to be corrupted by an adversary. We show that in this setting, neural networks exhibit benign overfitting: they can be driven to zero training error, perfectly fitting any noisy training labels, and simultaneously achieve test error close to the Bayes-optimal error. In contrast to previous work on benign overfitting that require linear or kernel-based predictors, our analysis holds in a setting where both the model and learning dynamics are fundamentally nonlinear.

Is Importance Weighting Incompatible with Interpolating Classifiers?

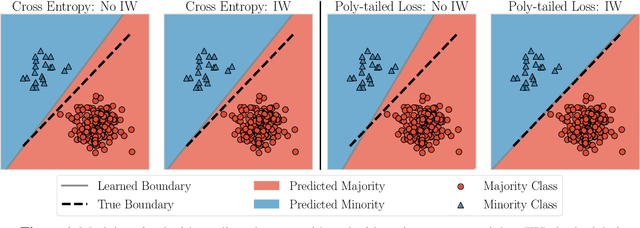
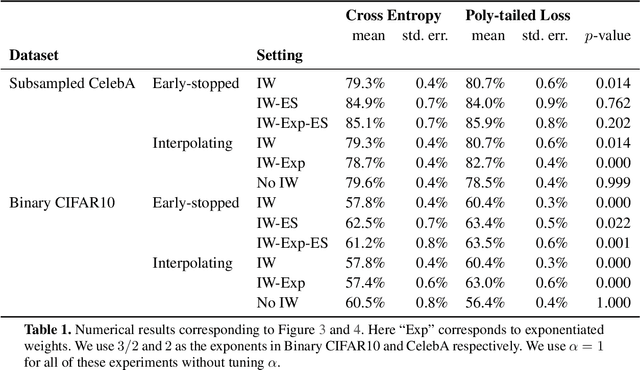
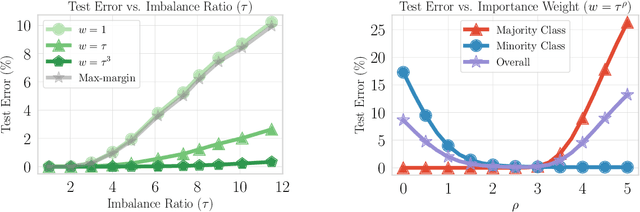
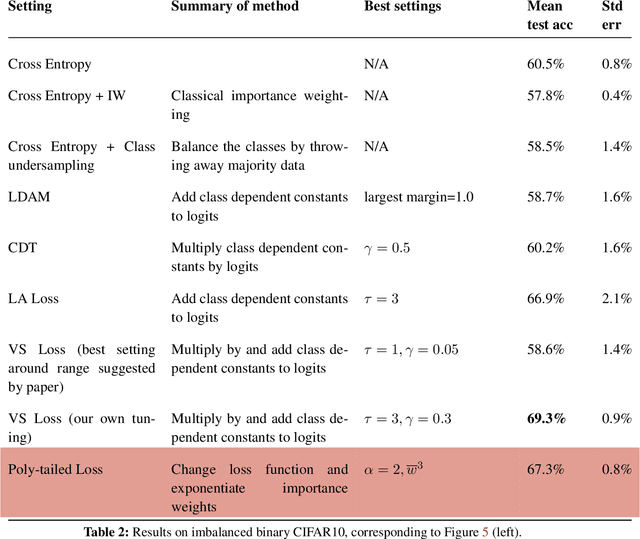
Importance weighting is a classic technique to handle distribution shifts. However, prior work has presented strong empirical and theoretical evidence demonstrating that importance weights can have little to no effect on overparameterized neural networks. Is importance weighting truly incompatible with the training of overparameterized neural networks? Our paper answers this in the negative. We show that importance weighting fails not because of the overparameterization, but instead, as a result of using exponentially-tailed losses like the logistic or cross-entropy loss. As a remedy, we show that polynomially-tailed losses restore the effects of importance reweighting in correcting distribution shift in overparameterized models. We characterize the behavior of gradient descent on importance weighted polynomially-tailed losses with overparameterized linear models, and theoretically demonstrate the advantage of using polynomially-tailed losses in a label shift setting. Surprisingly, our theory shows that using weights that are obtained by exponentiating the classical unbiased importance weights can improve performance. Finally, we demonstrate the practical value of our analysis with neural network experiments on a subpopulation shift and a label shift dataset. When reweighted, our loss function can outperform reweighted cross-entropy by as much as 9% in test accuracy. Our loss function also gives test accuracies comparable to, or even exceeding, well-tuned state-of-the-art methods for correcting distribution shifts.

Foolish Crowds Support Benign Overfitting

We prove a lower bound on the excess risk of sparse interpolating procedures for linear regression with Gaussian data in the overparameterized regime. We apply this result to obtain a lower bound for basis pursuit (the minimum $\ell_1$-norm interpolant) that implies that its excess risk can converge at an exponentially slower rate than OLS (the minimum $\ell_2$-norm interpolant), even when the ground truth is sparse. Our analysis exposes the benefit of an effect analogous to the "wisdom of the crowd", except here the harm arising from fitting the noise is ameliorated by spreading it among many directions - the variance reduction arises from a foolish crowd.

The Interplay Between Implicit Bias and Benign Overfitting in Two-Layer Linear Networks

The recent success of neural network models has shone light on a rather surprising statistical phenomenon: statistical models that perfectly fit noisy data can generalize well to unseen test data. Understanding this phenomenon of $\textit{benign overfitting}$ has attracted intense theoretical and empirical study. In this paper, we consider interpolating two-layer linear neural networks trained with gradient flow on the squared loss and derive bounds on the excess risk when the covariates satisfy sub-Gaussianity and anti-concentration properties, and the noise is independent and sub-Gaussian. By leveraging recent results that characterize the implicit bias of this estimator, our bounds emphasize the role of both the quality of the initialization as well as the properties of the data covariance matrix in achieving low excess risk.

On the Theory of Reinforcement Learning with Once-per-Episode Feedback

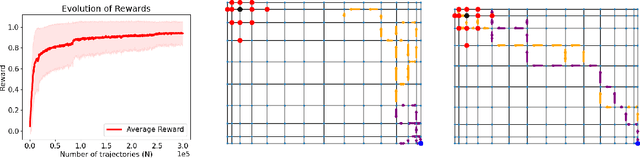
We study a theory of reinforcement learning (RL) in which the learner receives binary feedback only once at the end of an episode. While this is an extreme test case for theory, it is also arguably more representative of real-world applications than the traditional requirement in RL practice that the learner receive feedback at every time step. Indeed, in many real-world applications of reinforcement learning, such as self-driving cars and robotics, it is easier to evaluate whether a learner's complete trajectory was either "good" or "bad," but harder to provide a reward signal at each step. To show that learning is possible in this more challenging setting, we study the case where trajectory labels are generated by an unknown parametric model, and provide a statistically and computationally efficient algorithm that achieves sub-linear regret.

When does gradient descent with logistic loss interpolate using deep networks with smoothed ReLU activations?

We establish conditions under which gradient descent applied to fixed-width deep networks drives the logistic loss to zero, and prove bounds on the rate of convergence. Our analysis applies for smoothed approximations to the ReLU, such as Swish and the Huberized ReLU, proposed in previous applied work. We provide two sufficient conditions for convergence. The first is simply a bound on the loss at initialization. The second is a data separation condition used in prior analyses.

When does gradient descent with logistic loss find interpolating two-layer networks?

We study the training of finite-width two-layer smoothed ReLU networks for binary classification using the logistic loss. We show that gradient descent drives the training loss to zero if the initial loss is small enough. When the data satisfies certain cluster and separation conditions and the network is wide enough, we show that one step of gradient descent reduces the loss sufficiently that the first result applies. In contrast, all past analyses of fixed-width networks that we know do not guarantee that the training loss goes to zero.