Matrix Cofactorization for Joint Representation Learning and Supervised Classification -- Application to Hyperspectral Image Analysis

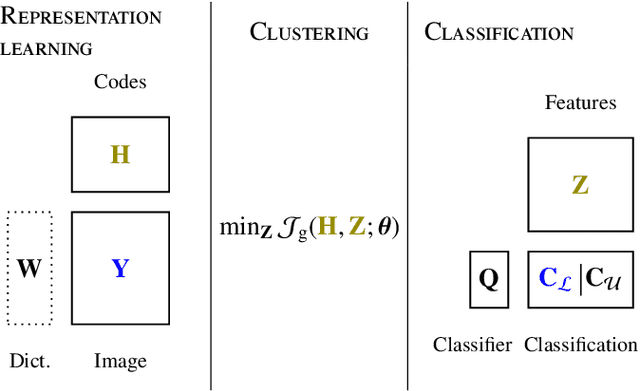
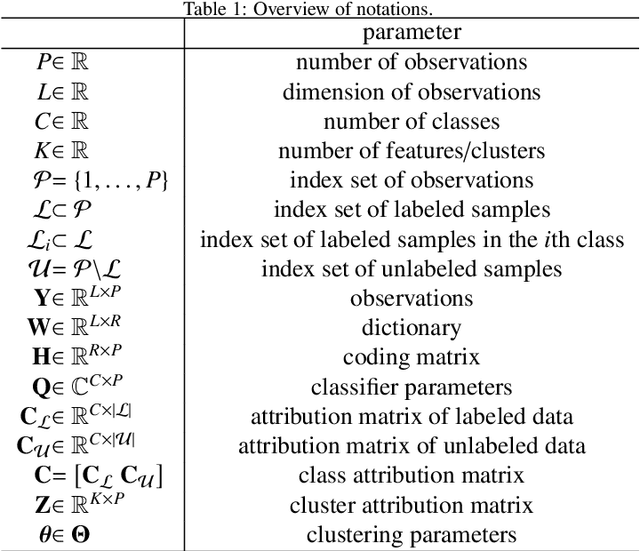
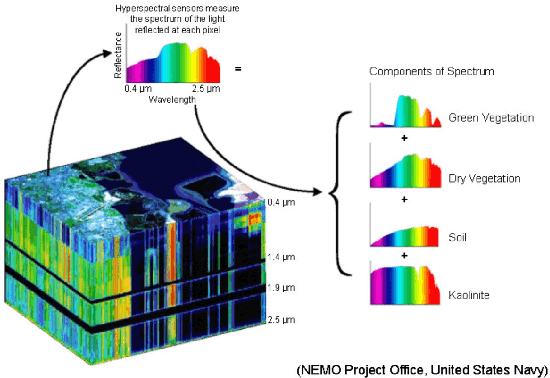
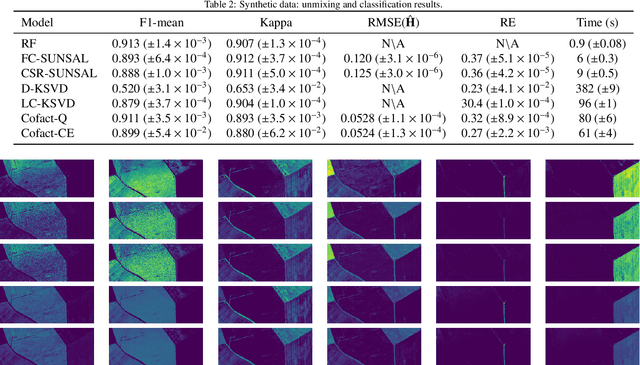
Supervised classification and representation learning are two widely used methods to analyze multivariate images. Although complementary, these two classes of methods have been scarcely considered jointly. In this paper, a method coupling these two approaches is designed using a matrix cofactorization formulation. Each task is modeled as a factorization matrix problem and a term relating both coding matrices is then introduced to drive an appropriate coupling. The link can be interpreted as a clustering operation over the low-dimensional representation vectors. The attribution vectors of the clustering are then used as features vectors for the classification task, i.e., the coding vectors of the corresponding factorization problem. A proximal gradient descent algorithm, ensuring convergence to a critical point of the objective function, is then derived to solve the resulting non-convex non-smooth optimization problem. An evaluation of the proposed method is finally conducted both on synthetic and real data in the specific context of hyperspectral image interpretation, unifying two standard analysis techniques, namely unmixing and classification.

Super-resolution of Sentinel-2 images: Learning a globally applicable deep neural network

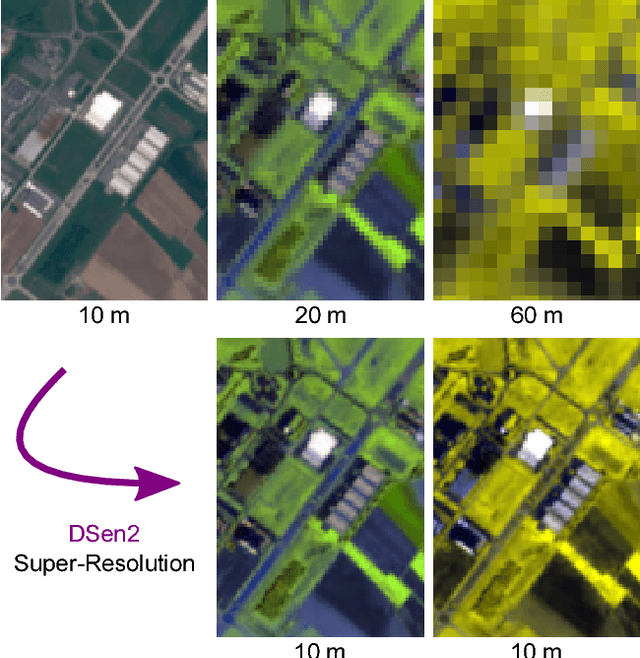
The Sentinel-2 satellite mission delivers multi-spectral imagery with 13 spectral bands, acquired at three different spatial resolutions. The aim of this research is to super-resolve the lower-resolution (20 m and 60 m Ground Sampling Distance - GSD) bands to 10 m GSD, so as to obtain a complete data cube at the maximal sensor resolution. We employ a state-of-the-art convolutional neural network (CNN) to perform end-to-end upsampling, which is trained with data at lower resolution, i.e., from 40->20 m, respectively 360->60 m GSD. In this way, one has access to a virtually infinite amount of training data, by downsampling real Sentinel-2 images. We use data sampled globally over a wide range of geographical locations, to obtain a network that generalises across different climate zones and land-cover types, and can super-resolve arbitrary Sentinel-2 images without the need of retraining. In quantitative evaluations (at lower scale, where ground truth is available), our network, which we call DSen2, outperforms the best competing approach by almost 50% in RMSE, while better preserving the spectral characteristics. It also delivers visually convincing results at the full 10 m GSD. The code is available at https://github.com/lanha/DSen2

An Extension of Averaged-Operator-Based Algorithms

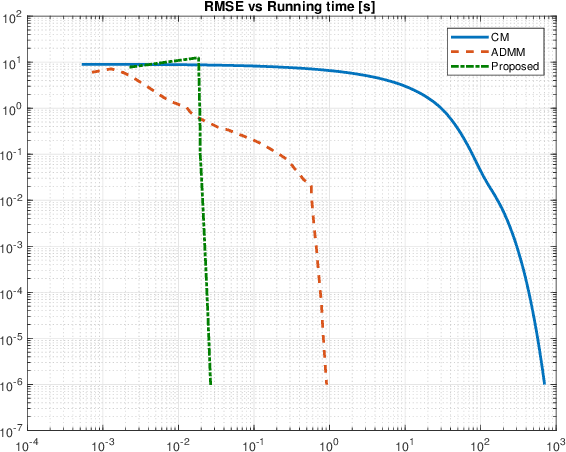
Many of the algorithms used to solve minimization problems with sparsity-inducing regularizers are generic in the sense that they do not take into account the sparsity of the solution in any particular way. However, algorithms known as semismooth Newton are able to take advantage of this sparsity to accelerate their convergence. We show how to extend these algorithms in different directions, and study the convergence of the resulting algorithms by showing that they are a particular case of an extension of the well-known Krasnosel'ski\u{\i}--Mann scheme.

Restoring STM images via Sparse Coding: noise and artifact removal

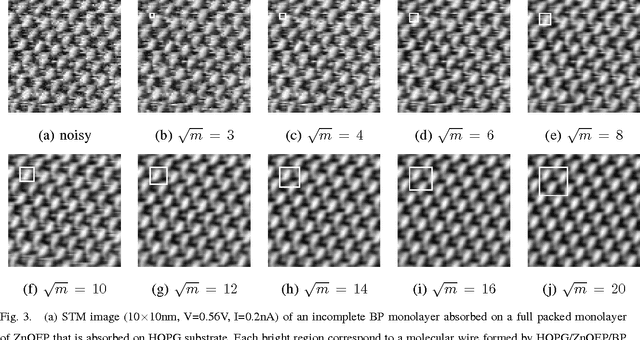
In this article, we present a denoising algorithm to improve the interpretation and quality of scanning tunneling microscopy (STM) images. Given the high level of self-similarity of STM images, we propose a denoising algorithm by reformulating the true estimation problem as a sparse regression, often termed sparse coding. We introduce modifications to the algorithm to cope with the existence of artifacts, mainly dropouts, which appear in a structured way as consecutive line segments on the scanning direction. The resulting algorithm treats the artifacts as missing data, and the estimated values outperform those algorithms that substitute the outliers by a local filtering. We provide code implementations for both Matlab and Gwyddion.

A Framework for Fast Image Deconvolution with Incomplete Observations

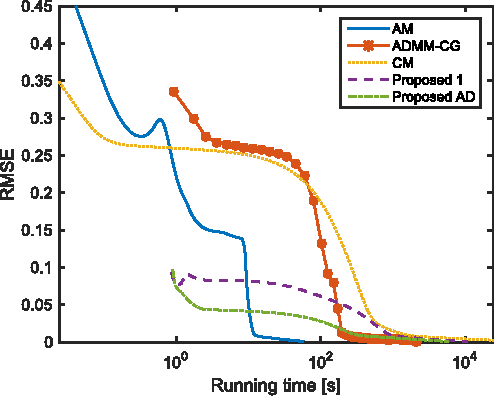
In image deconvolution problems, the diagonalization of the underlying operators by means of the FFT usually yields very large speedups. When there are incomplete observations (e.g., in the case of unknown boundaries), standard deconvolution techniques normally involve non-diagonalizable operators, resulting in rather slow methods, or, otherwise, use inexact convolution models, resulting in the occurrence of artifacts in the enhanced images. In this paper, we propose a new deconvolution framework for images with incomplete observations that allows us to work with diagonalized convolution operators, and therefore is very fast. We iteratively alternate the estimation of the unknown pixels and of the deconvolved image, using, e.g., an FFT-based deconvolution method. This framework is an efficient, high-quality alternative to existing methods of dealing with the image boundaries, such as edge tapering. It can be used with any fast deconvolution method. We give an example in which a state-of-the-art method that assumes periodic boundary conditions is extended, through the use of this framework, to unknown boundary conditions. Furthermore, we propose a specific implementation of this framework, based on the alternating direction method of multipliers (ADMM). We provide a proof of convergence for the resulting algorithm, which can be seen as a "partial" ADMM, in which not all variables are dualized. We report experimental comparisons with other primal-dual methods, where the proposed one performed at the level of the state of the art. Four different kinds of applications were tested in the experiments: deconvolution, deconvolution with inpainting, superresolution, and demosaicing, all with unknown boundaries.

Image Classification with Rejection using Contextual Information

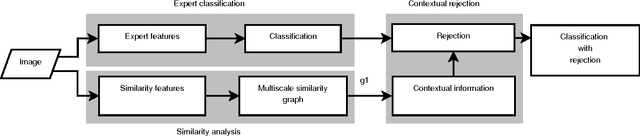
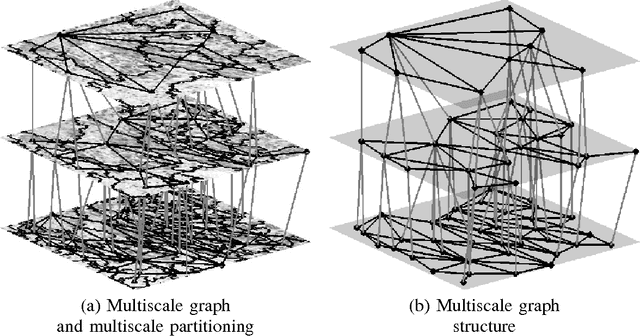
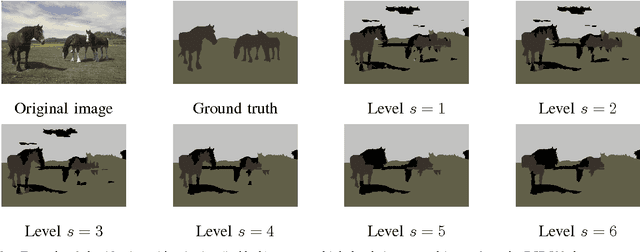
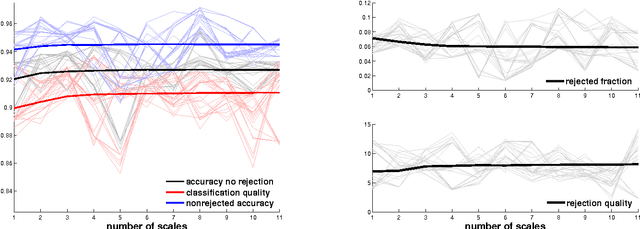
We introduce a new supervised algorithm for image classification with rejection using multiscale contextual information. Rejection is desired in image-classification applications that require a robust classifier but not the classification of the entire image. The proposed algorithm combines local and multiscale contextual information with rejection, improving the classification performance. As a probabilistic model for classification, we adopt a multinomial logistic regression. The concept of rejection with contextual information is implemented by modeling the classification problem as an energy minimization problem over a graph representing local and multiscale similarities of the image. The rejection is introduced through an energy data term associated with the classification risk and the contextual information through an energy smoothness term associated with the local and multiscale similarities within the image. We illustrate the proposed method on the classification of images of H&E-stained teratoma tissues.

Semiblind Hyperspectral Unmixing in the Presence of Spectral Library Mismatches

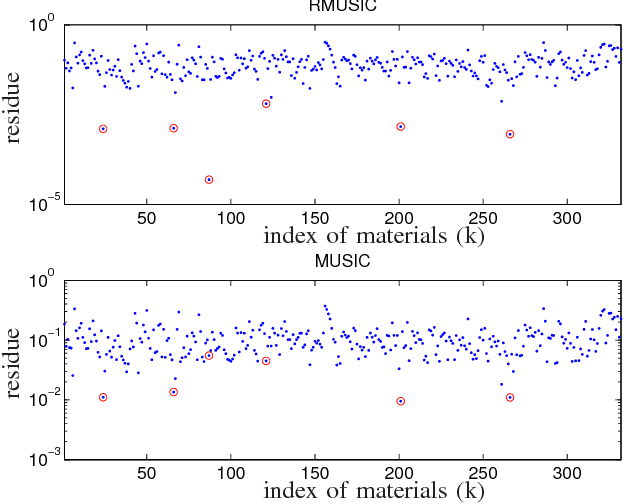
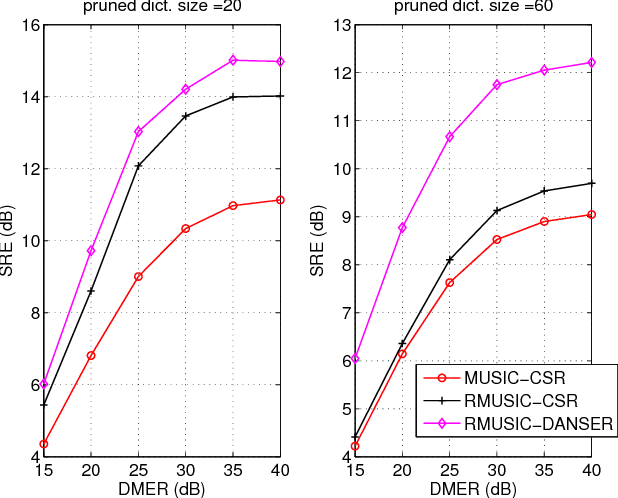
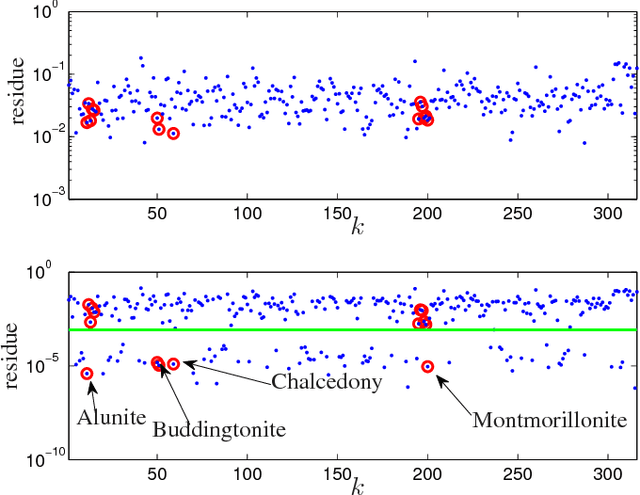
The dictionary-aided sparse regression (SR) approach has recently emerged as a promising alternative to hyperspectral unmixing (HU) in remote sensing. By using an available spectral library as a dictionary, the SR approach identifies the underlying materials in a given hyperspectral image by selecting a small subset of spectral samples in the dictionary to represent the whole image. A drawback with the current SR developments is that an actual spectral signature in the scene is often assumed to have zero mismatch with its corresponding dictionary sample, and such an assumption is considered too ideal in practice. In this paper, we tackle the spectral signature mismatch problem by proposing a dictionary-adjusted nonconvex sparsity-encouraging regression (DANSER) framework. The main idea is to incorporate dictionary correcting variables in an SR formulation. A simple and low per-iteration complexity algorithm is tailor-designed for practical realization of DANSER. Using the same dictionary correcting idea, we also propose a robust subspace solution for dictionary pruning. Extensive simulations and real-data experiments show that the proposed method is effective in mitigating the undesirable spectral signature mismatch effects.

A convex formulation for hyperspectral image superresolution via subspace-based regularization

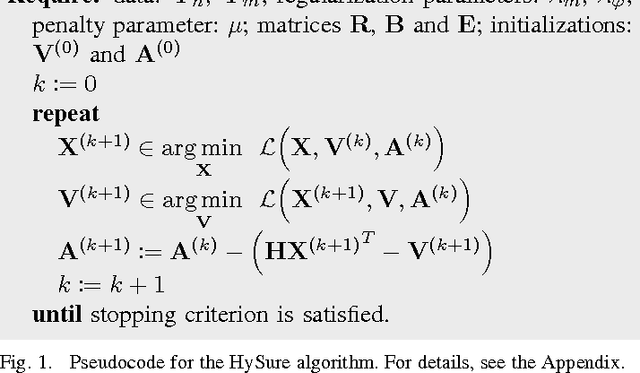
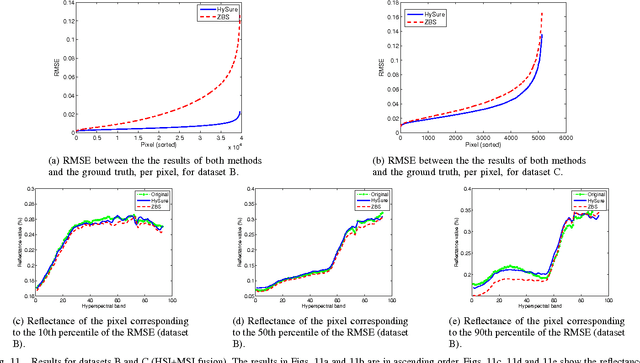
Hyperspectral remote sensing images (HSIs) usually have high spectral resolution and low spatial resolution. Conversely, multispectral images (MSIs) usually have low spectral and high spatial resolutions. The problem of inferring images which combine the high spectral and high spatial resolutions of HSIs and MSIs, respectively, is a data fusion problem that has been the focus of recent active research due to the increasing availability of HSIs and MSIs retrieved from the same geographical area. We formulate this problem as the minimization of a convex objective function containing two quadratic data-fitting terms and an edge-preserving regularizer. The data-fitting terms account for blur, different resolutions, and additive noise. The regularizer, a form of vector Total Variation, promotes piecewise-smooth solutions with discontinuities aligned across the hyperspectral bands. The downsampling operator accounting for the different spatial resolutions, the non-quadratic and non-smooth nature of the regularizer, and the very large size of the HSI to be estimated lead to a hard optimization problem. We deal with these difficulties by exploiting the fact that HSIs generally "live" in a low-dimensional subspace and by tailoring the Split Augmented Lagrangian Shrinkage Algorithm (SALSA), which is an instance of the Alternating Direction Method of Multipliers (ADMM), to this optimization problem, by means of a convenient variable splitting. The spatial blur and the spectral linear operators linked, respectively, with the HSI and MSI acquisition processes are also estimated, and we obtain an effective algorithm that outperforms the state-of-the-art, as illustrated in a series of experiments with simulated and real-life data.

Hyperspectral and Multispectral Image Fusion based on a Sparse Representation

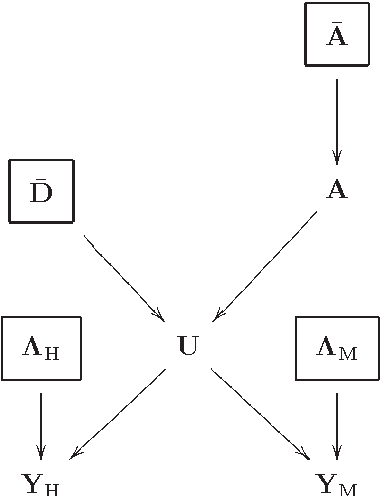
This paper presents a variational based approach to fusing hyperspectral and multispectral images. The fusion process is formulated as an inverse problem whose solution is the target image assumed to live in a much lower dimensional subspace. A sparse regularization term is carefully designed, relying on a decomposition of the scene on a set of dictionaries. The dictionary atoms and the corresponding supports of active coding coefficients are learned from the observed images. Then, conditionally on these dictionaries and supports, the fusion problem is solved via alternating optimization with respect to the target image (using the alternating direction method of multipliers) and the coding coefficients. Simulation results demonstrate the efficiency of the proposed algorithm when compared with the state-of-the-art fusion methods.

Hyperspectral image superresolution: An edge-preserving convex formulation

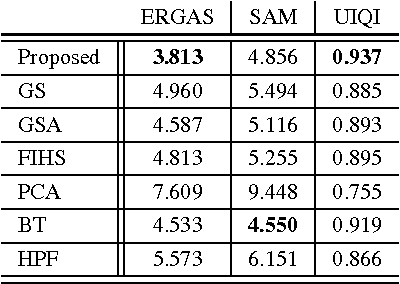
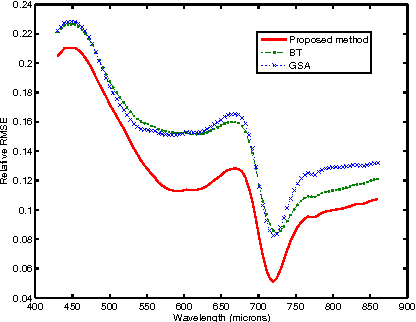
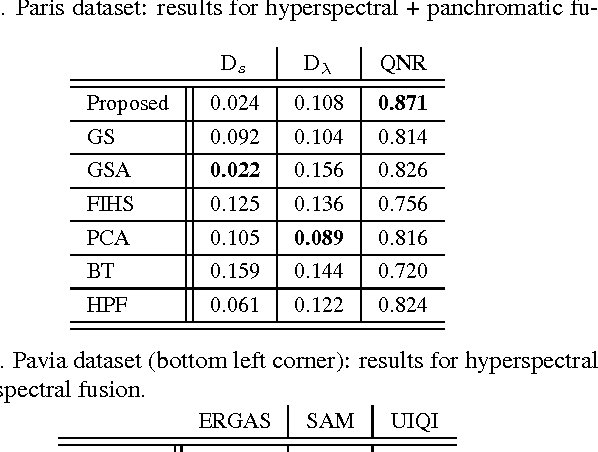
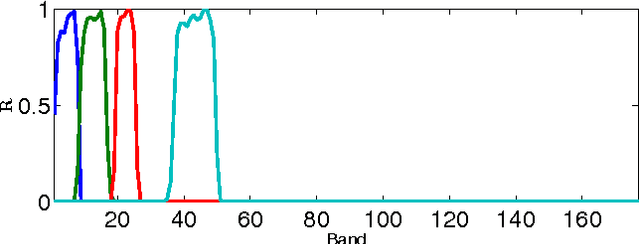
Hyperspectral remote sensing images (HSIs) are characterized by having a low spatial resolution and a high spectral resolution, whereas multispectral images (MSIs) are characterized by low spectral and high spatial resolutions. These complementary characteristics have stimulated active research in the inference of images with high spatial and spectral resolutions from HSI-MSI pairs. In this paper, we formulate this data fusion problem as the minimization of a convex objective function containing two data-fitting terms and an edge-preserving regularizer. The data-fitting terms are quadratic and account for blur, different spatial resolutions, and additive noise; the regularizer, a form of vector Total Variation, promotes aligned discontinuities across the reconstructed hyperspectral bands. The optimization described above is rather hard, owing to its non-diagonalizable linear operators, to the non-quadratic and non-smooth nature of the regularizer, and to the very large size of the image to be inferred. We tackle these difficulties by tailoring the Split Augmented Lagrangian Shrinkage Algorithm (SALSA)---an instance of the Alternating Direction Method of Multipliers (ADMM)---to this optimization problem. By using a convenient variable splitting and by exploiting the fact that HSIs generally "live" in a low-dimensional subspace, we obtain an effective algorithm that yields state-of-the-art results, as illustrated by experiments.