NeurIPS 2023 Competition: Privacy Preserving Federated Learning Document VQA

The Privacy Preserving Federated Learning Document VQA (PFL-DocVQA) competition challenged the community to develop provably private and communication-efficient solutions in a federated setting for a real-life use case: invoice processing. The competition introduced a dataset of real invoice documents, along with associated questions and answers requiring information extraction and reasoning over the document images. Thereby, it brings together researchers and expertise from the document analysis, privacy, and federated learning communities. Participants fine-tuned a pre-trained, state-of-the-art Document Visual Question Answering model provided by the organizers for this new domain, mimicking a typical federated invoice processing setup. The base model is a multi-modal generative language model, and sensitive information could be exposed through either the visual or textual input modality. Participants proposed elegant solutions to reduce communication costs while maintaining a minimum utility threshold in track 1 and to protect all information from each document provider using differential privacy in track 2. The competition served as a new testbed for developing and testing private federated learning methods, simultaneously raising awareness about privacy within the document image analysis and recognition community. Ultimately, the competition analysis provides best practices and recommendations for successfully running privacy-focused federated learning challenges in the future.

Noise-Aware Differentially Private Variational Inference

Differential privacy (DP) provides robust privacy guarantees for statistical inference, but this can lead to unreliable results and biases in downstream applications. While several noise-aware approaches have been proposed which integrate DP perturbation into the inference, they are limited to specific types of simple probabilistic models. In this work, we propose a novel method for noise-aware approximate Bayesian inference based on stochastic gradient variational inference which can also be applied to high-dimensional and non-conjugate models. We also propose a more accurate evaluation method for noise-aware posteriors. Empirically, our inference method has similar performance to existing methods in the domain where they are applicable. Outside this domain, we obtain accurate coverages on high-dimensional Bayesian linear regression and well-calibrated predictive probabilities on Bayesian logistic regression with the UCI Adult dataset.

Understanding Practical Membership Privacy of Deep Learning

We apply a state-of-the-art membership inference attack (MIA) to systematically test the practical privacy vulnerability of fine-tuning large image classification models.We focus on understanding the properties of data sets and samples that make them vulnerable to membership inference. In terms of data set properties, we find a strong power law dependence between the number of examples per class in the data and the MIA vulnerability, as measured by true positive rate of the attack at a low false positive rate. For an individual sample, large gradients at the end of training are strongly correlated with MIA vulnerability.

Subsampling is not Magic: Why Large Batch Sizes Work for Differentially Private Stochastic Optimisation

We study the effect of the batch size to the total gradient variance in differentially private stochastic gradient descent (DP-SGD), seeking a theoretical explanation for the usefulness of large batch sizes. As DP-SGD is the basis of modern DP deep learning, its properties have been widely studied, and recent works have empirically found large batch sizes to be beneficial. However, theoretical explanations of this benefit are currently heuristic at best. We first observe that the total gradient variance in DP-SGD can be decomposed into subsampling-induced and noise-induced variances. We then prove that in the limit of an infinite number of iterations, the effective noise-induced variance is invariant to the batch size. The remaining subsampling-induced variance decreases with larger batch sizes, so large batches reduce the effective total gradient variance. We confirm numerically that the asymptotic regime is relevant in practical settings when the batch size is not small, and find that outside the asymptotic regime, the total gradient variance decreases even more with large batch sizes. We also find a sufficient condition that implies that large batch sizes similarly reduce effective DP noise variance for one iteration of DP-SGD.

Collaborative Learning From Distributed Data With Differentially Private Synthetic Twin Data

Consider a setting where multiple parties holding sensitive data aim to collaboratively learn population level statistics, but pooling the sensitive data sets is not possible. We propose a framework in which each party shares a differentially private synthetic twin of their data. We study the feasibility of combining such synthetic twin data sets for collaborative learning on real-world health data from the UK Biobank. We discover that parties engaging in the collaborative learning via shared synthetic data obtain more accurate estimates of target statistics compared to using only their local data. This finding extends to the difficult case of small heterogeneous data sets. Furthermore, the more parties participate, the larger and more consistent the improvements become. Finally, we find that data sharing can especially help parties whose data contain underrepresented groups to perform better-adjusted analysis for said groups. Based on our results we conclude that sharing of synthetic twins is a viable method for enabling learning from sensitive data without violating privacy constraints even if individual data sets are small or do not represent the overall population well. The setting of distributed sensitive data is often a bottleneck in biomedical research, which our study shows can be alleviated with privacy-preserving collaborative learning methods.

DPVIm: Differentially Private Variational Inference Improved

Differentially private (DP) release of multidimensional statistics typically considers an aggregate sensitivity, e.g. the vector norm of a high-dimensional vector. However, different dimensions of that vector might have widely different magnitudes and therefore DP perturbation disproportionately affects the signal across dimensions. We observe this problem in the gradient release of the DP-SGD algorithm when using it for variational inference (VI), where it manifests in poor convergence as well as high variance in outputs for certain variational parameters, and make the following contributions: (i) We mathematically isolate the cause for the difference in magnitudes between gradient parts corresponding to different variational parameters. Using this as prior knowledge we establish a link between the gradients of the variational parameters, and propose an efficient while simple fix for the problem to obtain a less noisy gradient estimator, which we call $\textit{aligned}$ gradients. This approach allows us to obtain the updates for the covariance parameter of a Gaussian posterior approximation without a privacy cost. We compare this to alternative approaches for scaling the gradients using analytically derived preconditioning, e.g. natural gradients. (ii) We suggest using iterate averaging over the DP parameter traces recovered during the training, to reduce the DP-induced noise in parameter estimates at no additional cost in privacy. Finally, (iii) to accurately capture the additional uncertainty DP introduces to the model parameters, we infer the DP-induced noise from the parameter traces and include that in the learned posteriors to make them $\textit{noise aware}$. We demonstrate the efficacy of our proposed improvements through various experiments on real data.

Noise-Aware Statistical Inference with Differentially Private Synthetic Data

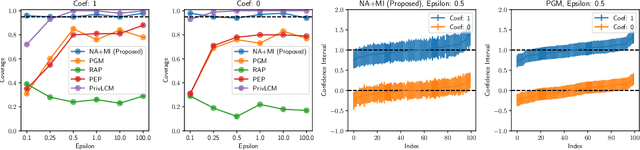
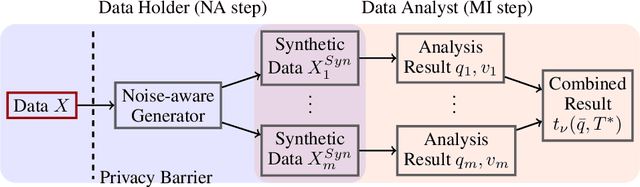
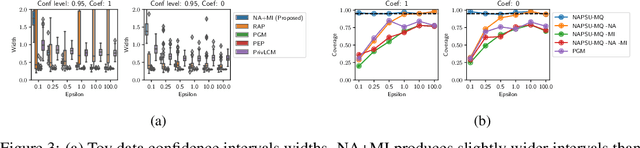
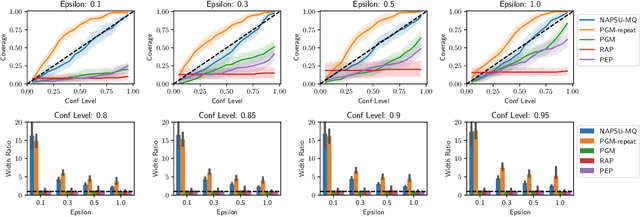
While generation of synthetic data under differential privacy (DP) has received a lot of attention in the data privacy community, analysis of synthetic data has received much less. Existing work has shown that simply analysing DP synthetic data as if it were real does not produce valid inferences of population-level quantities. For example, confidence intervals become too narrow, which we demonstrate with a simple experiment. We tackle this problem by combining synthetic data analysis techniques from the field of multiple imputation, and synthetic data generation using noise-aware Bayesian modeling into a pipeline NA+MI that allows computing accurate uncertainty estimates for population-level quantities from DP synthetic data. To implement NA+MI for discrete data generation from marginal queries, we develop a novel noise-aware synthetic data generation algorithm NAPSU-MQ using the principle of maximum entropy. Our experiments demonstrate that the pipeline is able to produce accurate confidence intervals from DP synthetic data. The intervals become wider with tighter privacy to accurately capture the additional uncertainty stemming from DP noise.

Locally Differentially Private Bayesian Inference

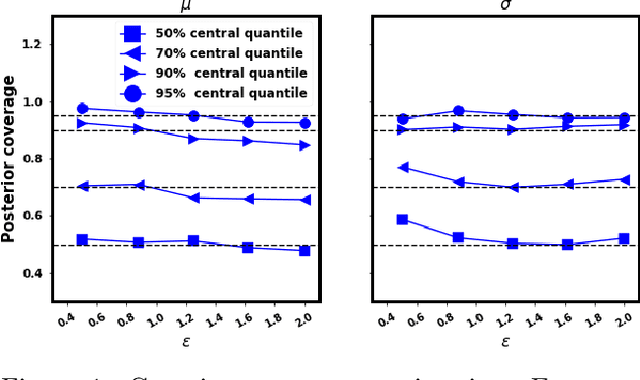
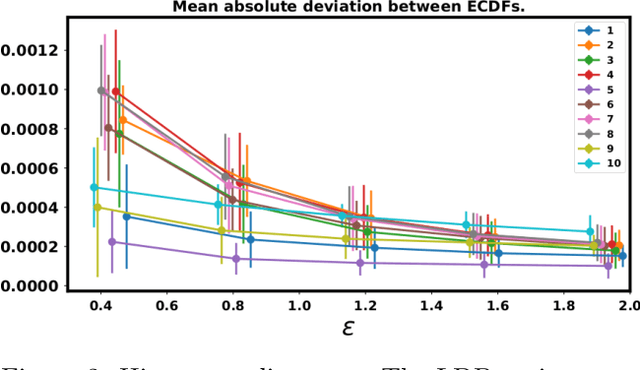
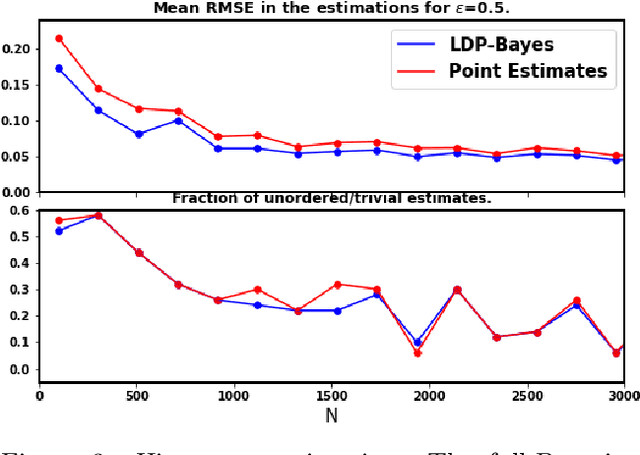
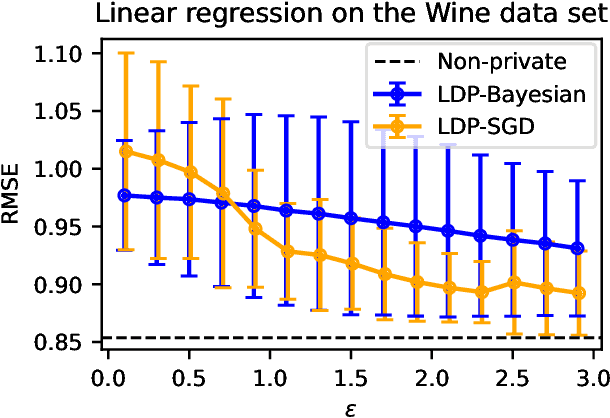
In recent years, local differential privacy (LDP) has emerged as a technique of choice for privacy-preserving data collection in several scenarios when the aggregator is not trustworthy. LDP provides client-side privacy by adding noise at the user's end. Thus, clients need not rely on the trustworthiness of the aggregator. In this work, we provide a noise-aware probabilistic modeling framework, which allows Bayesian inference to take into account the noise added for privacy under LDP, conditioned on locally perturbed observations. Stronger privacy protection (compared to the central model) provided by LDP protocols comes at a much harsher privacy-utility trade-off. Our framework tackles several computational and statistical challenges posed by LDP for accurate uncertainty quantification under Bayesian settings. We demonstrate the efficacy of our framework in parameter estimation for univariate and multi-variate distributions as well as logistic and linear regression.

Differentially Private Bayesian Inference for Generalized Linear Models

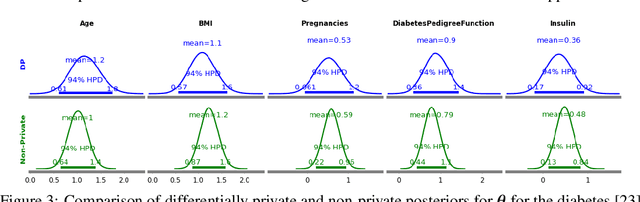
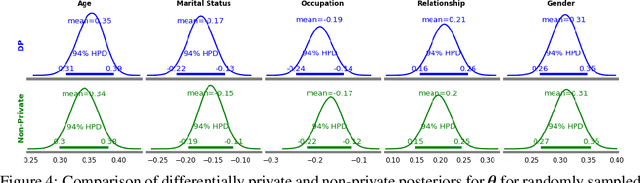
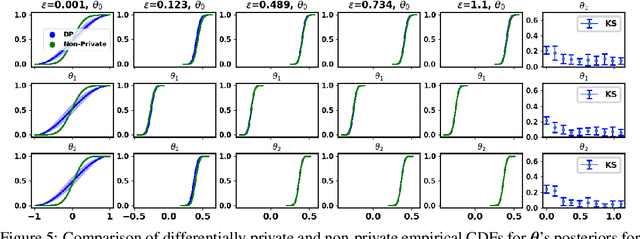
The framework of differential privacy (DP) upper bounds the information disclosure risk involved in using sensitive datasets for statistical analysis. A DP mechanism typically operates by adding carefully calibrated noise to the data release procedure. Generalized linear models (GLMs) are among the most widely used arms in data analyst's repertoire. In this work, with logistic and Poisson regression as running examples, we propose a generic noise-aware Bayesian framework to quantify the parameter uncertainty for a GLM at hand, given noisy sufficient statistics. We perform a tight privacy analysis and experimentally demonstrate that the posteriors obtained from our model, while adhering to strong privacy guarantees, are similar to the non-private posteriors.

Privacy-preserving Data Sharing on Vertically Partitioned Data

In this work, we present a method for differentially private data sharing by training a mixture model on vertically partitioned data, where each party holds different features for the same set of individuals. We use secure multi-party computation (MPC) to combine the contribution of the data from the parties to train the model. We apply the differentially private variational inference (DPVI) for learning the model. Assuming the mixture components contain no dependencies across different parties, the objective function can be factorized into a sum of products of individual components of each party. Therefore, each party can calculate its shares on its own without the use of MPC. Then MPC is only needed to get the product between the different shares and add the noise. Applying the method to demographic data from the US Census, we obtain comparable accuracy to the non-partitioned case with approximately 20-fold increase in computing time.