Jonathan Scarlett
Corruption-Tolerant Gaussian Process Bandit Optimization
Mar 04, 2020
Abstract:We consider the problem of optimizing an unknown (typically non-convex) function with a bounded norm in some Reproducing Kernel Hilbert Space (RKHS), based on noisy bandit feedback. We consider a novel variant of this problem in which the point evaluations are not only corrupted by random noise, but also adversarial corruptions. We introduce an algorithm Fast-Slow GP-UCB based on Gaussian process methods, randomized selection between two instances labeled "fast" (but non-robust) and "slow" (but robust), enlarged confidence bounds, and the principle of optimism under uncertainty. We present a novel theoretical analysis upper bounding the cumulative regret in terms of the corruption level, the time horizon, and the underlying kernel, and we argue that certain dependencies cannot be improved. We observe that distinct algorithmic ideas are required depending on whether one is required to perform well in both the corrupted and non-corrupted settings, and whether the corruption level is known or not.
Learning Gaussian Graphical Models via Multiplicative Weights
Feb 25, 2020Abstract:Graphical model selection in Markov random fields is a fundamental problem in statistics and machine learning. Two particularly prominent models, the Ising model and Gaussian model, have largely developed in parallel using different (though often related) techniques, and several practical algorithms with rigorous sample complexity bounds have been established for each. In this paper, we adapt a recently proposed algorithm of Klivans and Meka (FOCS, 2017), based on the method of multiplicative weight updates, from the Ising model to the Gaussian model, via non-trivial modifications to both the algorithm and its analysis. The algorithm enjoys a sample complexity bound that is qualitatively similar to others in the literature, has a low runtime $O(mp^2)$ in the case of $m$ samples and $p$ nodes, and can trivially be implemented in an online manner.
Sample Complexity Bounds for 1-bit Compressive Sensing and Binary Stable Embeddings with Generative Priors
Feb 12, 2020
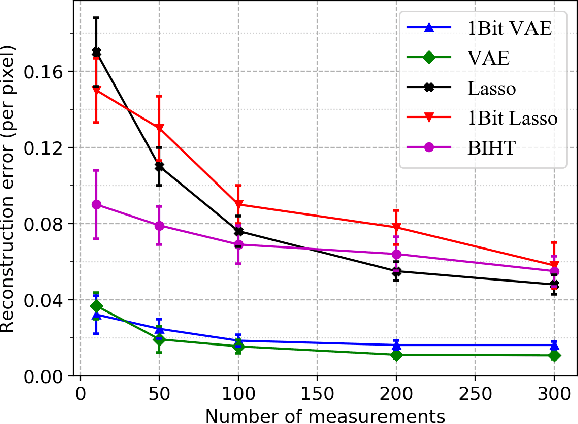
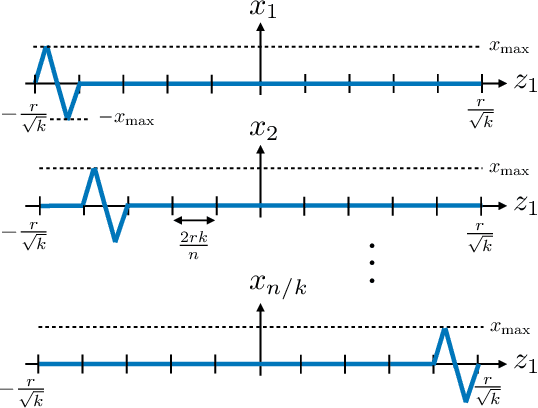
Abstract:The goal of standard 1-bit compressive sensing is to accurately recover an unknown sparse vector from binary-valued measurements, each indicating the sign of a linear function of the vector. Motivated by recent advances in compressive sensing with generative models, where a generative modeling assumption replaces the usual sparsity assumption, we study the problem of 1-bit compressive sensing with generative models. We first consider noiseless 1-bit measurements, and provide sample complexity bounds for approximate recovery under i.i.d.~Gaussian measurements and a Lipschitz continuous generative prior, as well as a near-matching algorithm-independent lower bound. Moreover, we demonstrate that the Binary $\epsilon$-Stable Embedding property, which characterizes the robustness of the reconstruction to measurement errors and noise, also holds for 1-bit compressive sensing with Lipschitz continuous generative models with sufficiently many Gaussian measurements. In addition, we apply our results to neural network generative models, and provide a proof-of-concept numerical experiment demonstrating significant improvements over sparsity-based approaches.
Tight Regret Bounds for Noisy Optimization of a Brownian Motion
Jan 25, 2020
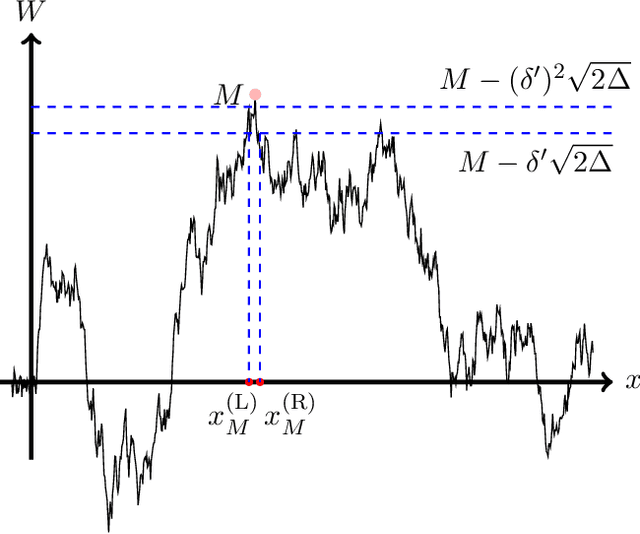
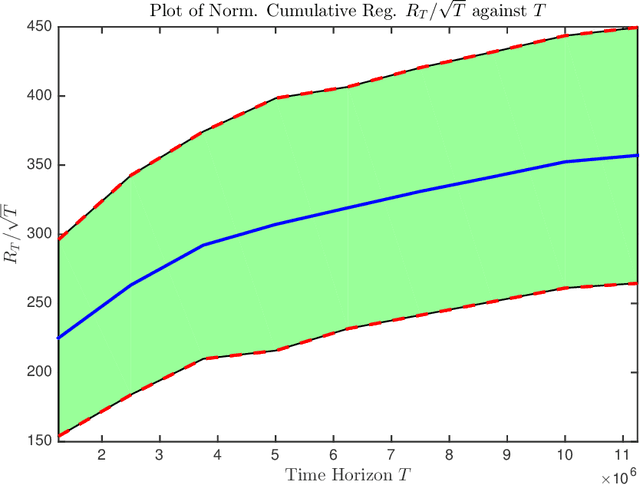
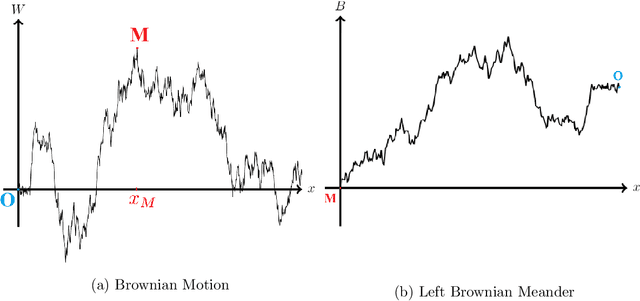
Abstract:We consider the problem of Bayesian optimization of a one-dimensional Brownian motion in which the $T$ adaptively chosen observations are corrupted by Gaussian noise. We show that as the smallest possible expected simple regret and the smallest possible expected cumulative regret scale as $\Omega(1 / \sqrt{T \log (T)}) \cap \mathcal{O}(\log T / \sqrt{T})$ and $\Omega(\sqrt{T / \log (T)}) \cap \mathcal{O}(\sqrt{T} \cdot \log T)$ respectively. Thus, our upper and lower bounds are tight up to a factor of $\mathcal{O}( (\log T)^{1.5} )$. The upper bound uses an algorithm based on confidence bounds and the Markov property of Brownian motion, and the lower bound is based on a reduction to binary hypothesis testing.
A Characteristic Function Approach to Deep Implicit Generative Modeling
Sep 16, 2019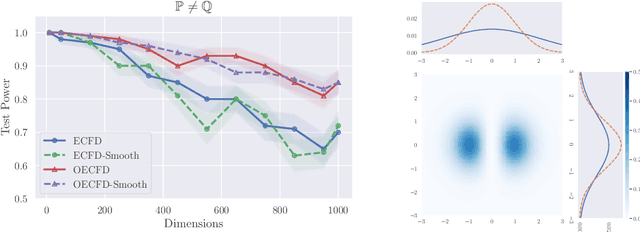
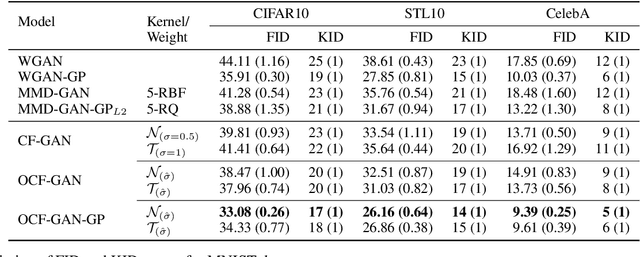
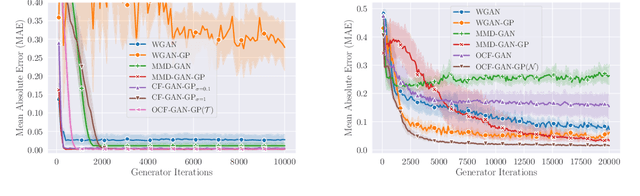
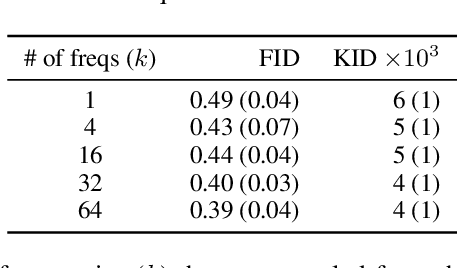
Abstract:In this paper, we formulate the problem of learning an Implicit Generative Model (IGM) as minimizing the expected distance between characteristic functions. Specifically, we match the characteristic functions of the real and generated data distributions under a suitably-chosen weighting distribution. This distance measure, which we term as the characteristic function distance (CFD), can be (approximately) computed with linear time-complexity in the number of samples, compared to the quadratic-time Maximum Mean Discrepancy (MMD). By replacing the discrepancy measure in the critic of a GAN with the CFD, we obtain a model that is simple to implement and stable to train; the proposed metric enjoys desirable theoretical properties including continuity and differentiability with respect to generator parameters, and continuity in the weak topology. We further propose a variation of the CFD in which the weighting distribution parameters are also optimized during training; this obviates the need for manual tuning and leads to an improvement in test power relative to CFD. Experiments show that our proposed method outperforms WGAN and MMD-GAN variants on a variety of unsupervised image generation benchmark datasets.
Information-Theoretic Lower Bounds for Compressive Sensing with Generative Models
Aug 28, 2019
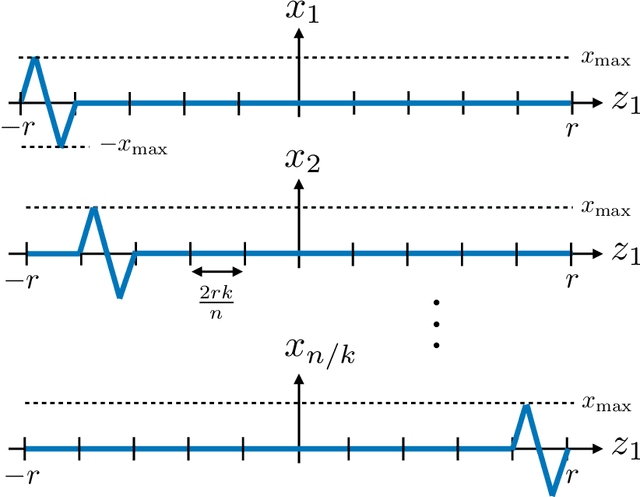
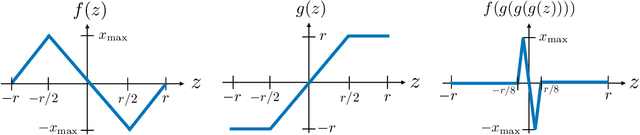
Abstract:The goal of standard compressive sensing is to estimate an unknown vector from linear measurements under the assumption of sparsity in some basis. Recently, it has been shown that significantly fewer measurements may be required if the sparsity assumption is replaced by the assumption that the unknown vector lies near the range of a suitably-chosen generative model. In particular, in (Bora {\em et al.}, 2017) it was shown that roughly $O(k\log L)$ random Gaussian measurements suffice for accurate recovery when the $k$-input generative model is bounded and $L$-Lipschitz, and that $O(kd \log w)$ measurements suffice for $k$-input ReLU networks with depth $d$ and width $w$. In this paper, we establish corresponding algorithm-independent lower bounds on the sample complexity using tools from minimax statistical analysis. In accordance with the above upper bounds, our results are summarized as follows: (i) We construct an $L$-Lipschitz generative model capable of generating group-sparse signals, and show that the resulting necessary number of measurements is $\Omega(k \log L)$; (ii) Using similar ideas, we construct two-layer ReLU networks of high width requiring $\Omega(k \log w)$ measurements, as well as lower-width deep ReLU networks requiring $\Omega(k d)$ measurements. As a result, we establish that the scaling laws derived in (Bora {\em et al.}, 2017) are optimal or near-optimal in the absence of further assumptions.
Learning Erdős-Rényi Random Graphs via Edge Detecting Queries
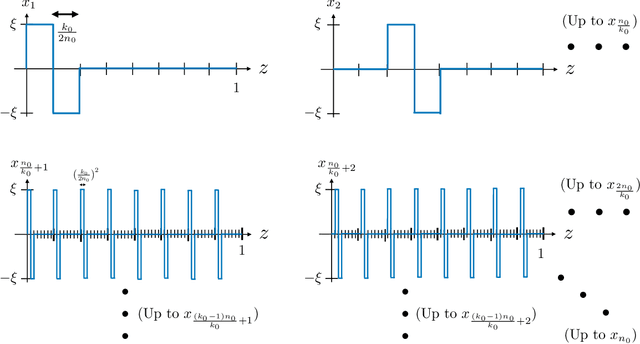
May 11, 2019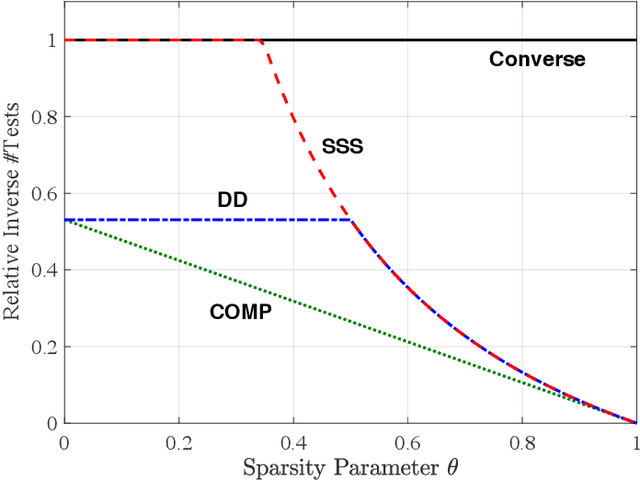
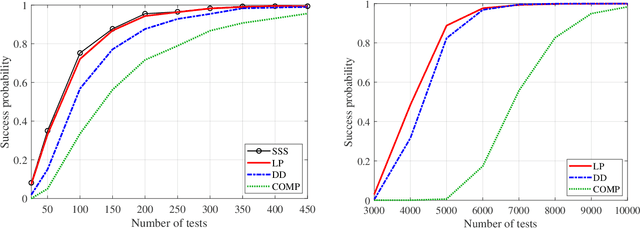
Abstract:In this paper, we consider the problem of learning an unknown graph via queries on groups of nodes, with the result indicating whether or not at least one edge is present among those nodes. While learning arbitrary graphs with $n$ nodes and $k$ edges is known to be hard the sense of requiring $\Omega( \min\{ k^2 \log n, n^2\})$ tests (even when a small probability of error is allowed), we show that learning an Erd\H{o}s-R\'enyi random graph with an average of $\bar{k}$ edges is much easier; namely, one can attain asymptotically vanishing error probability with only $O(\bar{k} \log n)$ tests. We establish such bounds for a variety of algorithms inspired by the group testing problem, with explicit constant factors indicating a near-optimal number of tests, and in some cases asymptotic optimality including constant factors. In addition, we present an alternative design that permits a near-optimal sublinear decoding time of $O(\bar{k} \log^2 \bar{k} + \bar{k} \log n)$.
Support Recovery in the Phase Retrieval Model: Information-Theoretic Fundamental Limits
Jan 30, 2019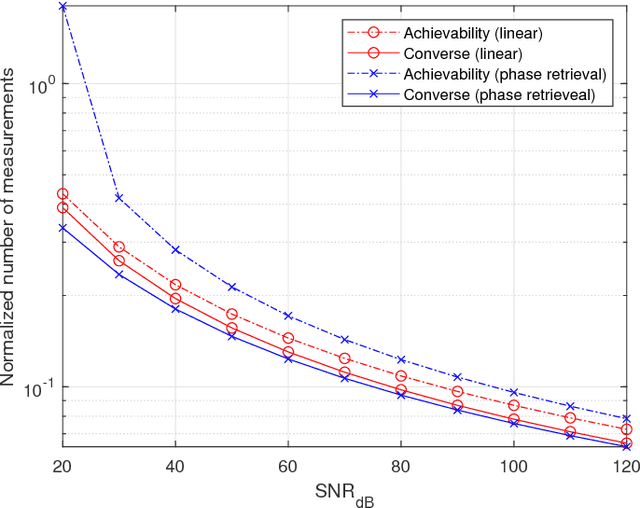
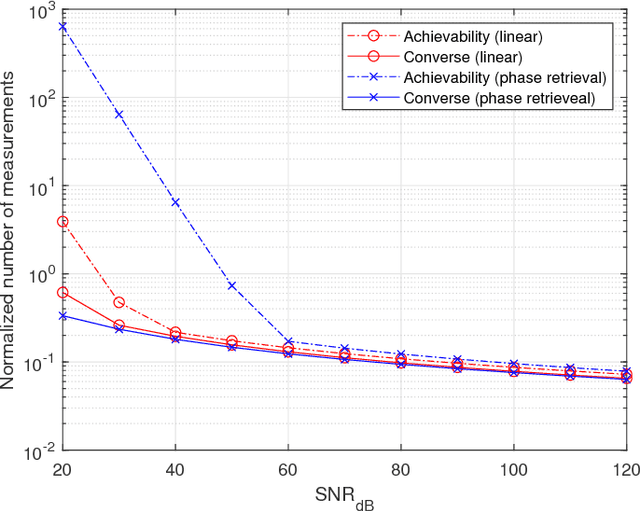
Abstract:The support recovery problem consists of determining a sparse subset of variables that is relevant in generating a set of observations. In this paper, we study the support recovery problem in the phase retrieval model consisting of noisy phaseless measurements, which arises in a diverse range of settings such as optical detection, X-ray crystallography, electron microscopy, and coherent diffractive imaging. Our focus is on information-theoretic fundamental limits under an approximate recovery criterion, considering both discrete and Gaussian models for the sparse non-zero entries. In both cases, our bounds provide sharp thresholds with near-matching constant factors in several scaling regimes on the sparsity and signal-to-noise ratio. As a key step towards obtaining these results, we develop new concentration bounds for the conditional information content of log-concave random variables, which may be of independent interest.
An Introductory Guide to Fano's Inequality with Applications in Statistical Estimation
Jan 02, 2019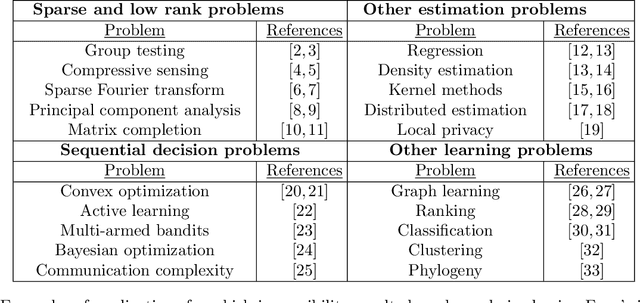
Abstract:Information theory plays an indispensable role in the development of algorithm-independent impossibility results, both for communication problems and for seemingly distinct areas such as statistics and machine learning. While numerous information-theoretic tools have been proposed for this purpose, the oldest one remains arguably the most versatile and widespread: Fano's inequality. In this chapter, we provide a survey of Fano's inequality and its variants in the context of statistical estimation, adopting a versatile framework that covers a wide range of specific problems. We present a variety of key tools and techniques used for establishing impossibility results via this approach, and provide representative examples covering group testing, graphical model selection, sparse linear regression, density estimation, and convex optimization.
Adversarially Robust Optimization with Gaussian Processes
Nov 01, 2018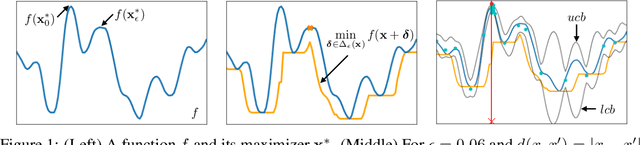
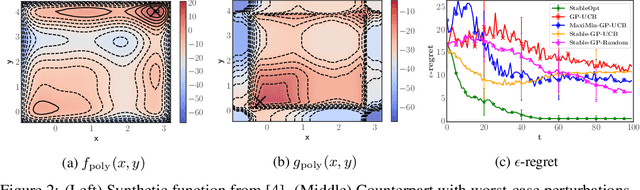
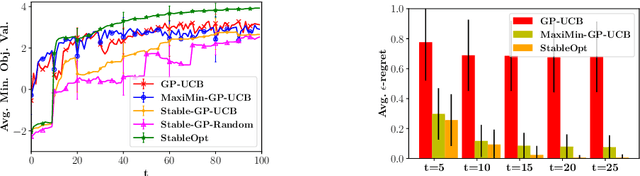
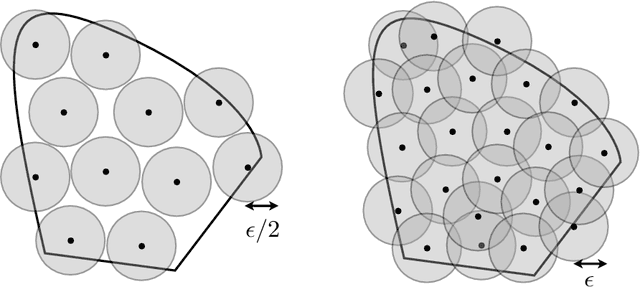
Abstract:In this paper, we consider the problem of Gaussian process (GP) optimization with an added robustness requirement: The returned point may be perturbed by an adversary, and we require the function value to remain as high as possible even after this perturbation. This problem is motivated by settings in which the underlying functions during optimization and implementation stages are different, or when one is interested in finding an entire region of good inputs rather than only a single point. We show that standard GP optimization algorithms do not exhibit the desired robustness properties, and provide a novel confidence-bound based algorithm StableOpt for this purpose. We rigorously establish the required number of samples for StableOpt to find a near-optimal point, and we complement this guarantee with an algorithm-independent lower bound. We experimentally demonstrate several potential applications of interest using real-world data sets, and we show that StableOpt consistently succeeds in finding a stable maximizer where several baseline methods fail.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge