Convex Maneuver Planning for Spacecraft Collision Avoidance

Conjunction analysis and maneuver planning for spacecraft collision avoidance remains a manual and time-consuming process, typically involving repeated forward simulations of hand-designed maneuvers. With the growing density of satellites in low-Earth orbit (LEO), autonomy is becoming essential for efficiently evaluating and mitigating collisions. In this work, we present an algorithm to design low-thrust collision-avoidance maneuvers for short-term conjunction events. We first formulate the problem as a nonconvex quadratically-constrained quadratic program (QCQP), which we then relax into a convex semidefinite program (SDP) using Shor's relaxation. We demonstrate empirically that the relaxation is tight, which enables the recovery of globally optimal solutions to the original nonconvex problem. Our formulation produces a minimum-energy solution while ensuring a desired probability of collision at the time of closest approach. Finally, if the desired probability of collision cannot be satisfied, we relax this constraint into a penalty, yielding a minimum-risk solution. We validate our algorithm with a high-fidelity simulation of a satellite conjunction in low-Earth orbit with a simulated conjunction data message (CDM), demonstrating its effectiveness in reducing collision risk.

The Trajectory Bundle Method: Unifying Sequential-Convex Programming and Sampling-Based Trajectory Optimization

We present a unified framework for solving trajectory optimization problems in a derivative-free manner through the use of sequential convex programming. Traditionally, nonconvex optimization problems are solved by forming and solving a sequence of convex optimization problems, where the cost and constraint functions are approximated locally through Taylor series expansions. This presents a challenge for functions where differentiation is expensive or unavailable. In this work, we present a derivative-free approach to form these convex approximations by computing samples of the dynamics, cost, and constraint functions and letting the solver interpolate between them. Our framework includes sample-based trajectory optimization techniques like model-predictive path integral (MPPI) control as a special case and generalizes them to enable features like multiple shooting and general equality and inequality constraints that are traditionally associated with derivative-based sequential convex programming methods. The resulting framework is simple, flexible, and capable of solving a wide variety of practical motion planning and control problems.

PHODCOS: Pythagorean Hodograph-based Differentiable Coordinate System

This paper presents PHODCOS, an algorithm that assigns a moving coordinate system to a given curve. The parametric functions underlying the coordinate system, i.e., the path function, the moving frame and its angular velocity, are exact -- approximation free -- differentiable, and sufficiently continuous. This allows for computing a coordinate system for highly nonlinear curves, while remaining compliant with autonomous navigation algorithms that require first and second order gradient information. In addition, the coordinate system obtained by PHODCOS is fully defined by a finite number of coefficients, which may then be used to compute additional geometric properties of the curve, such as arc-length, curvature, torsion, etc. Therefore, PHODCOS presents an appealing paradigm to enhance the geometrical awareness of existing guidance and navigation on-orbit spacecraft maneuvers. The PHODCOS algorithm is presented alongside an analysis of its error and approximation order, and thus, it is guaranteed that the obtained coordinate system matches the given curve within a desired tolerance. To demonstrate the applicability of the coordinate system resulting from PHODCOS, we present numerical examples in the Near Rectilinear Halo Orbit (NRHO) for the Lunar Gateway.

A Universal Formulation for Path-Parametric Planning and Control

This work presents a unified framework for path-parametric planning and control. This formulation is universal as it standardizes the entire spectrum of path-parametric techniques -- from traditional path following to more recent contouring or progress-maximizing Model Predictive Control and Reinforcement Learning -- under a single framework. The ingredients underlying this universality are twofold: First, we present a compact and efficient technique capable of computing singularity-free, smooth and differentiable moving frames. Second, we derive a spatial path parameterization of the Cartesian coordinates applicable to any arbitrary curve without prior assumptions on its parametric speed or moving frame, and that perfectly interplays with the aforementioned path parameterization method. The combination of these two ingredients leads to a planning and control framework that brings togehter existing path-parametric techniques in literature. Aiming to unify all these approaches, we open source PACOR, a software library that implements the presented content, thereby providing a self-contained toolkit for the formulation of path-parametric planning and control methods.

Differentiable Collision-Free Parametric Corridors

This paper presents a method to compute differentiable collision-free parametric corridors. In contrast to existing solutions that decompose the obstacle-free space into multiple convex sets, the continuous corridors computed by our method are smooth and differentiable, making them compatible with existing numerical techniques for learning and optimization. To achieve this, we represent the collision-free corridors as a path-parametric off-centered ellipse with a polynomial basis. We show that the problem of maximizing the volume of such corridors is convex, and can be efficiently solved. To assess the effectiveness of the proposed method, we examine its performance in a synthetic case study and subsequently evaluate its applicability in a real-world scenario from the KITTI dataset.

Geometric Slosh-Free Tracking for Robotic Manipulators

This work focuses on the agile transportation of liquids with robotic manipulators. In contrast to existing methods that are either computationally heavy, system/container specific or dependant on a singularity-prone pendulum model, we present a real-time slosh-free tracking technique. This method solely requires the reference trajectory and the robot's kinematic constraints to output kinematically feasible joint space commands. The crucial element underlying this approach consists on mimicking the end-effector's motion through a virtual quadrotor, which is inherently slosh-free and differentially flat, thereby allowing us to calculate a slosh-free reference orientation. Through the utilization of a cascaded proportional-derivative (PD) controller, this slosh-free reference is transformed into task space acceleration commands, which, following the resolution of a Quadratic Program (QP) based on Resolved Acceleration Control (RAC), are translated into a feasible joint configuration. The validity of the proposed approach is demonstrated by simulated and real-world experiments on a 7 DoF Franka Emika Panda robot. Code: https://github.com/jonarriza96/gsft Video: https://youtu.be/4kitqYVS9n8

Learning for CasADi: Data-driven Models in Numerical Optimization

While real-world problems are often challenging to analyze analytically, deep learning excels in modeling complex processes from data. Existing optimization frameworks like CasADi facilitate seamless usage of solvers but face challenges when integrating learned process models into numerical optimizations. To address this gap, we present the Learning for CasADi (L4CasADi) framework, enabling the seamless integration of PyTorch-learned models with CasADi for efficient and potentially hardware-accelerated numerical optimization. The applicability of L4CasADi is demonstrated with two tutorial examples: First, we optimize a fish's trajectory in a turbulent river for energy efficiency where the turbulent flow is represented by a PyTorch model. Second, we demonstrate how an implicit Neural Radiance Field environment representation can be easily leveraged for optimal control with L4CasADi. L4CasADi, along with examples and documentation, is available under MIT license at https://github.com/Tim-Salzmann/l4casadi

Pose-Following with Dual Quaternions

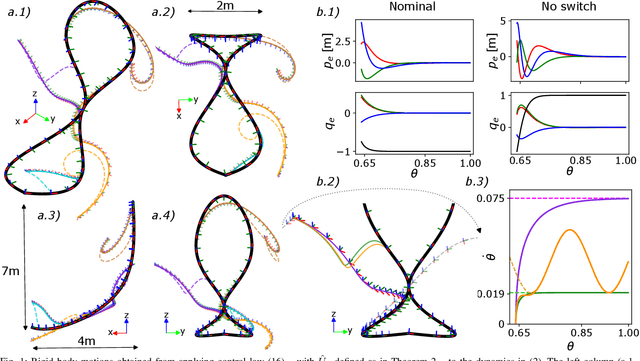
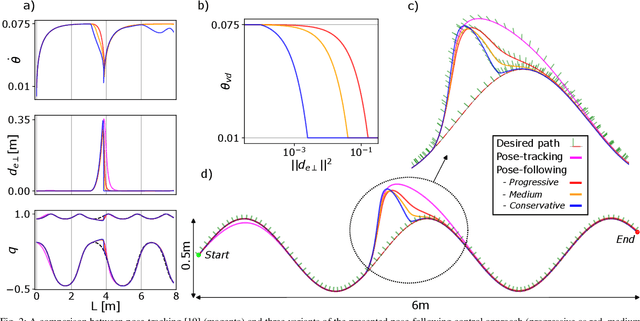
This work focuses on pose-following, a variant of path-following in which the goal is to steer the system's position and attitude along a path with a moving frame attached to it. Full body motion control, while accounting for the additional freedom to self-regulate the progress along the path, is an appealing trade-off. Towards this end, we extend the well-established dual quaternion-based pose-tracking method into a pose-following control law. Specifically, we derive the equations of motion for the full pose error between the geometric reference and the rigid body in the form of a dual quaternion and dual twist. Subsequently, we formulate an almost globally asymptotically stable control law. The global attractivity of the presented approach is validated in a spatial example, while its benefits over pose-tracking are showcased through a planar case-study.

Spatially Constrained Time-Optimal Motion Planning

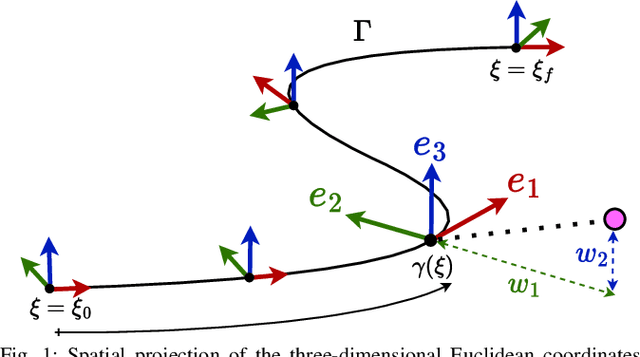
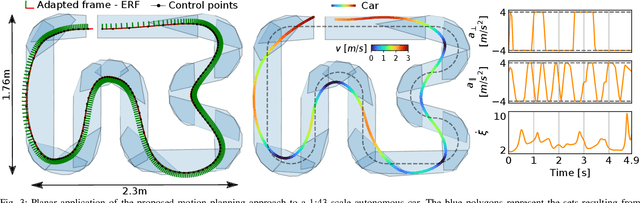
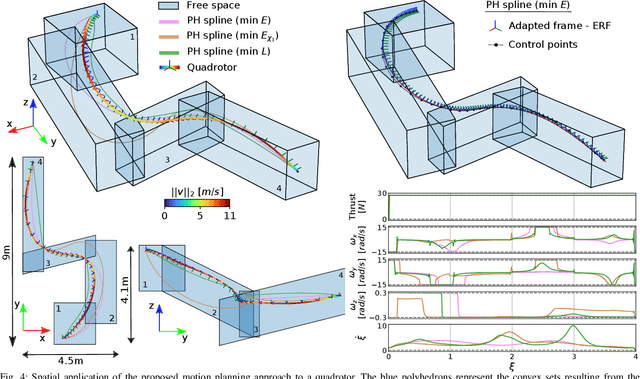
This paper focuses on spatial time-optimal motion planning, a generalization of the exact time-optimal path following problem that allows the system to plan within a predefined space. In contrast to state-of-the-art methods, we drop the assumption that a collision-free geometric reference is given. Instead, we present a two-stage motion planning method that solely relies on a goal location and a geometric representation of the environment to compute a time-optimal trajectory that is compliant with system dynamics and constraints. To do so, the proposed scheme first computes an obstacle-free Pythagorean Hodograph parametric spline, and second solves a spatially reformulated minimum-time optimization problem. The spline obtained in the first stage is not a geometric reference, but an extension of the environment representation, and thus, time-optimality of the solution is guaranteed. The efficacy of the proposed approach is benchmarked by a known planar example and validated in a more complex spatial system, illustrating its versatility and applicability.

Spatial motion planning with Pythagorean Hodograph curves

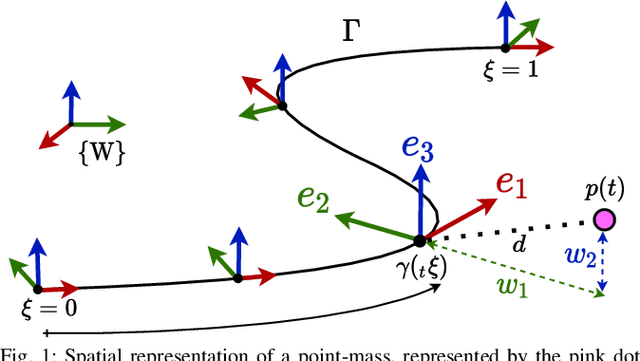
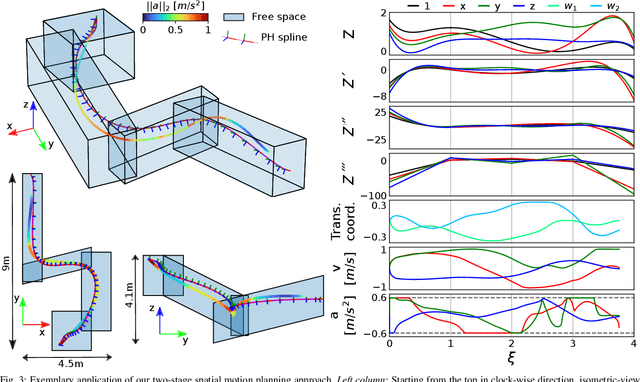
This paper presents a two-stage prediction-based control scheme for embedding the environment's geometric properties into a collision-free Pythagorean Hodograph spline, and subsequently finding the optimal path within the parameterized free space. The ingredients of this approach are twofold: First, we present a novel spatial path parameterization applicable to any arbitrary curve without prior assumptions in its adapted frame. Second, we identify the appropriateness of Pythagorean Hodograph curves for a compact and continuous definition of the path-parametric functions required by the presented spatial model. This dual-stage formulation results in a motion planning approach, where the geometric properties of the environment arise as states of the prediction model. Thus, the presented method is attractive for motion planning in dense environments. The efficacy of the approach is evaluated according to an illustrative example.