Graph Matching with Partially-Correct Seeds

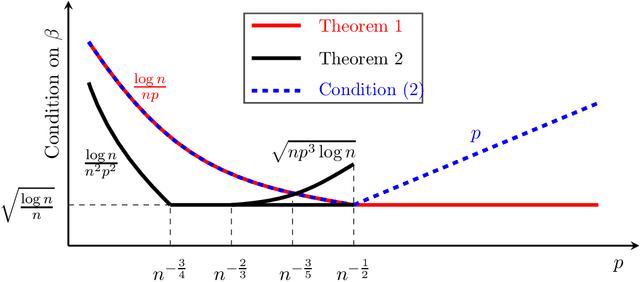
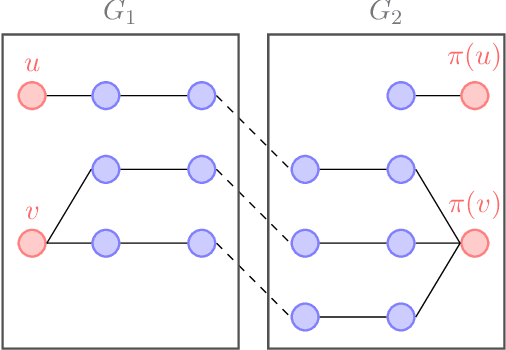
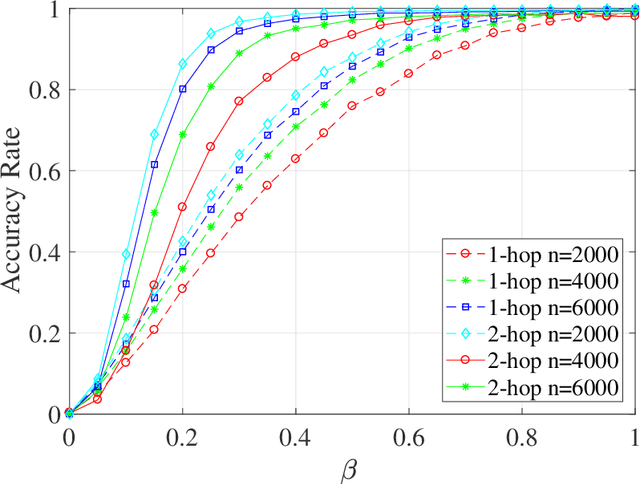
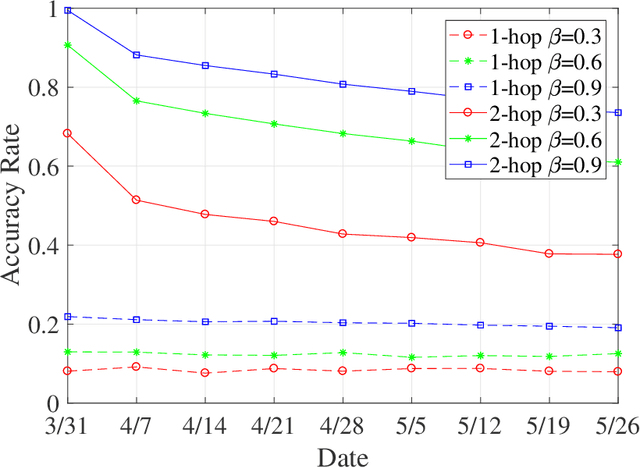
The graph matching problem aims to find the latent vertex correspondence between two edge-correlated graphs and has many practical applications. In this work, we study a version of the seeded graph matching problem, which assumes that a set of seeds, i.e., pre-mapped vertex-pairs, is given in advance. Specifically, consider two correlated graphs whose edges are sampled independently with probability $s$ from a parent \ER graph $\mathcal{G}(n,p)$. Furthermore, a mapping between the vertices of the two graphs is provided as seeds, of which an unknown $\beta$ fraction is correct. This problem was first studied in \cite{lubars2018correcting} where an algorithm is proposed and shown to perfectly recover the correct vertex mapping with high probability if $\beta\geq\max\left\{\frac{8}{3}p,\frac{16\log{n}}{nps^2}\right\}$. We improve their condition to $\beta\geq\max\left\{30\sqrt{\frac{\log n}{n(1-p)^2s^2}},\frac{45\log{n}}{np(1-p)^2s^2}\right)$. However, when $p=O\left( \sqrt{{\log n}/{ns^2}}\right)$, our improved condition still requires that $\beta$ must increase inversely proportional to $np$. In order to improve the matching performance for sparse graphs, we propose a new algorithm that uses "witnesses" in the 2-hop neighborhood, instead of only 1-hop neighborhood as in \cite{lubars2018correcting}. We show that when $np^2\leq\frac{1}{135\log n}$, our new algorithm can achieve perfect recovery with high probability if $\beta\geq\max\left\{900\sqrt{\frac{np^3(1-s)\log n}{s}},600\sqrt{\frac{\log n}{ns^4}}, \frac{1200\log n}{n^2p^2s^4}\right\}$ and $nps^2\geq 128\log n$. Numerical experiments on both synthetic and real graphs corroborate our theoretical findings and show that our 2-hop algorithm significantly outperforms the 1-hop algorithm when the graphs are relatively sparse.

The Planted Matching Problem: Phase Transitions and Exact Results

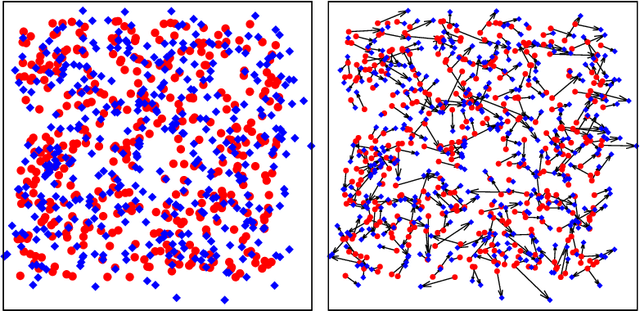
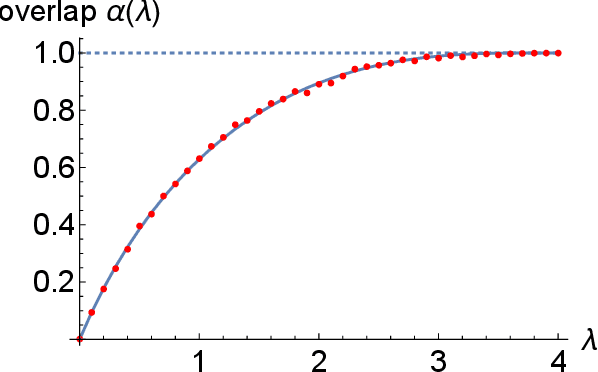
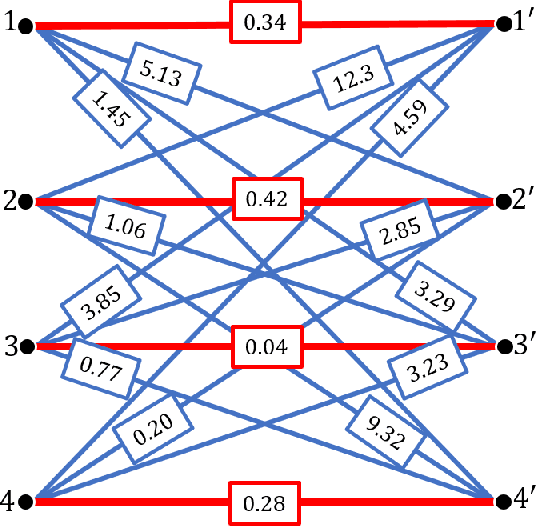
We study the problem of recovering a planted matching in randomly weighted complete bipartite graphs $K_{n,n}$. For some unknown perfect matching $M^*$, the weight of an edge is drawn from one distribution $P$ if $e \in M^*$ and another distribution $Q$ if $e \in M^*$. Our goal is to infer $M^*$, exactly or approximately, from the edge weights. In this paper we take $P=\exp(\lambda)$ and $Q=\exp(1/n)$, in which case the maximum-likelihood estimator of $M^*$ is the minimum-weight matching $M_{\min}$. We obtain precise results on the overlap between $M^*$ and $M_{\min}$, i.e., the fraction of edges they have in common. For $\lambda \ge 4$ we have almost-perfect recovery, with overlap $1-o(1)$ with high probability. For $\lambda < 4$ the expected overlap is an explicit function $\alpha(\lambda) < 1$: we compute it by generalizing Aldous' celebrated proof of M\'ezard and Parisi's $\zeta(2)$ conjecture for the un-planted model, using local weak convergence to relate $K_{n,n}$ to a type of weighted infinite tree, and then deriving a system of differential equations from a message-passing algorithm on this tree.

DMRM: A Dual-channel Multi-hop Reasoning Model for Visual Dialog

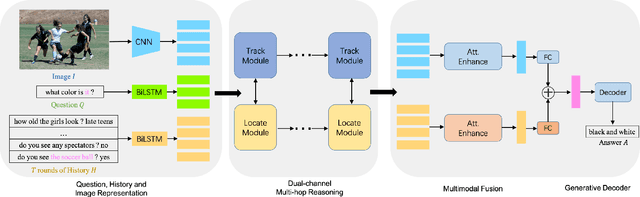
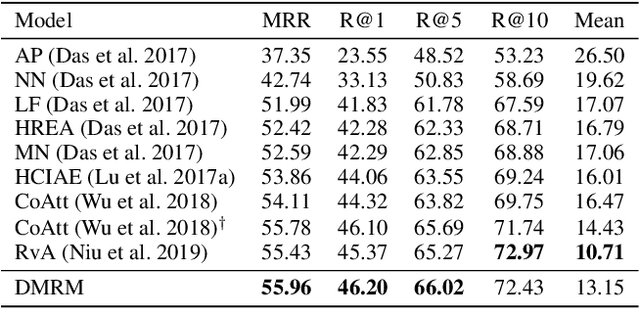
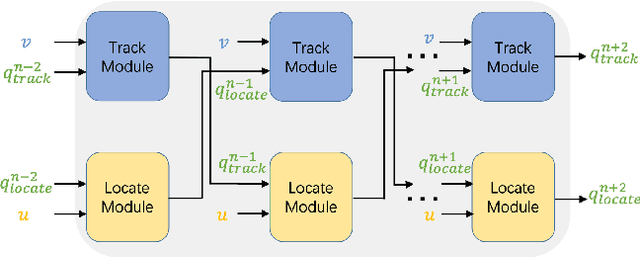
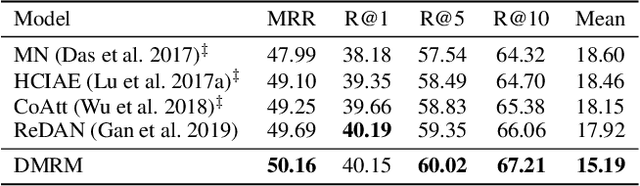
Visual Dialog is a vision-language task that requires an AI agent to engage in a conversation with humans grounded in an image. It remains a challenging task since it requires the agent to fully understand a given question before making an appropriate response not only from the textual dialog history, but also from the visually-grounded information. While previous models typically leverage single-hop reasoning or single-channel reasoning to deal with this complex multimodal reasoning task, which is intuitively insufficient. In this paper, we thus propose a novel and more powerful Dual-channel Multi-hop Reasoning Model for Visual Dialog, named DMRM. DMRM synchronously captures information from the dialog history and the image to enrich the semantic representation of the question by exploiting dual-channel reasoning. Specifically, DMRM maintains a dual channel to obtain the question- and history-aware image features and the question- and image-aware dialog history features by a mulit-hop reasoning process in each channel. Additionally, we also design an effective multimodal attention to further enhance the decoder to generate more accurate responses. Experimental results on the VisDial v0.9 and v1.0 datasets demonstrate that the proposed model is effective and outperforms compared models by a significant margin.

Consistent recovery threshold of hidden nearest neighbor graphs

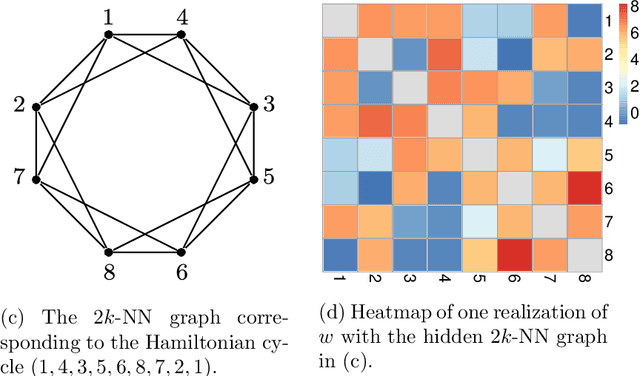
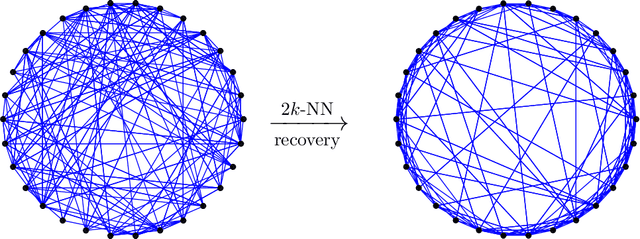
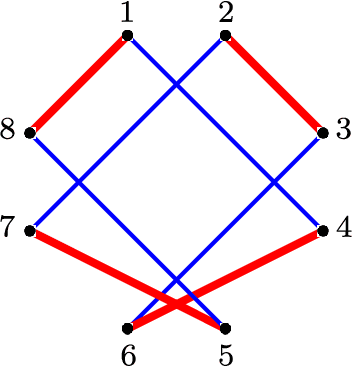
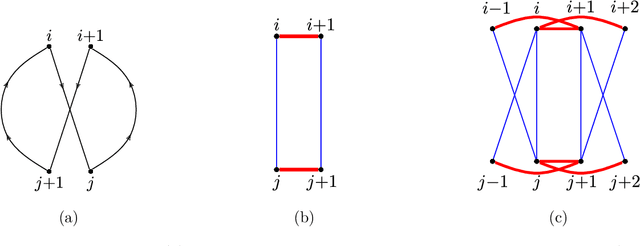
Motivated by applications such as discovering strong ties in social networks and assembling genome subsequences in biology, we study the problem of recovering a hidden $2k$-nearest neighbor (NN) graph in an $n$-vertex complete graph, whose edge weights are independent and distributed according to $P_n$ for edges in the hidden $2k$-NN graph and $Q_n$ otherwise. The special case of Bernoulli distributions corresponds to a variant of the Watts-Strogatz small-world graph. We focus on two types of asymptotic recovery guarantees as $n\to \infty$: (1) exact recovery: all edges are classified correctly with probability tending to one; (2) almost exact recovery: the expected number of misclassified edges is $o(nk)$. We show that the maximum likelihood estimator achieves (1) exact recovery for $2 \le k \le n^{o(1)}$ if $ \liminf \frac{2\alpha_n}{\log n}>1$; (2) almost exact recovery for $ 1 \le k \le o\left( \frac{\log n}{\log \log n} \right)$ if $\liminf \frac{kD(P_n||Q_n)}{\log n}>1$, where $\alpha_n \triangleq -2 \log \int \sqrt{d P_n d Q_n}$ is the R\'enyi divergence of order $\frac{1}{2}$ and $D(P_n||Q_n)$ is the Kullback-Leibler divergence. Under mild distributional assumptions, these conditions are shown to be information-theoretically necessary for any algorithm to succeed. A key challenge in the analysis is the enumeration of $2k$-NN graphs that differ from the hidden one by a given number of edges.

Optimal query complexity for private sequential learning

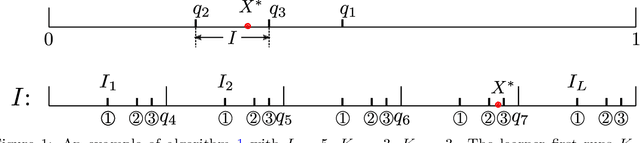
Motivated by privacy concerns in many practical applications such as Federated Learning, we study a stylized private sequential learning problem: a learner tries to estimate an unknown scalar value, by sequentially querying an external database and receiving binary responses; meanwhile, a third-party adversary observes the learner's queries but not the responses. The learner's goal is to design a querying strategy with the minimum number of queries (optimal query complexity) so that she can accurately estimate the true value, while the adversary even with the complete knowledge of her querying strategy cannot. Prior work has obtained both upper and lower bounds on the optimal query complexity, however, these upper and lower bounds have a large gap in general. In this paper, we construct new querying strategies and prove almost matching upper and lower bounds, providing a complete characterization of the optimal query complexity as a function of the estimation accuracy and the desired levels of privacy.

Spectral Graph Matching and Regularized Quadratic Relaxations II: Erdős-Rényi Graphs and Universality

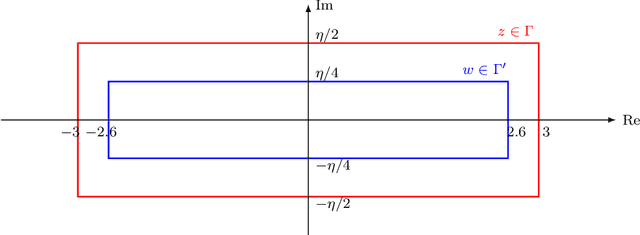
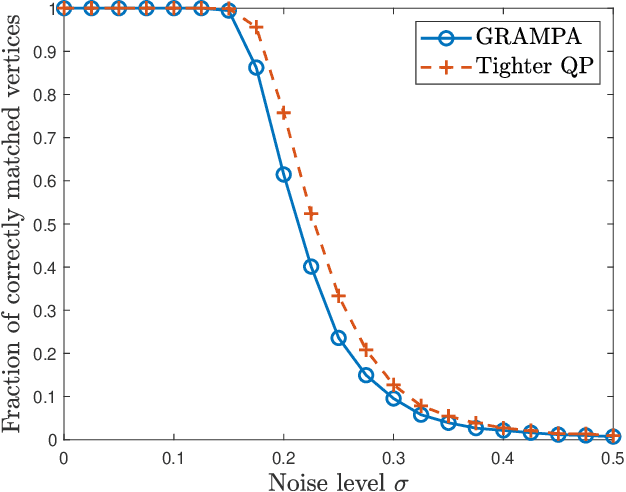
We analyze a new spectral graph matching algorithm, GRAph Matching by Pairwise eigen-Alignments (GRAMPA), for recovering the latent vertex correspondence between two unlabeled, edge-correlated weighted graphs. Extending the exact recovery guarantees established in the companion paper for Gaussian weights, in this work, we prove the universality of these guarantees for a general correlated Wigner model. In particular, for two Erd\H{o}s-R\'enyi graphs with edge correlation coefficient $1-\sigma^2$ and average degree at least $\operatorname{polylog}(n)$, we show that GRAMPA exactly recovers the latent vertex correspondence with high probability when $\sigma \lesssim 1/\operatorname{polylog}(n)$. Moreover, we establish a similar guarantee for a variant of GRAMPA, corresponding to a tighter quadratic programming relaxation of the quadratic assignment problem. Our analysis exploits a resolvent representation of the GRAMPA similarity matrix and local laws for the resolvents of sparse Wigner matrices.

Spectral Graph Matching and Regularized Quadratic Relaxations I: The Gaussian Model

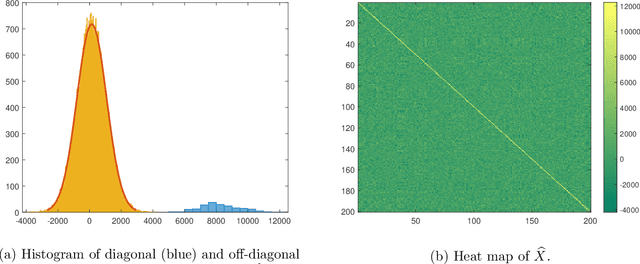
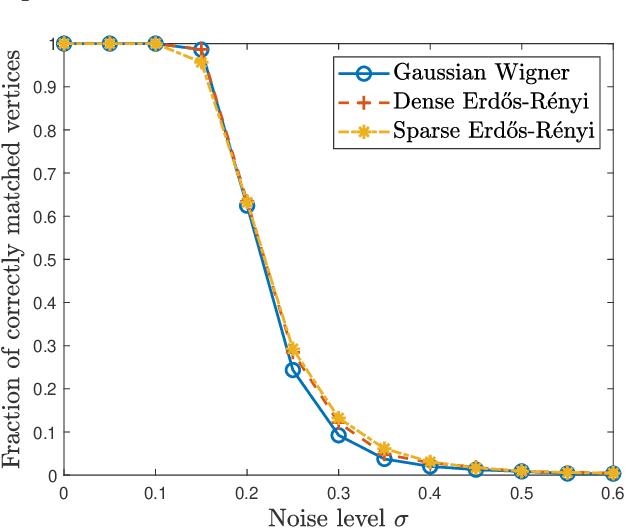
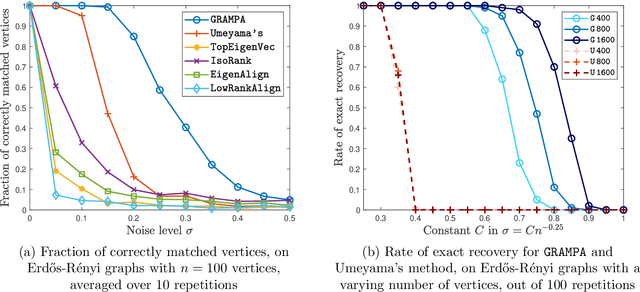
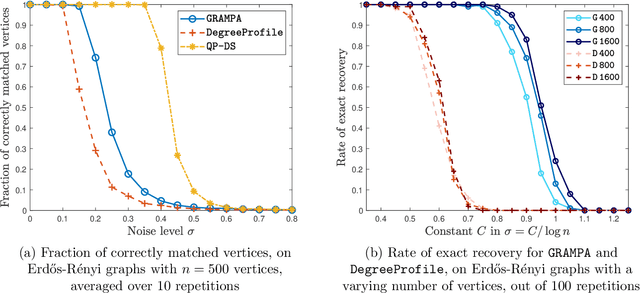
Graph matching aims at finding the vertex correspondence between two unlabeled graphs that maximizes the total edge weight correlation. This amounts to solving a computationally intractable quadratic assignment problem. In this paper we propose a new spectral method, GRAph Matching by Pairwise eigen-Alignments (GRAMPA). Departing from prior spectral approaches that only compare top eigenvectors, or eigenvectors of the same order, GRAMPA first constructs a similarity matrix as a weighted sum of outer products between all pairs of eigenvectors of the two graphs, with weights given by a Cauchy kernel applied to the separation of the corresponding eigenvalues, then outputs a matching by a simple rounding procedure. The similarity matrix can also be interpreted as the solution to a regularized quadratic programming relaxation of the quadratic assignment problem. For the Gaussian Wigner model in which two complete graphs on $n$ vertices have Gaussian edge weights with correlation coefficient $1-\sigma^2$, we show that GRAMPA exactly recovers the correct vertex correspondence with high probability when $\sigma = O(\frac{1}{\log n})$. This matches the state of the art of polynomial-time algorithms, and significantly improves over existing spectral methods which require $\sigma$ to be polynomially small in $n$. The superiority of GRAMPA is also demonstrated on a variety of synthetic and real datasets, in terms of both statistical accuracy and computational efficiency. Universality results, including similar guarantees for dense and sparse Erd\H{o}s-R\'{e}nyi graphs, are deferred to the companion paper.

Efficient random graph matching via degree profiles

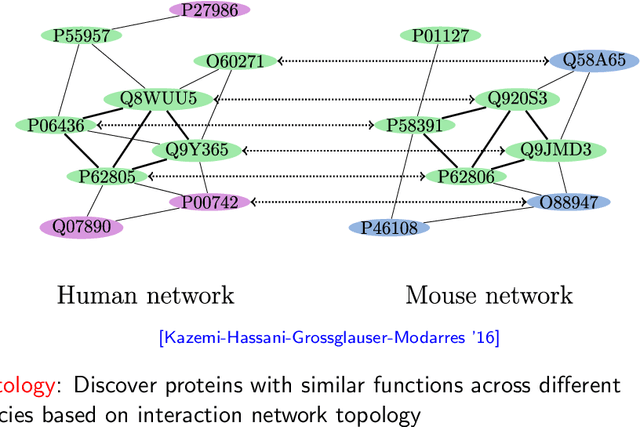
Random graph matching refers to recovering the underlying vertex correspondence between two random graphs with correlated edges; a prominent example is when the two random graphs are given by Erd\H{o}s-R\'{e}nyi graphs $G(n,\frac{d}{n})$. This can be viewed as an average-case and noisy version of the graph isomorphism problem. Under this model, the maximum likelihood estimator is equivalent to solving the intractable quadratic assignment problem. This work develops an $\tilde{O}(n d^2+n^2)$-time algorithm which perfectly recovers the true vertex correspondence with high probability, provided that the average degree is at least $d = \Omega(\log^2 n)$ and the two graphs differ by at most $\delta = O( \log^{-2}(n) )$ fraction of edges. For dense graphs and sparse graphs, this can be improved to $\delta = O( \log^{-2/3}(n) )$ and $\delta = O( \log^{-2}(d) )$ respectively, both in polynomial time. The methodology is based on appropriately chosen distance statistics of the degree profiles (empirical distribution of the degrees of neighbors). Before this work, the best known result achieves $\delta=O(1)$ and $n^{o(1)} \leq d \leq n^c$ for some constant $c$ with an $n^{O(\log n)}$-time algorithm \cite{barak2018nearly} and $\delta=\tilde O((d/n)^4)$ and $d = \tilde{\Omega}(n^{4/5})$ with a polynomial-time algorithm \cite{dai2018performance}.

Concept Learning through Deep Reinforcement Learning with Memory-Augmented Neural Networks

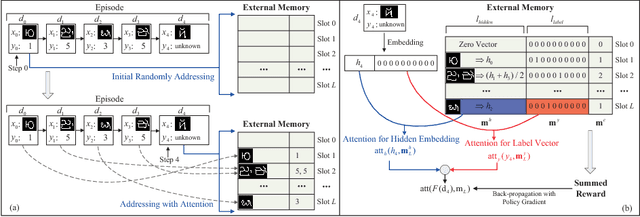
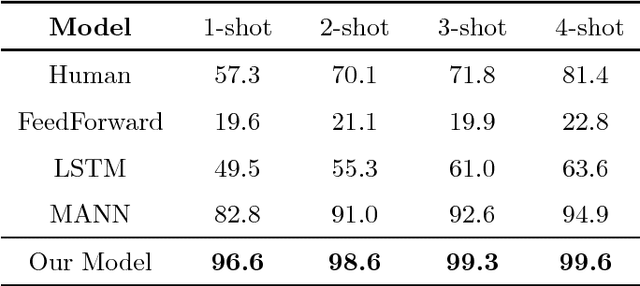
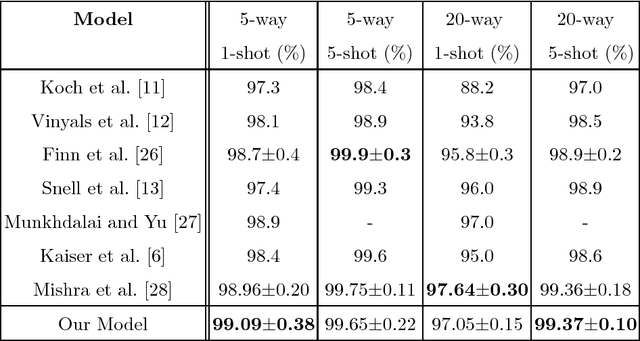
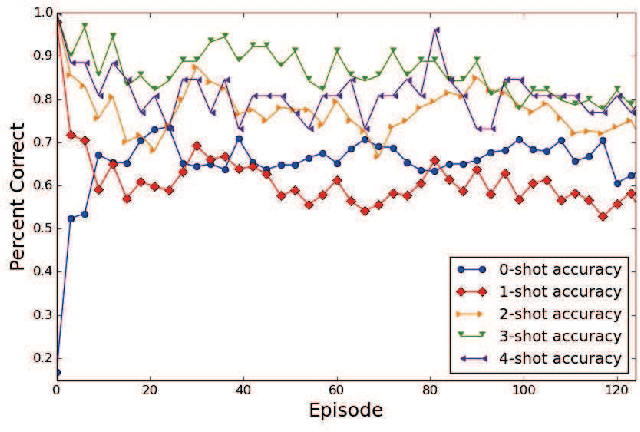
Deep neural networks have shown superior performance in many regimes to remember familiar patterns with large amounts of data. However, the standard supervised deep learning paradigm is still limited when facing the need to learn new concepts efficiently from scarce data. In this paper, we present a memory-augmented neural network which is motivated by the process of human concept learning. The training procedure, imitating the concept formation course of human, learns how to distinguish samples from different classes and aggregate samples of the same kind. In order to better utilize the advantages originated from the human behavior, we propose a sequential process, during which the network should decide how to remember each sample at every step. In this sequential process, a stable and interactive memory serves as an important module. We validate our model in some typical one-shot learning tasks and also an exploratory outlier detection problem. In all the experiments, our model gets highly competitive to reach or outperform those strong baselines.

Convex Relaxation Methods for Community Detection

This paper surveys recent theoretical advances in convex optimization approaches for community detection. We introduce some important theoretical techniques and results for establishing the consistency of convex community detection under various statistical models. In particular, we discuss the basic techniques based on the primal and dual analysis. We also present results that demonstrate several distinctive advantages of convex community detection, including robustness against outlier nodes, consistency under weak assortativity, and adaptivity to heterogeneous degrees. This survey is not intended to be a complete overview of the vast literature on this fast-growing topic. Instead, we aim to provide a big picture of the remarkable recent development in this area and to make the survey accessible to a broad audience. We hope that this expository article can serve as an introductory guide for readers who are interested in using, designing, and analyzing convex relaxation methods in network analysis.