Continuous Semi-Implicit Models

Semi-implicit distributions have shown great promise in variational inference and generative modeling. Hierarchical semi-implicit models, which stack multiple semi-implicit layers, enhance the expressiveness of semi-implicit distributions and can be used to accelerate diffusion models given pretrained score networks. However, their sequential training often suffers from slow convergence. In this paper, we introduce CoSIM, a continuous semi-implicit model that extends hierarchical semi-implicit models into a continuous framework. By incorporating a continuous transition kernel, CoSIM enables efficient, simulation-free training. Furthermore, we show that CoSIM achieves consistency with a carefully designed transition kernel, offering a novel approach for multistep distillation of generative models at the distributional level. Extensive experiments on image generation demonstrate that CoSIM performs on par or better than existing diffusion model acceleration methods, achieving superior performance on FD-DINOv2.

Invertible Attention

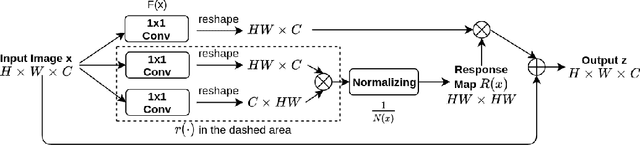
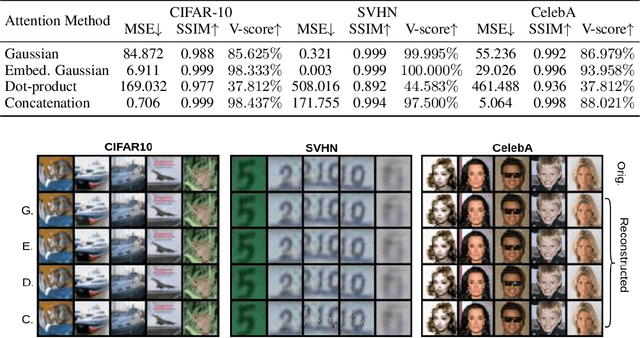
Attention has been proved to be an efficient mechanism to capture long-range dependencies. However, so far it has not been deployed in invertible networks. This is due to the fact that in order to make a network invertible, every component within the network needs to be a bijective transformation, but a normal attention block is not. In this paper, we propose invertible attention that can be plugged into existing invertible models. We mathematically and experimentally prove that the invertibility of an attention model can be achieved by carefully constraining its Lipschitz constant. We validate the invertibility of our invertible attention on image reconstruction task with 3 popular datasets: CIFAR-10, SVHN, and CelebA. We also show that our invertible attention achieves similar performance in comparison with normal non-invertible attention on dense prediction tasks. The code is available at https://github.com/Schwartz-Zha/InvertibleAttention