Decoupled Geometric Parameterization and its Application in Deep Homography Estimation

Planar homography, with eight degrees of freedom (DOFs), is fundamental in numerous computer vision tasks. While the positional offsets of four corners are widely adopted (especially in neural network predictions), this parameterization lacks geometric interpretability and typically requires solving a linear system to compute the homography matrix. This paper presents a novel geometric parameterization of homographies, leveraging the similarity-kernel-similarity (SKS) decomposition for projective transformations. Two independent sets of four geometric parameters are decoupled: one for a similarity transformation and the other for the kernel transformation. Additionally, the geometric interpretation linearly relating the four kernel transformation parameters to angular offsets is derived. Our proposed parameterization allows for direct homography estimation through matrix multiplication, eliminating the need for solving a linear system, and achieves performance comparable to the four-corner positional offsets in deep homography estimation.

Fast and Interpretable 2D Homography Decomposition: Similarity-Kernel-Similarity and Affine-Core-Affine Transformations

In this paper, we present two fast and interpretable decomposition methods for 2D homography, which are named Similarity-Kernel-Similarity (SKS) and Affine-Core-Affine (ACA) transformations respectively. Under the minimal $4$-point configuration, the first and the last similarity transformations in SKS are computed by two anchor points on target and source planes, respectively. Then, the other two point correspondences can be exploited to compute the middle kernel transformation with only four parameters. Furthermore, ACA uses three anchor points to compute the first and the last affine transformations, followed by computation of the middle core transformation utilizing the other one point correspondence. ACA can compute a homography up to a scale with only $85$ floating-point operations (FLOPs), without even any division operations. Therefore, as a plug-in module, ACA facilitates the traditional feature-based Random Sample Consensus (RANSAC) pipeline, as well as deep homography pipelines estimating $4$-point offsets. In addition to the advantages of geometric parameterization and computational efficiency, SKS and ACA can express each element of homography by a polynomial of input coordinates ($7$th degree to $9$th degree), extend the existing essential Similarity-Affine-Projective (SAP) decomposition and calculate 2D affine transformations in a unified way. Source codes are released in https://github.com/cscvlab/SKS-Homography.

StackRec: Efficient Training of Very Deep Sequential Recommender Models by Layer Stacking

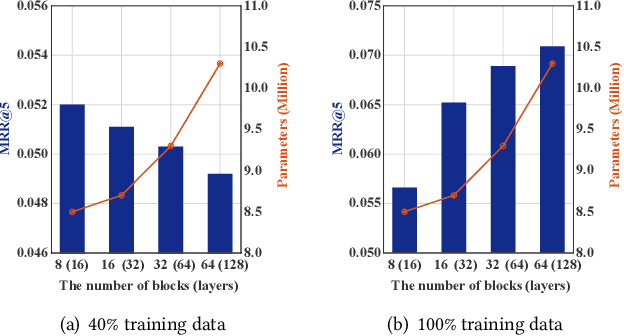
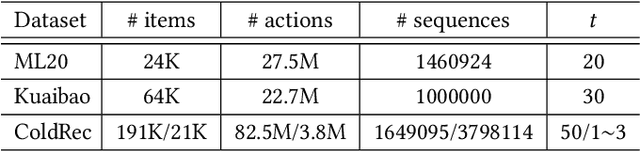
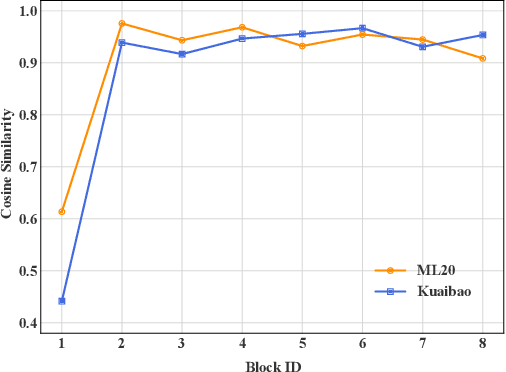
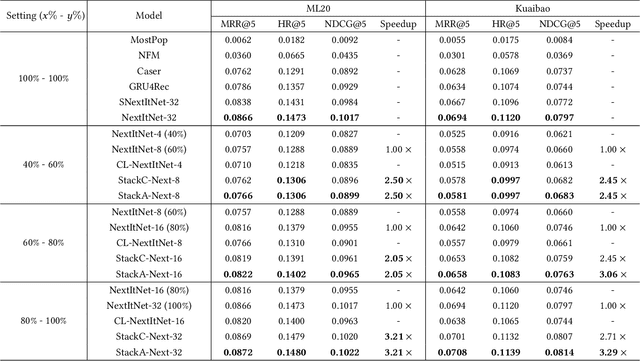
Deep learning has brought great progress for the sequential recommendation (SR) tasks. With the structure of advanced residual networks, sequential recommender models can be stacked with many hidden layers, e.g., up to 100 layers on real-world SR datasets. Training such a deep network requires expensive computation and longer training time, especially in situations when there are tens of billions of user-item interactions. To deal with such a challenge, we present StackRec, a simple but very efficient training framework for deep SR models by layer stacking. Specifically, we first offer an important insight that residual layers/blocks in a well-trained deep SR model have similar distribution. Enlightened by this, we propose progressively stacking such pre-trained residual layers/blocks so as to yield a deeper but easier-to-train SR model. We validate the proposed StackRec by instantiating with two state-of-the-art SR models in three practical scenarios and real-world datasets. Extensive experiments show that StackRec achieves not only comparable performance, but also significant acceleration in training time, compared to SR models that are trained from scratch.