Itay Evron
Optimal L2 Regularization in High-dimensional Continual Linear Regression
Jan 20, 2026Abstract:We study generalization in an overparameterized continual linear regression setting, where a model is trained with L2 (isotropic) regularization across a sequence of tasks. We derive a closed-form expression for the expected generalization loss in the high-dimensional regime that holds for arbitrary linear teachers. We demonstrate that isotropic regularization mitigates label noise under both single-teacher and multiple i.i.d. teacher settings, whereas prior work accommodating multiple teachers either did not employ regularization or used memory-demanding methods. Furthermore, we prove that the optimal fixed regularization strength scales nearly linearly with the number of tasks $T$, specifically as $T/\ln T$. To our knowledge, this is the first such result in theoretical continual learning. Finally, we validate our theoretical findings through experiments on linear regression and neural networks, illustrating how this scaling law affects generalization and offering a practical recipe for the design of continual learning systems.
Optimal Rates in Continual Linear Regression via Increasing Regularization
Jun 06, 2025Abstract:We study realizable continual linear regression under random task orderings, a common setting for developing continual learning theory. In this setup, the worst-case expected loss after $k$ learning iterations admits a lower bound of $\Omega(1/k)$. However, prior work using an unregularized scheme has only established an upper bound of $O(1/k^{1/4})$, leaving a significant gap. Our paper proves that this gap can be narrowed, or even closed, using two frequently used regularization schemes: (1) explicit isotropic $\ell_2$ regularization, and (2) implicit regularization via finite step budgets. We show that these approaches, which are used in practice to mitigate forgetting, reduce to stochastic gradient descent (SGD) on carefully defined surrogate losses. Through this lens, we identify a fixed regularization strength that yields a near-optimal rate of $O(\log k / k)$. Moreover, formalizing and analyzing a generalized variant of SGD for time-varying functions, we derive an increasing regularization strength schedule that provably achieves an optimal rate of $O(1/k)$. This suggests that schedules that increase the regularization coefficient or decrease the number of steps per task are beneficial, at least in the worst case.
Better Rates for Random Task Orderings in Continual Linear Models
Apr 06, 2025


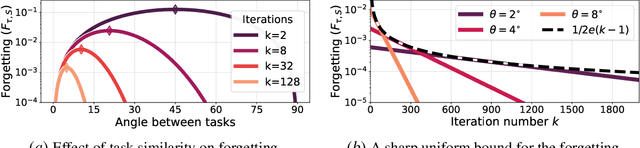
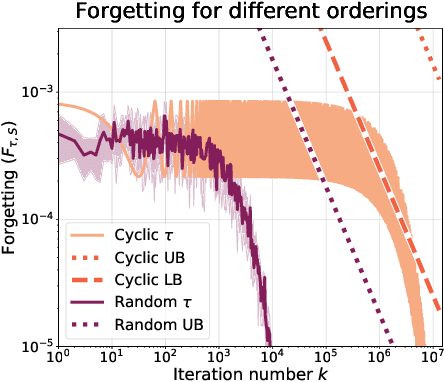
Abstract:We study the common continual learning setup where an overparameterized model is sequentially fitted to a set of jointly realizable tasks. We analyze the forgetting, i.e., loss on previously seen tasks, after $k$ iterations. For linear models, we prove that fitting a task is equivalent to a single stochastic gradient descent (SGD) step on a modified objective. We develop novel last-iterate SGD upper bounds in the realizable least squares setup, and apply them to derive new results for continual learning. Focusing on random orderings over $T$ tasks, we establish universal forgetting rates, whereas existing rates depend on the problem dimensionality or complexity. Specifically, in continual regression with replacement, we improve the best existing rate from $O((d-r)/k)$ to $O(\min(k^{-1/4}, \sqrt{d-r}/k, \sqrt{Tr}/k))$, where $d$ is the dimensionality and $r$ the average task rank. Furthermore, we establish the first rates for random task orderings without replacement. The obtained rate of $O(\min(T^{-1/4}, (d-r)/T))$ proves for the first time that randomization alone, with no task repetition, can prevent catastrophic forgetting in sufficiently long task sequences. Finally, we prove a similar $O(k^{-1/4})$ universal rate for the forgetting in continual linear classification on separable data. Our universal rates apply for broader projection methods, such as block Kaczmarz and POCS, illuminating their loss convergence under i.i.d and one-pass orderings.
Provable Tempered Overfitting of Minimal Nets and Typical Nets
Oct 24, 2024


Abstract:We study the overfitting behavior of fully connected deep Neural Networks (NNs) with binary weights fitted to perfectly classify a noisy training set. We consider interpolation using both the smallest NN (having the minimal number of weights) and a random interpolating NN. For both learning rules, we prove overfitting is tempered. Our analysis rests on a new bound on the size of a threshold circuit consistent with a partial function. To the best of our knowledge, ours are the first theoretical results on benign or tempered overfitting that: (1) apply to deep NNs, and (2) do not require a very high or very low input dimension.
The Joint Effect of Task Similarity and Overparameterization on Catastrophic Forgetting -- An Analytical Model
Jan 24, 2024Abstract:In continual learning, catastrophic forgetting is affected by multiple aspects of the tasks. Previous works have analyzed separately how forgetting is affected by either task similarity or overparameterization. In contrast, our paper examines how task similarity and overparameterization jointly affect forgetting in an analyzable model. Specifically, we focus on two-task continual linear regression, where the second task is a random orthogonal transformation of an arbitrary first task (an abstraction of random permutation tasks). We derive an exact analytical expression for the expected forgetting - and uncover a nuanced pattern. In highly overparameterized models, intermediate task similarity causes the most forgetting. However, near the interpolation threshold, forgetting decreases monotonically with the expected task similarity. We validate our findings with linear regression on synthetic data, and with neural networks on established permutation task benchmarks.
Continual Learning in Linear Classification on Separable Data
Jun 06, 2023Abstract:We analyze continual learning on a sequence of separable linear classification tasks with binary labels. We show theoretically that learning with weak regularization reduces to solving a sequential max-margin problem, corresponding to a special case of the Projection Onto Convex Sets (POCS) framework. We then develop upper bounds on the forgetting and other quantities of interest under various settings with recurring tasks, including cyclic and random orderings of tasks. We discuss several practical implications to popular training practices like regularization scheduling and weighting. We point out several theoretical differences between our continual classification setting and a recently studied continual regression setting.
The Role of Codeword-to-Class Assignments in Error-Correcting Codes: An Empirical Study
Feb 10, 2023Abstract:Error-correcting codes (ECC) are used to reduce multiclass classification tasks to multiple binary classification subproblems. In ECC, classes are represented by the rows of a binary matrix, corresponding to codewords in a codebook. Codebooks are commonly either predefined or problem dependent. Given predefined codebooks, codeword-to-class assignments are traditionally overlooked, and codewords are implicitly assigned to classes arbitrarily. Our paper shows that these assignments play a major role in the performance of ECC. Specifically, we examine similarity-preserving assignments, where similar codewords are assigned to similar classes. Addressing a controversy in existing literature, our extensive experiments confirm that similarity-preserving assignments induce easier subproblems and are superior to other assignment policies in terms of their generalization performance. We find that similarity-preserving assignments make predefined codebooks become problem-dependent, without altering other favorable codebook properties. Finally, we show that our findings can improve predefined codebooks dedicated to extreme classification.
How catastrophic can catastrophic forgetting be in linear regression?
May 25, 2022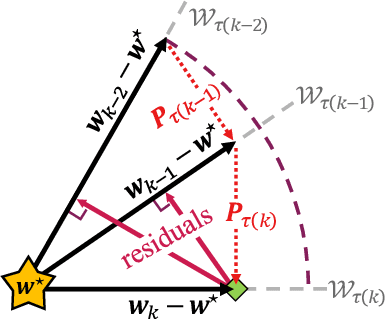
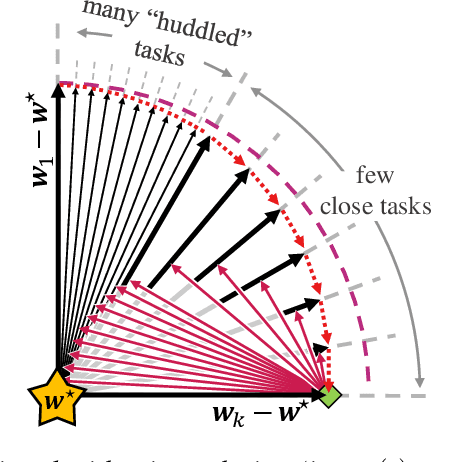
Abstract:To better understand catastrophic forgetting, we study fitting an overparameterized linear model to a sequence of tasks with different input distributions. We analyze how much the model forgets the true labels of earlier tasks after training on subsequent tasks, obtaining exact expressions and bounds. We establish connections between continual learning in the linear setting and two other research areas: alternating projections and the Kaczmarz method. In specific settings, we highlight differences between forgetting and convergence to the offline solution as studied in those areas. In particular, when T tasks in d dimensions are presented cyclically for k iterations, we prove an upper bound of T^2 * min{1/sqrt(k), d/k} on the forgetting. This stands in contrast to the convergence to the offline solution, which can be arbitrarily slow according to existing alternating projection results. We further show that the T^2 factor can be lifted when tasks are presented in a random ordering.
Towards Learning of Filter-Level Heterogeneous Compression of Convolutional Neural Networks
Apr 29, 2019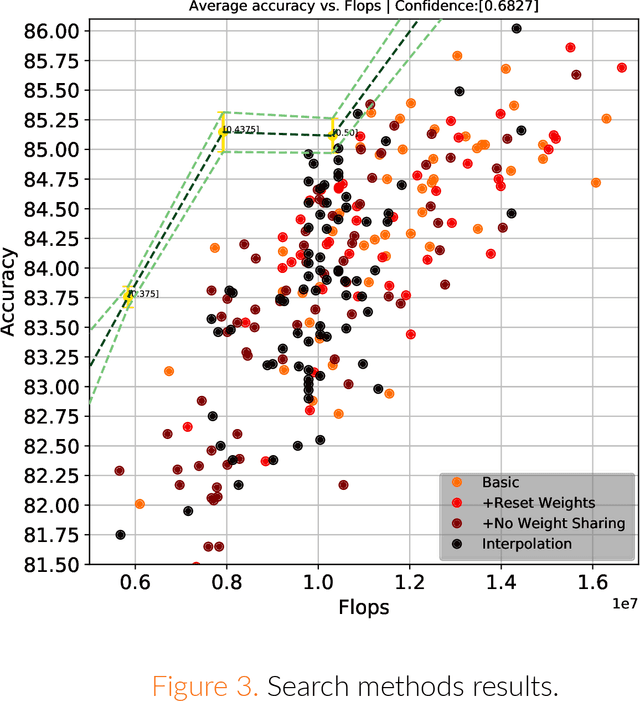
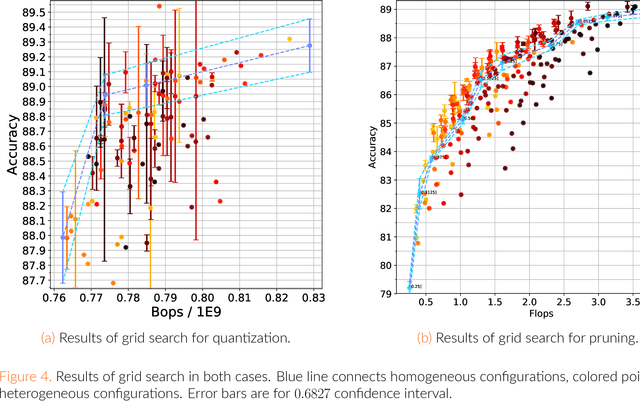
Abstract:Recently, deep learning has become a de facto standard in machine learning with convolutional neural networks (CNNs) demonstrating spectacular success on a wide variety of tasks. However, CNNs are typically very demanding computationally at inference time. One of the ways to alleviate this burden on certain hardware platforms is quantization relying on the use of low-precision arithmetic representation for the weights and the activations. Another popular method is the pruning of the number of filters in each layer. While mainstream deep learning methods train the neural networks weights while keeping the network architecture fixed, the emerging neural architecture search (NAS) techniques make the latter also amenable to training. In this paper, we formulate optimal arithmetic bit length allocation and neural network pruning as a NAS problem, searching for the configurations satisfying a computational complexity budget while maximizing the accuracy. We use a differentiable search method based on the continuous relaxation of the search space proposed by Liu et al. (arXiv:1806.09055). We show, by grid search, that heterogeneous quantized networks suffer from a high variance which renders the benefit of the search questionable. For pruning, improvement over homogeneous cases is possible, but it is still challenging to find those configurations with the proposed method. The code is publicly available at https://github.com/yochaiz/Slimmable and https://github.com/yochaiz/darts-UNIQ
How do infinite width bounded norm networks look in function space?
Feb 13, 2019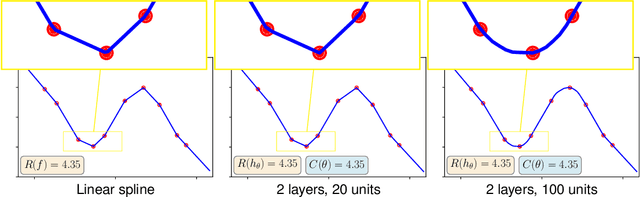
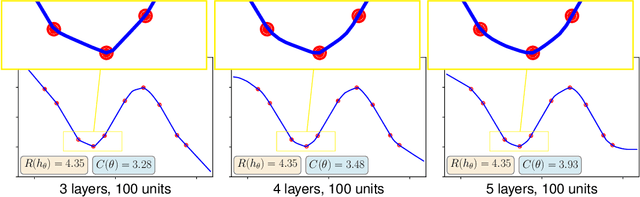
Abstract:We consider the question of what functions can be captured by ReLU networks with an unbounded number of units (infinite width), but where the overall network Euclidean norm (sum of squares of all weights in the system, except for an unregularized bias term for each unit) is bounded; or equivalently what is the minimal norm required to approximate a given function. For functions $f : \mathbb R \rightarrow \mathbb R$ and a single hidden layer, we show that the minimal network norm for representing $f$ is $\max(\int |f''(x)| dx, |f'(-\infty) + f'(+\infty)|)$, and hence the minimal norm fit for a sample is given by a linear spline interpolation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge