Optimal Rates in Continual Linear Regression via Increasing Regularization

We study realizable continual linear regression under random task orderings, a common setting for developing continual learning theory. In this setup, the worst-case expected loss after $k$ learning iterations admits a lower bound of $\Omega(1/k)$. However, prior work using an unregularized scheme has only established an upper bound of $O(1/k^{1/4})$, leaving a significant gap. Our paper proves that this gap can be narrowed, or even closed, using two frequently used regularization schemes: (1) explicit isotropic $\ell_2$ regularization, and (2) implicit regularization via finite step budgets. We show that these approaches, which are used in practice to mitigate forgetting, reduce to stochastic gradient descent (SGD) on carefully defined surrogate losses. Through this lens, we identify a fixed regularization strength that yields a near-optimal rate of $O(\log k / k)$. Moreover, formalizing and analyzing a generalized variant of SGD for time-varying functions, we derive an increasing regularization strength schedule that provably achieves an optimal rate of $O(1/k)$. This suggests that schedules that increase the regularization coefficient or decrease the number of steps per task are beneficial, at least in the worst case.

Multiclass Loss Geometry Matters for Generalization of Gradient Descent in Separable Classification

We study the generalization performance of unregularized gradient methods for separable linear classification. While previous work mostly deal with the binary case, we focus on the multiclass setting with $k$ classes and establish novel population risk bounds for Gradient Descent for loss functions that decay to zero. In this setting, we show risk bounds that reveal that convergence rates are crucially influenced by the geometry of the loss template, as formalized by Wang and Scott (2024), rather than of the loss function itself. Particularly, we establish risk upper bounds that holds for any decay rate of the loss whose template is smooth with respect to the $p$-norm. In the case of exponentially decaying losses, our results indicates a contrast between the $p=\infty$ case, where the risk exhibits a logarithmic dependence on $k$, and $p=2$ where the risk scales linearly with $k$. To establish this separation formally, we also prove a lower bound in the latter scenario, demonstrating that the polynomial dependence on $k$ is unavoidable. Central to our analysis is a novel bound on the Rademacher complexity of low-noise vector-valued linear predictors with a loss template smooth w.r.t.~general $p$-norms.

Better Rates for Random Task Orderings in Continual Linear Models

We study the common continual learning setup where an overparameterized model is sequentially fitted to a set of jointly realizable tasks. We analyze the forgetting, i.e., loss on previously seen tasks, after $k$ iterations. For linear models, we prove that fitting a task is equivalent to a single stochastic gradient descent (SGD) step on a modified objective. We develop novel last-iterate SGD upper bounds in the realizable least squares setup, and apply them to derive new results for continual learning. Focusing on random orderings over $T$ tasks, we establish universal forgetting rates, whereas existing rates depend on the problem dimensionality or complexity. Specifically, in continual regression with replacement, we improve the best existing rate from $O((d-r)/k)$ to $O(\min(k^{-1/4}, \sqrt{d-r}/k, \sqrt{Tr}/k))$, where $d$ is the dimensionality and $r$ the average task rank. Furthermore, we establish the first rates for random task orderings without replacement. The obtained rate of $O(\min(T^{-1/4}, (d-r)/T))$ proves for the first time that randomization alone, with no task repetition, can prevent catastrophic forgetting in sufficiently long task sequences. Finally, we prove a similar $O(k^{-1/4})$ universal rate for the forgetting in continual linear classification on separable data. Our universal rates apply for broader projection methods, such as block Kaczmarz and POCS, illuminating their loss convergence under i.i.d and one-pass orderings.

Complexity of Vector-valued Prediction: From Linear Models to Stochastic Convex Optimization

We study the problem of learning vector-valued linear predictors: these are prediction rules parameterized by a matrix that maps an $m$-dimensional feature vector to a $k$-dimensional target. We focus on the fundamental case with a convex and Lipschitz loss function, and show several new theoretical results that shed light on the complexity of this problem and its connection to related learning models. First, we give a tight characterization of the sample complexity of Empirical Risk Minimization (ERM) in this setting, establishing that $\smash{\widetilde{\Omega}}(k/\epsilon^2)$ examples are necessary for ERM to reach $\epsilon$ excess (population) risk; this provides for an exponential improvement over recent results by Magen and Shamir (2023) in terms of the dependence on the target dimension $k$, and matches a classical upper bound due to Maurer (2016). Second, we present a black-box conversion from general $d$-dimensional Stochastic Convex Optimization (SCO) to vector-valued linear prediction, showing that any SCO problem can be embedded as a prediction problem with $k=\Theta(d)$ outputs. These results portray the setting of vector-valued linear prediction as bridging between two extensively studied yet disparate learning models: linear models (corresponds to $k=1$) and general $d$-dimensional SCO (with $k=\Theta(d)$).

The Dimension Strikes Back with Gradients: Generalization of Gradient Methods in Stochastic Convex Optimization

We study the generalization performance of gradient methods in the fundamental stochastic convex optimization setting, focusing on its dimension dependence. First, for full-batch gradient descent (GD) we give a construction of a learning problem in dimension $d=O(n^2)$, where the canonical version of GD (tuned for optimal performance of the empirical risk) trained with $n$ training examples converges, with constant probability, to an approximate empirical risk minimizer with $\Omega(1)$ population excess risk. Our bound translates to a lower bound of $\Omega (\sqrt{d})$ on the number of training examples required for standard GD to reach a non-trivial test error, answering an open question raised by Feldman (2016) and Amir, Koren, and Livni (2021b) and showing that a non-trivial dimension dependence is unavoidable. Furthermore, for standard one-pass stochastic gradient descent (SGD), we show that an application of the same construction technique provides a similar $\Omega(\sqrt{d})$ lower bound for the sample complexity of SGD to reach a non-trivial empirical error, despite achieving optimal test performance. This again provides an exponential improvement in the dimension dependence compared to previous work (Koren, Livni, Mansour, and Sherman, 2022), resolving an open question left therein.

Tight Risk Bounds for Gradient Descent on Separable Data

We study the generalization properties of unregularized gradient methods applied to separable linear classification -- a setting that has received considerable attention since the pioneering work of Soudry et al. (2018). We establish tight upper and lower (population) risk bounds for gradient descent in this setting, for any smooth loss function, expressed in terms of its tail decay rate. Our bounds take the form $\Theta(r_{\ell,T}^2 / \gamma^2 T + r_{\ell,T}^2 / \gamma^2 n)$, where $T$ is the number of gradient steps, $n$ is size of the training set, $\gamma$ is the data margin, and $r_{\ell,T}$ is a complexity term that depends on the (tail decay rate) of the loss function (and on $T$). Our upper bound matches the best known upper bounds due to Shamir (2021); Schliserman and Koren (2022), while extending their applicability to virtually any smooth loss function and relaxing technical assumptions they impose. Our risk lower bounds are the first in this context and establish the tightness of our upper bounds for any given tail decay rate and in all parameter regimes. The proof technique used to show these results is also markedly simpler compared to previous work, and is straightforward to extend to other gradient methods; we illustrate this by providing analogous results for Stochastic Gradient Descent.

Stability vs Implicit Bias of Gradient Methods on Separable Data and Beyond

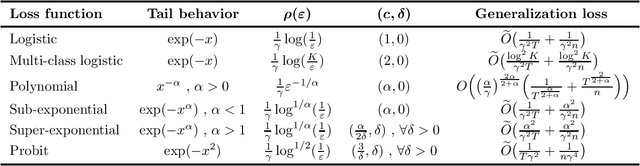
An influential line of recent work has focused on the generalization properties of unregularized gradient-based learning procedures applied to separable linear classification with exponentially-tailed loss functions. The ability of such methods to generalize well has been attributed to the their implicit bias towards large margin predictors, both asymptotically as well as in finite time. We give an additional unified explanation for this generalization and relate it to two simple properties of the optimization objective, that we refer to as realizability and self-boundedness. We introduce a general setting of unconstrained stochastic convex optimization with these properties, and analyze generalization of gradient methods through the lens of algorithmic stability. In this broader setting, we obtain sharp stability bounds for gradient descent and stochastic gradient descent which apply even for a very large number of gradient steps, and use them to derive general generalization bounds for these algorithms. Finally, as direct applications of the general bounds, we return to the setting of linear classification with separable data and establish several novel test loss and test accuracy bounds for gradient descent and stochastic gradient descent for a variety of loss functions with different tail decay rates. In some of these case, our bounds significantly improve upon the existing generalization error bounds in the literature.