Zero Inflation as a Missing Data Problem: a Proxy-based Approach

A common type of zero-inflated data has certain true values incorrectly replaced by zeros due to data recording conventions (rare outcomes assumed to be absent) or details of data recording equipment (e.g. artificial zeros in gene expression data). Existing methods for zero-inflated data either fit the observed data likelihood via parametric mixture models that explicitly represent excess zeros, or aim to replace excess zeros by imputed values. If the goal of the analysis relies on knowing true data realizations, a particular challenge with zero-inflated data is identifiability, since it is difficult to correctly determine which observed zeros are real and which are inflated. This paper views zero-inflated data as a general type of missing data problem, where the observability indicator for a potentially censored variable is itself unobserved whenever a zero is recorded. We show that, without additional assumptions, target parameters involving a zero-inflated variable are not identified. However, if a proxy of the missingness indicator is observed, a modification of the effect restoration approach of Kuroki and Pearl allows identification and estimation, given the proxy-indicator relationship is known. If this relationship is unknown, our approach yields a partial identification strategy for sensitivity analysis. Specifically, we show that only certain proxy-indicator relationships are compatible with the observed data distribution. We give an analytic bound for this relationship in cases with a categorical outcome, which is sharp in certain models. For more complex cases, sharp numerical bounds may be computed using methods in Duarte et al.[2023]. We illustrate our method via simulation studies and a data application on central line-associated bloodstream infections (CLABSIs).

An Introduction to Causal Inference Methods for Observational Human-Robot Interaction Research

Quantitative methods in Human-Robot Interaction (HRI) research have primarily relied upon randomized, controlled experiments in laboratory settings. However, such experiments are not always feasible when external validity, ethical constraints, and ease of data collection are of concern. Furthermore, as consumer robots become increasingly available, increasing amounts of real-world data will be available to HRI researchers, which prompts the need for quantative approaches tailored to the analysis of observational data. In this article, we present an alternate approach towards quantitative research for HRI researchers using methods from causal inference that can enable researchers to identify causal relationships in observational settings where randomized, controlled experiments cannot be run. We highlight different scenarios that HRI research with consumer household robots may involve to contextualize how methods from causal inference can be applied to observational HRI research. We then provide a tutorial summarizing key concepts from causal inference using a graphical model perspective and link to code examples throughout the article, which are available at https://gitlab.com/causal/causal_hri. Our work paves the way for further discussion on new approaches towards observational HRI research while providing a starting point for HRI researchers to add causal inference techniques to their analytical toolbox.

Off-Policy Evaluation in Embedded Spaces

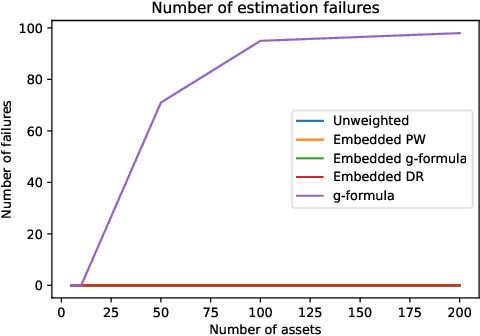
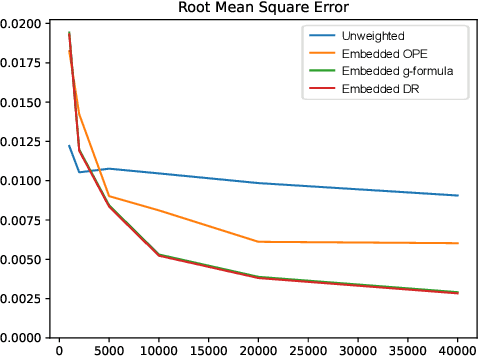
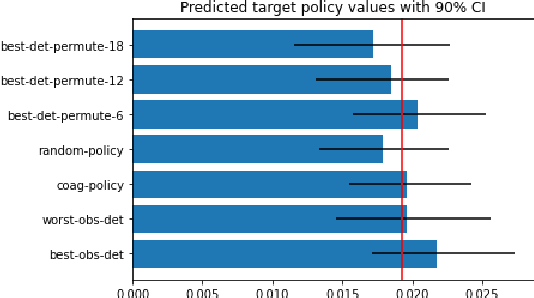
Off-policy evaluation methods are important in recommendation systems and search engines, whereby data collected under an old logging policy is used to predict the performance of a new target policy. However, in practice most systems are not observed to recommend most of the possible actions, which is an issue since existing methods require that the probability of the target policy recommending an item can only be non-zero when the probability of the logging policy is non-zero (known as absolute continuity). To circumvent this issue, we explore the use of action embeddings. By representing contexts and actions in an embedding space, we are able to share information to extrapolate behaviors for actions and contexts previously unseen.

Identification Methods With Arbitrary Interventional Distributions as Inputs

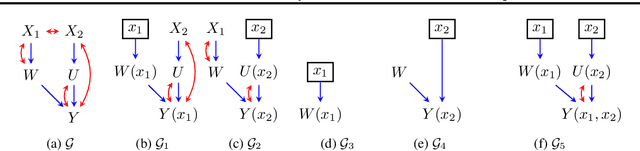
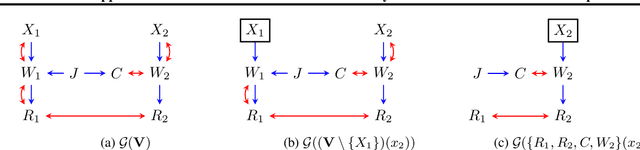
Causal inference quantifies cause-effect relationships by estimating counterfactual parameters from data. This entails using \emph{identification theory} to establish a link between counterfactual parameters of interest and distributions from which data is available. A line of work characterized non-parametric identification for a wide variety of causal parameters in terms of the \emph{observed data distribution}. More recently, identification results have been extended to settings where experimental data from interventional distributions is also available. In this paper, we use Single World Intervention Graphs and a nested factorization of models associated with mixed graphs to give a very simple view of existing identification theory for experimental data. We use this view to yield general identification algorithms for settings where the input distributions consist of an arbitrary set of observational and experimental distributions, including marginal and conditional distributions. We show that for problems where inputs are interventional marginal distributions of a certain type (ancestral marginals), our algorithm is complete.