Federated Unbiased Learning to Rank

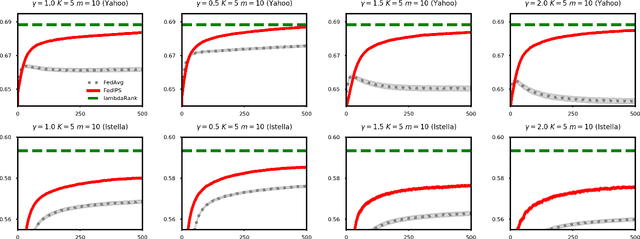
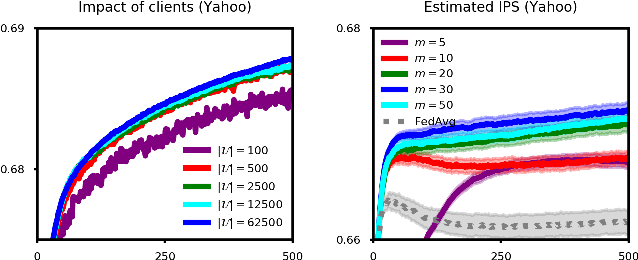
Unbiased Learning to Rank (ULTR) studies the problem of learning a ranking function based on biased user interactions. In this framework, ULTR algorithms have to rely on a large amount of user data that are collected, stored, and aggregated by central servers. In this paper, we consider an on-device search setting, where users search against their personal corpora on their local devices, and the goal is to learn a ranking function from biased user interactions. Due to privacy constraints, users' queries, personal documents, results lists, and raw interaction data will not leave their devices, and ULTR has to be carried out via Federated Learning (FL). Directly applying existing ULTR algorithms on users' devices could suffer from insufficient training data due to the limited amount of local interactions. To address this problem, we propose the FedIPS algorithm, which learns from user interactions on-device under the coordination of a central server and uses click propensities to remove the position bias in user interactions. Our evaluation of FedIPS on the Yahoo and Istella datasets shows that FedIPS is robust over a range of position biases.

Ultra High-Dimensional Nonlinear Feature Selection for Big Biological Data

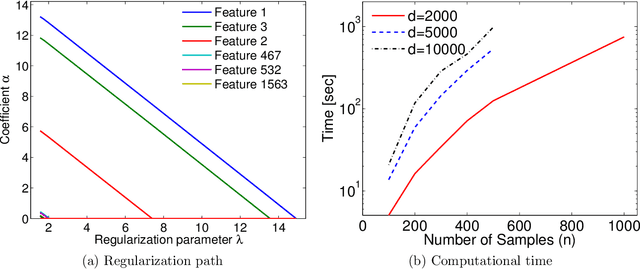
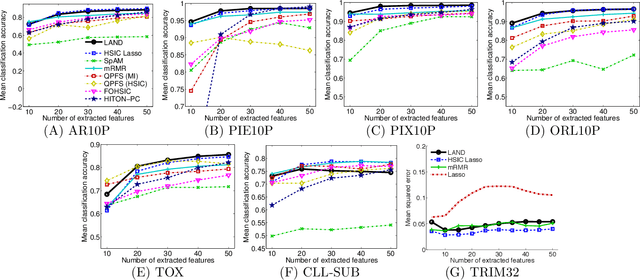
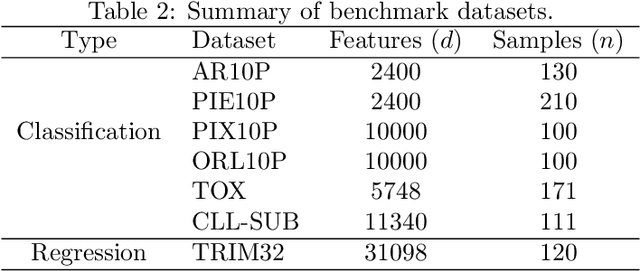
Machine learning methods are used to discover complex nonlinear relationships in biological and medical data. However, sophisticated learning models are computationally unfeasible for data with millions of features. Here we introduce the first feature selection method for nonlinear learning problems that can scale up to large, ultra-high dimensional biological data. More specifically, we scale up the novel Hilbert-Schmidt Independence Criterion Lasso (HSIC Lasso) to handle millions of features with tens of thousand samples. The proposed method is guaranteed to find an optimal subset of maximally predictive features with minimal redundancy, yielding higher predictive power and improved interpretability. Its effectiveness is demonstrated through applications to classify phenotypes based on module expression in human prostate cancer patients and to detect enzymes among protein structures. We achieve high accuracy with as few as 20 out of one million features --- a dimensionality reduction of 99.998%. Our algorithm can be implemented on commodity cloud computing platforms. The dramatic reduction of features may lead to the ubiquitous deployment of sophisticated prediction models in mobile health care applications.

Scaling Submodular Maximization via Pruned Submodularity Graphs

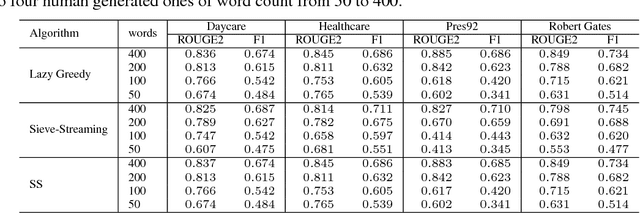
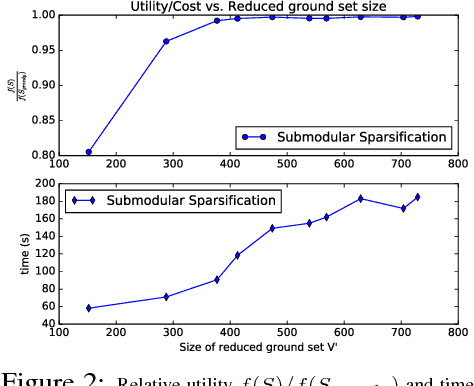
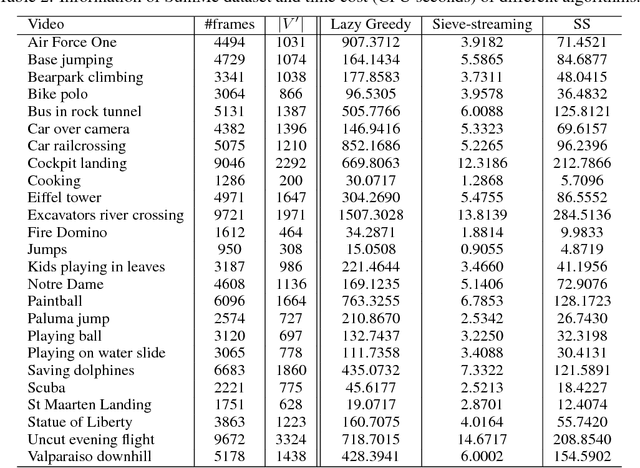
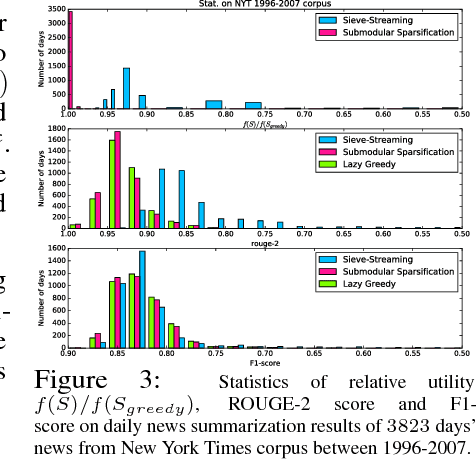
We propose a new random pruning method (called "submodular sparsification (SS)") to reduce the cost of submodular maximization. The pruning is applied via a "submodularity graph" over the $n$ ground elements, where each directed edge is associated with a pairwise dependency defined by the submodular function. In each step, SS prunes a $1-1/\sqrt{c}$ (for $c>1$) fraction of the nodes using weights on edges computed based on only a small number ($O(\log n)$) of randomly sampled nodes. The algorithm requires $\log_{\sqrt{c}}n$ steps with a small and highly parallelizable per-step computation. An accuracy-speed tradeoff parameter $c$, set as $c = 8$, leads to a fast shrink rate $\sqrt{2}/4$ and small iteration complexity $\log_{2\sqrt{2}}n$. Analysis shows that w.h.p., the greedy algorithm on the pruned set of size $O(\log^2 n)$ can achieve a guarantee similar to that of processing the original dataset. In news and video summarization tasks, SS is able to substantially reduce both computational costs and memory usage, while maintaining (or even slightly exceeding) the quality of the original (and much more costly) greedy algorithm.

N$^3$LARS: Minimum Redundancy Maximum Relevance Feature Selection for Large and High-dimensional Data

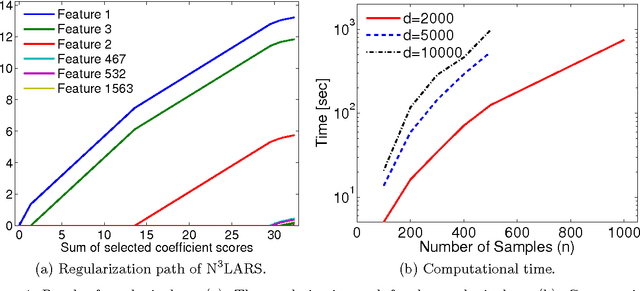
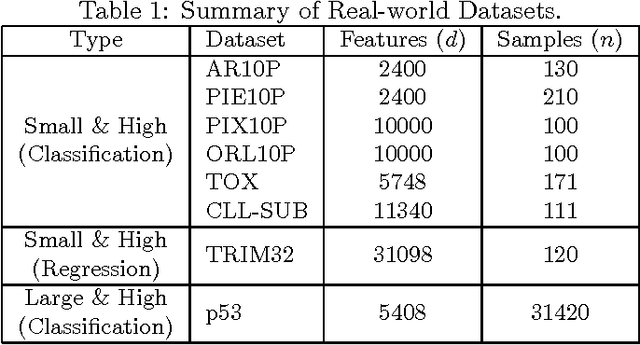
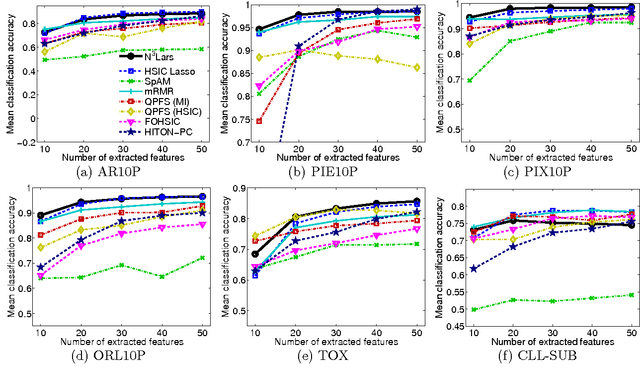
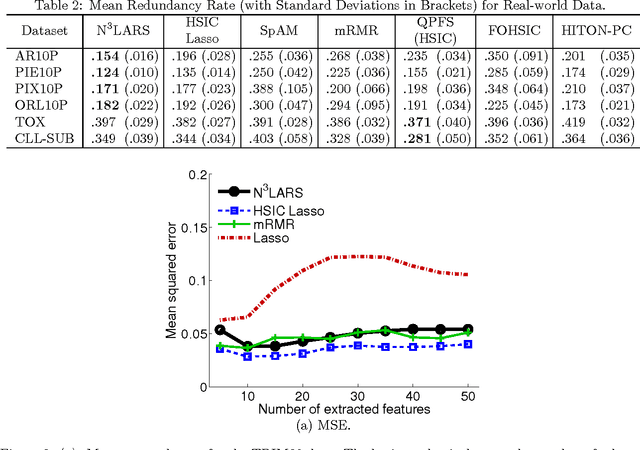
We propose a feature selection method that finds non-redundant features from a large and high-dimensional data in nonlinear way. Specifically, we propose a nonlinear extension of the non-negative least-angle regression (LARS) called N${}^3$LARS, where the similarity between input and output is measured through the normalized version of the Hilbert-Schmidt Independence Criterion (HSIC). An advantage of N${}^3$LARS is that it can easily incorporate with map-reduce frameworks such as Hadoop and Spark. Thus, with the help of distributed computing, a set of features can be efficiently selected from a large and high-dimensional data. Moreover, N${}^3$LARS is a convex method and can find a global optimum solution. The effectiveness of the proposed method is first demonstrated through feature selection experiments for classification and regression with small and high-dimensional datasets. Finally, we evaluate our proposed method over a large and high-dimensional biology dataset.

Stochastic ADMM for Nonsmooth Optimization

We present a stochastic setting for optimization problems with nonsmooth convex separable objective functions over linear equality constraints. To solve such problems, we propose a stochastic Alternating Direction Method of Multipliers (ADMM) algorithm. Our algorithm applies to a more general class of nonsmooth convex functions that does not necessarily have a closed-form solution by minimizing the augmented function directly. We also demonstrate the rates of convergence for our algorithm under various structural assumptions of the stochastic functions: $O(1/\sqrt{t})$ for convex functions and $O(\log t/t)$ for strongly convex functions. Compared to previous literature, we establish the convergence rate of ADMM algorithm, for the first time, in terms of both the objective value and the feasibility violation.

Stochastic Smoothing for Nonsmooth Minimizations: Accelerating SGD by Exploiting Structure

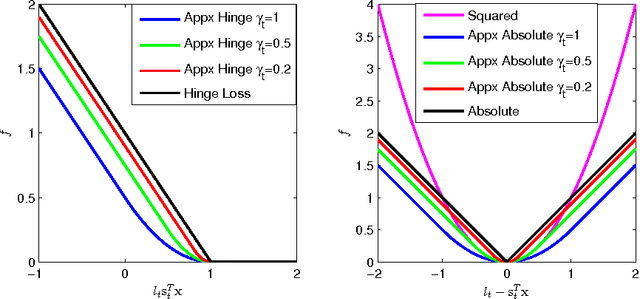
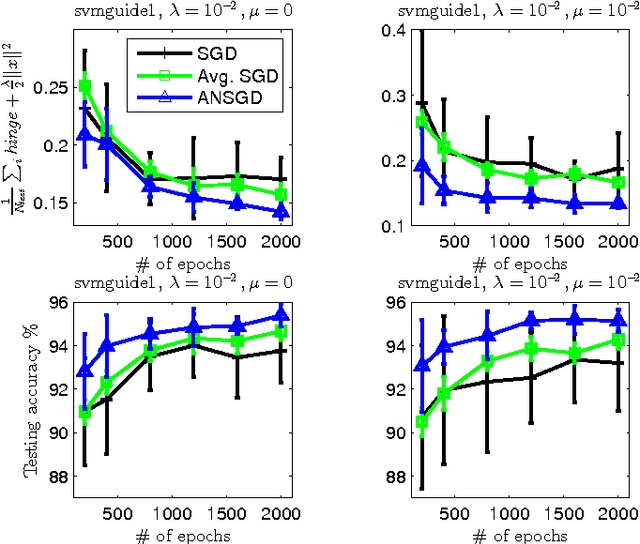
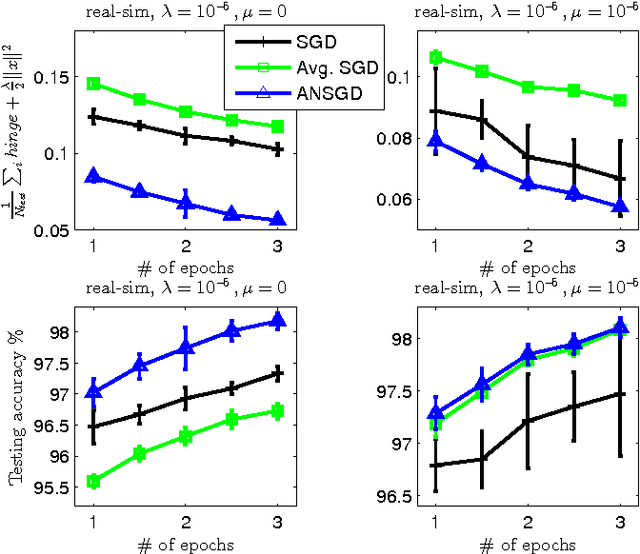
In this work we consider the stochastic minimization of nonsmooth convex loss functions, a central problem in machine learning. We propose a novel algorithm called Accelerated Nonsmooth Stochastic Gradient Descent (ANSGD), which exploits the structure of common nonsmooth loss functions to achieve optimal convergence rates for a class of problems including SVMs. It is the first stochastic algorithm that can achieve the optimal O(1/t) rate for minimizing nonsmooth loss functions (with strong convexity). The fast rates are confirmed by empirical comparisons, in which ANSGD significantly outperforms previous subgradient descent algorithms including SGD.

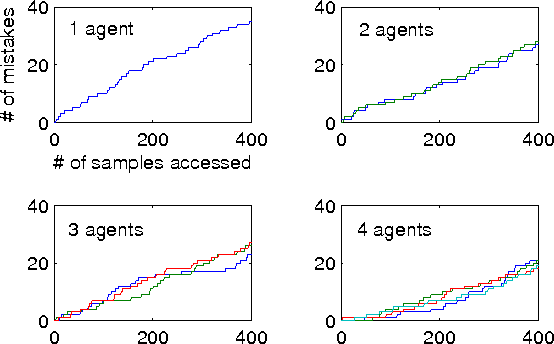
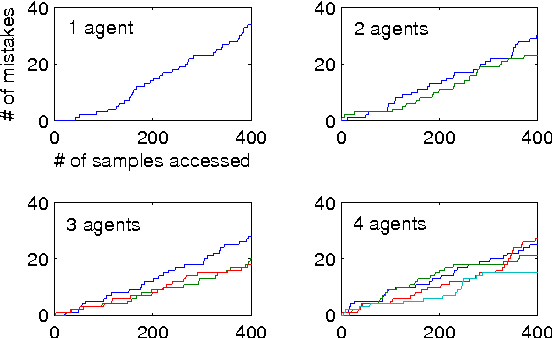
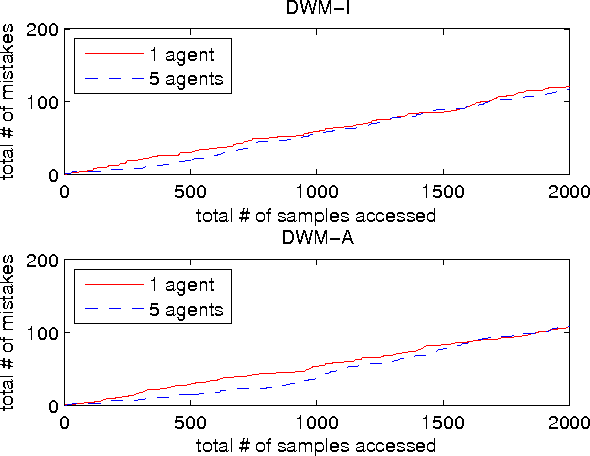
Data-Distributed Weighted Majority and Online Mirror Descent

In this paper, we focus on the question of the extent to which online learning can benefit from distributed computing. We focus on the setting in which $N$ agents online-learn cooperatively, where each agent only has access to its own data. We propose a generic data-distributed online learning meta-algorithm. We then introduce the Distributed Weighted Majority and Distributed Online Mirror Descent algorithms, as special cases. We show, using both theoretical analysis and experiments, that compared to a single agent: given the same computation time, these distributed algorithms achieve smaller generalization errors; and given the same generalization errors, they can be $N$ times faster.