A Differentially Private Clustering Algorithm for Well-Clustered Graphs

We study differentially private (DP) algorithms for recovering clusters in well-clustered graphs, which are graphs whose vertex set can be partitioned into a small number of sets, each inducing a subgraph of high inner conductance and small outer conductance. Such graphs have widespread application as a benchmark in the theoretical analysis of spectral clustering. We provide an efficient ($\epsilon$,$\delta$)-DP algorithm tailored specifically for such graphs. Our algorithm draws inspiration from the recent work of Chen et al., who developed DP algorithms for recovery of stochastic block models in cases where the graph comprises exactly two nearly-balanced clusters. Our algorithm works for well-clustered graphs with $k$ nearly-balanced clusters, and the misclassification ratio almost matches the one of the best-known non-private algorithms. We conduct experimental evaluations on datasets with known ground truth clusters to substantiate the prowess of our algorithm. We also show that any (pure) $\epsilon$-DP algorithm would result in substantial error.

HUGE: Huge Unsupervised Graph Embeddings with TPUs

Graphs are a representation of structured data that captures the relationships between sets of objects. With the ubiquity of available network data, there is increasing industrial and academic need to quickly analyze graphs with billions of nodes and trillions of edges. A common first step for network understanding is Graph Embedding, the process of creating a continuous representation of nodes in a graph. A continuous representation is often more amenable, especially at scale, for solving downstream machine learning tasks such as classification, link prediction, and clustering. A high-performance graph embedding architecture leveraging Tensor Processing Units (TPUs) with configurable amounts of high-bandwidth memory is presented that simplifies the graph embedding problem and can scale to graphs with billions of nodes and trillions of edges. We verify the embedding space quality on real and synthetic large-scale datasets.

Constant matters: Fine-grained Complexity of Differentially Private Continual Observation

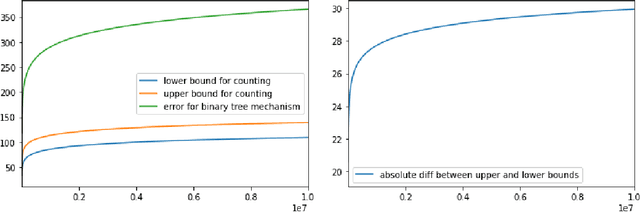
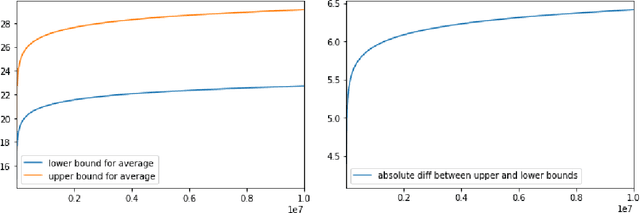
We study fine-grained error bounds for differentially private algorithms for averaging and counting under continual observation. Our main insight is that the factorization mechanism when using lower-triangular matrices, can be used in the continual observation model. We give explicit factorizations for two fundamental matrices, namely the counting matrix $M_{\mathsf{count}}$ and the averaging matrix $M_{\mathsf{average}}$ and show fine-grained bounds for the additive error of the resulting mechanism using the {\em completely bounded norm} (cb-norm) or {\em factorization norm}. Our bound on the cb-norm for $M_{\mathsf{count}}$ is tight up an additive error of 1 and the bound for $M_{\mathsf{average}}$ is tight up to $\approx 0.64$. This allows us to give the first algorithm for averaging whose additive error has $o(\log^{3/2} T)$ dependence. Furthermore, we are the first to give concrete error bounds for various problems under continual observation such as binary counting, maintaining a histogram, releasing an approximately cut-preserving synthetic graph, many graph-based statistics, and substring and episode counting. Finally, we present a fine-grained error bound for non-interactive local learning.

A Theory-Based Evaluation of Nearest Neighbor Models Put Into Practice

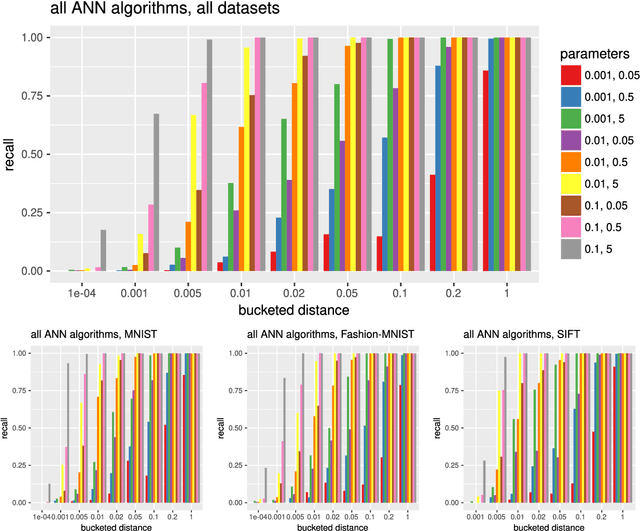
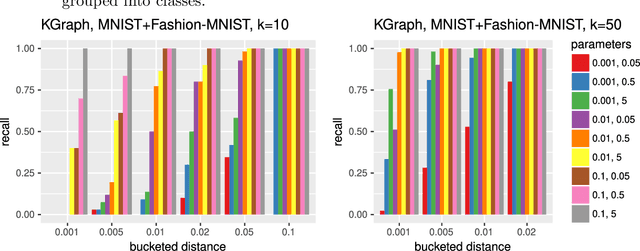
In the $k$-nearest neighborhood model ($k$-NN), we are given a set of points $P$, and we shall answer queries $q$ by returning the $k$ nearest neighbors of $q$ in $P$ according to some metric. This concept is crucial in many areas of data analysis and data processing, e.g., computer vision, document retrieval and machine learning. Many $k$-NN algorithms have been published and implemented, but often the relation between parameters and accuracy of the computed $k$-NN is not explicit. We study property testing of $k$-NN graphs in theory and evaluate it empirically: given a point set $P \subset \mathbb{R}^\delta$ and a directed graph $G=(P,E)$, is $G$ a $k$-NN graph, i.e., every point $p \in P$ has outgoing edges to its $k$ nearest neighbors, or is it $\epsilon$-far from being a $k$-NN graph? Here, $\epsilon$-far means that one has to change more than an $\epsilon$-fraction of the edges in order to make $G$ a $k$-NN graph. We develop a randomized algorithm with one-sided error that decides this question, i.e., a property tester for the $k$-NN property, with complexity $O(\sqrt{n} k^2 / \epsilon^2)$ measured in terms of the number of vertices and edges it inspects, and we prove a lower bound of $\Omega(\sqrt{n / \epsilon k})$. We evaluate our tester empirically on the $k$-NN models computed by various algorithms and show that it can be used to detect $k$-NN models with bad accuracy in significantly less time than the building time of the $k$-NN model.