Multiframe Motion Coupling for Video Super Resolution

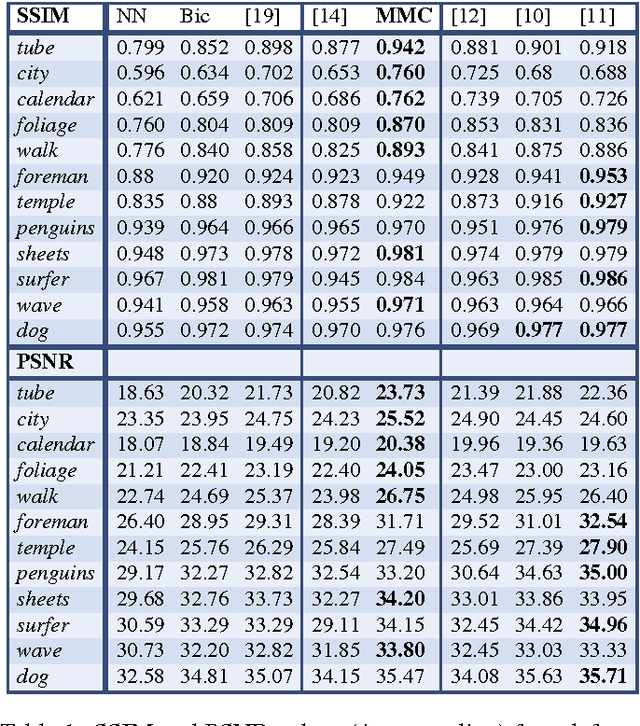
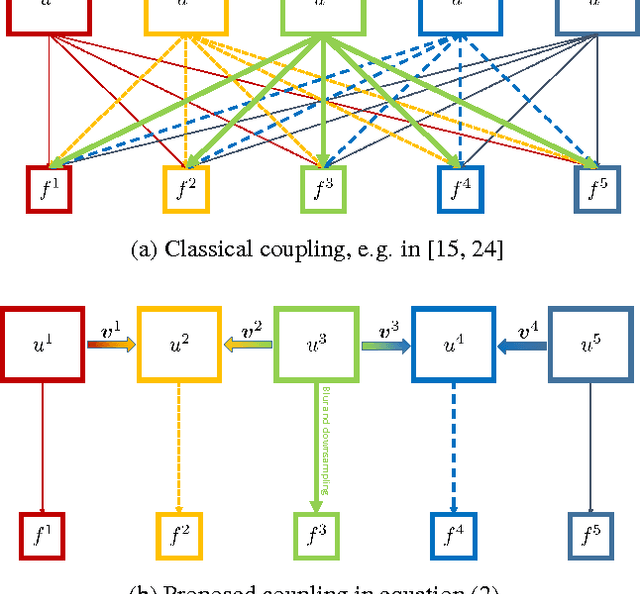
The idea of video super resolution is to use different view points of a single scene to enhance the overall resolution and quality. Classical energy minimization approaches first establish a correspondence of the current frame to all its neighbors in some radius and then use this temporal information for enhancement. In this paper, we propose the first variational super resolution approach that computes several super resolved frames in one batch optimization procedure by incorporating motion information between the high-resolution image frames themselves. As a consequence, the number of motion estimation problems grows linearly in the number of frames, opposed to a quadratic growth of classical methods and temporal consistency is enforced naturally. We use infimal convolution regularization as well as an automatic parameter balancing scheme to automatically determine the reliability of the motion information and reweight the regularization locally. We demonstrate that our approach yields state-of-the-art results and even is competitive with machine learning approaches.

Adaptive Regularization in Convex Composite Optimization for Variational Imaging Problems

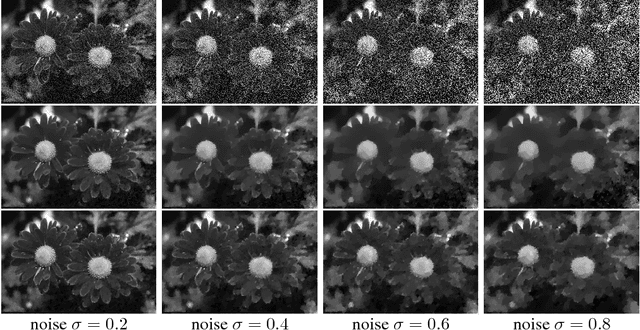
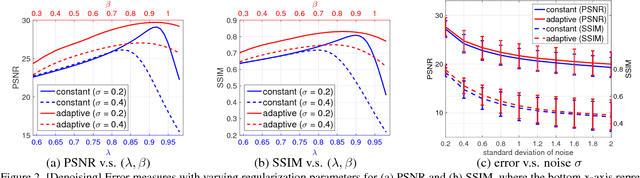
We propose an adaptive regularization scheme in a variational framework where a convex composite energy functional is optimized. We consider a number of imaging problems including denoising, segmentation and motion estimation, which are considered as optimal solutions of the energy functionals that mainly consist of data fidelity, regularization and a control parameter for their trade-off. We presents an algorithm to determine the relative weight between data fidelity and regularization based on the residual that measures how well the observation fits the model. Our adaptive regularization scheme is designed to locally control the regularization at each pixel based on the assumption that the diversity of the residual of a given imaging model spatially varies. The energy optimization is presented in the alternating direction method of multipliers (ADMM) framework where the adaptive regularization is iteratively applied along with mathematical analysis of the proposed algorithm. We demonstrate the robustness and effectiveness of our adaptive regularization through experimental results presenting that the qualitative and quantitative evaluation results of each imaging task are superior to the results with a constant regularization scheme. The desired properties, robustness and effectiveness, of the regularization parameter selection in a variational framework for imaging problems are achieved by merely replacing the static regularization parameter with our adaptive one.

Joint Large-Scale Motion Estimation and Image Reconstruction

This article describes the implementation of the joint motion estimation and image reconstruction framework presented by Burger, Dirks and Sch\"onlieb and extends this framework to large-scale motion between consecutive image frames. The variational framework uses displacements between consecutive frames based on the optical flow approach to improve the image reconstruction quality on the one hand and the motion estimation quality on the other. The energy functional consists of a data-fidelity term with a general operator that connects the input sequence to the solution, it has a total variation term for the image sequence and is connected to the underlying flow using an optical flow term. Additional spatial regularity for the flow is modeled by a total variation regularizer for both components of the flow. The numerical minimization is performed in an alternating manner using primal-dual techniques. The resulting schemes are presented as pseudo-code together with a short numerical evaluation.

A Flexible Primal-Dual Toolbox

\textbf{FlexBox} is a flexible MATLAB toolbox for finite dimensional convex variational problems in image processing and beyond. Such problems often consist of non-differentiable parts and involve linear operators. The toolbox uses a primal-dual scheme to avoid (computationally) inefficient operator inversion and to get reliable error estimates. From the user-side, \textbf{FlexBox} expects the primal formulation of the problem, automatically decouples operators and dualizes the problem. For large-scale problems, \textbf{FlexBox} also comes with a \cpp-module, which can be used stand-alone or together with MATLAB via MEX-interfaces. Besides various pre-implemented data-fidelities and regularization-terms, \textbf{FlexBox} is able to handle arbitrary operators while being easily extendable, due to its object-oriented design. The toolbox is available at \href{http://www.flexbox.im}{http://www.flexbox.im}

A Variational Model for Joint Motion Estimation and Image Reconstruction

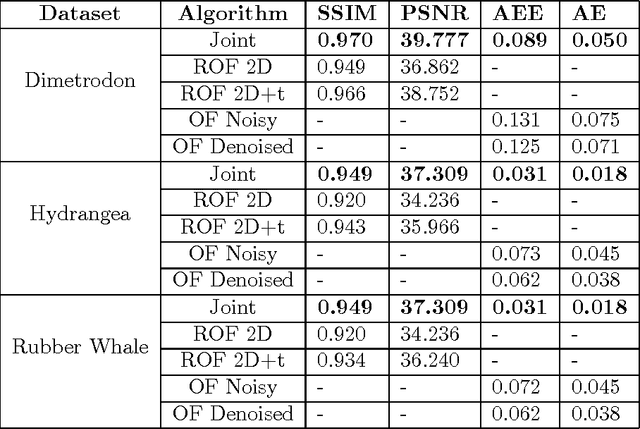
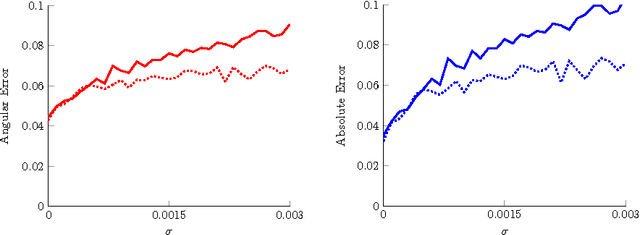
The aim of this paper is to derive and analyze a variational model for the joint estimation of motion and reconstruction of image sequences, which is based on a time-continuous Eulerian motion model. The model can be set up in terms of the continuity equation or the brightness constancy equation. The analysis in this paper focuses on the latter for robust motion estimation on sequences of two-dimensional images. We rigorously prove the existence of a minimizer in a suitable function space setting. Moreover, we discuss the numerical solution of the model based on primal-dual algorithms and investigate several examples. Finally, the benefits of our model compared to existing techniques, such as sequential image reconstruction and motion estimation, are shown.

On Optical Flow Models for Variational Motion Estimation

The aim of this paper is to discuss and evaluate total variation based regularization methods for motion estimation, with particular focus on optical flow models. In addition to standard $L^2$ and $L^1$ data fidelities we give an overview of different variants of total variation regularization obtained from combination with higher order models and a unified computational optimization approach based on primal-dual methods. Moreover, we extend the models by Bregman iterations and provide an inverse problems perspective to the analysis of variational optical flow models. A particular focus of the paper is the quantitative evaluation of motion estimation, which is a difficult and often underestimated task. We discuss several approaches for quality measures of motion estimation and apply them to compare the previously discussed regularization approaches.