Adaptive Regularization of Some Inverse Problems in Image Analysis

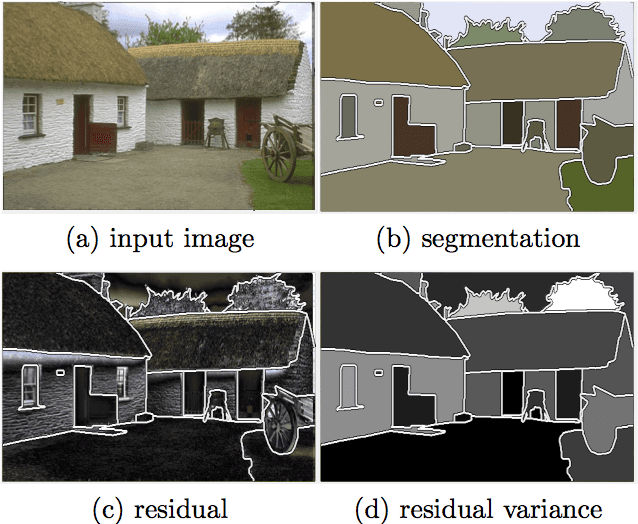
We present an adaptive regularization scheme for optimizing composite energy functionals arising in image analysis problems. The scheme automatically trades off data fidelity and regularization depending on the current data fit during the iterative optimization, so that regularization is strongest initially, and wanes as data fidelity improves, with the weight of the regularizer being minimized at convergence. We also introduce the use of a Huber loss function in both data fidelity and regularization terms, and present an efficient convex optimization algorithm based on the alternating direction method of multipliers (ADMM) using the equivalent relation between the Huber function and the proximal operator of the one-norm. We illustrate and validate our adaptive Huber-Huber model on synthetic and real images in segmentation, motion estimation, and denoising problems.

Adaptive Regularization in Convex Composite Optimization for Variational Imaging Problems

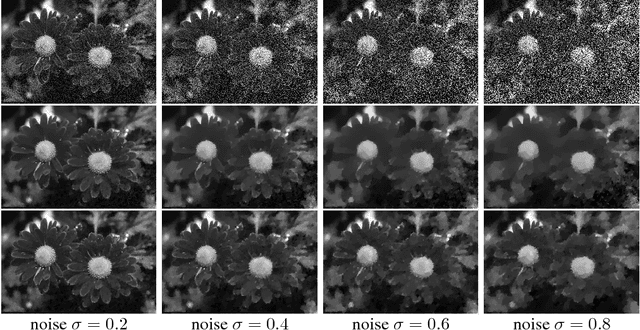
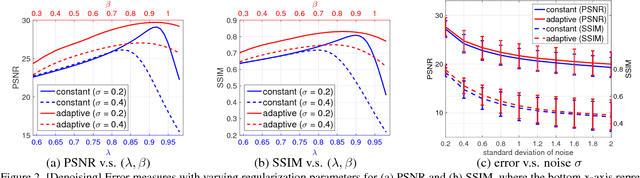
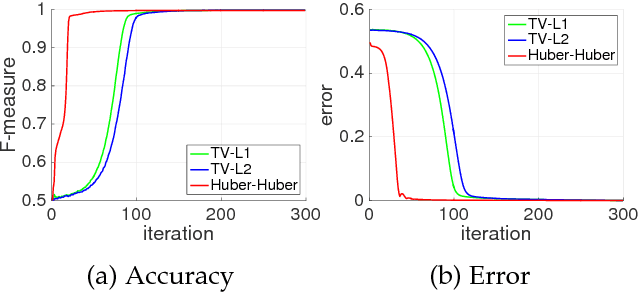
We propose an adaptive regularization scheme in a variational framework where a convex composite energy functional is optimized. We consider a number of imaging problems including denoising, segmentation and motion estimation, which are considered as optimal solutions of the energy functionals that mainly consist of data fidelity, regularization and a control parameter for their trade-off. We presents an algorithm to determine the relative weight between data fidelity and regularization based on the residual that measures how well the observation fits the model. Our adaptive regularization scheme is designed to locally control the regularization at each pixel based on the assumption that the diversity of the residual of a given imaging model spatially varies. The energy optimization is presented in the alternating direction method of multipliers (ADMM) framework where the adaptive regularization is iteratively applied along with mathematical analysis of the proposed algorithm. We demonstrate the robustness and effectiveness of our adaptive regularization through experimental results presenting that the qualitative and quantitative evaluation results of each imaging task are superior to the results with a constant regularization scheme. The desired properties, robustness and effectiveness, of the regularization parameter selection in a variational framework for imaging problems are achieved by merely replacing the static regularization parameter with our adaptive one.

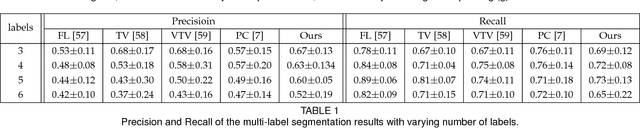
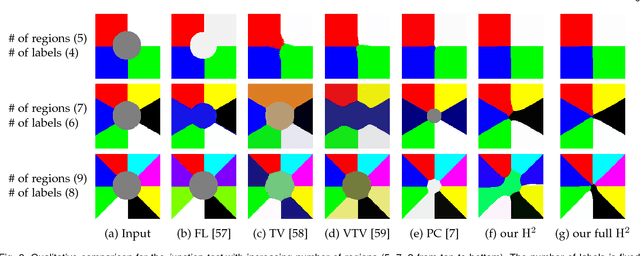
Multi-Label Segmentation via Residual-Driven Adaptive Regularization

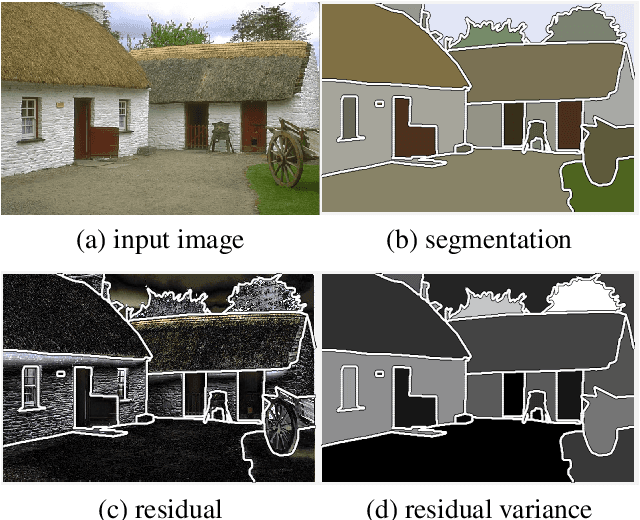
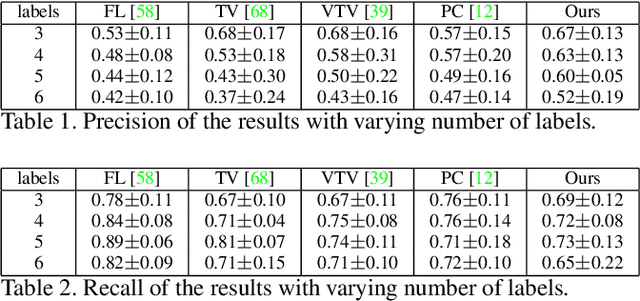
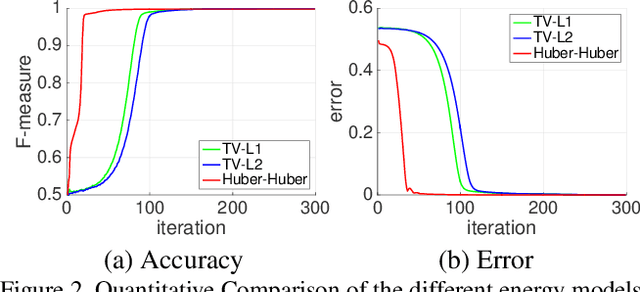
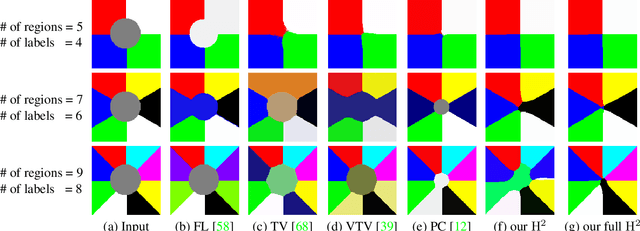
We present a variational multi-label segmentation algorithm based on a robust Huber loss for both the data and the regularizer, minimized within a convex optimization framework. We introduce a novel constraint on the common areas, to bias the solution towards mutually exclusive regions. We also propose a regularization scheme that is adapted to the spatial statistics of the residual at each iteration, resulting in a varying degree of regularization being applied as the algorithm proceeds: the effect of the regularizer is strongest at initialization, and wanes as the solution increasingly fits the data. This minimizes the bias induced by the regularizer at convergence. We design an efficient convex optimization algorithm based on the alternating direction method of multipliers using the equivalent relation between the Huber function and the proximal operator of the one-norm. We empirically validate our proposed algorithm on synthetic and real images and offer an information-theoretic derivation of the cost-function that highlights the modeling choices made.