Revisiting Active Learning under (Human) Label Variation

Access to high-quality labeled data remains a limiting factor in applied supervised learning. While label variation (LV), i.e., differing labels for the same instance, is common, especially in natural language processing, annotation frameworks often still rest on the assumption of a single ground truth. This overlooks human label variation (HLV), the occurrence of plausible differences in annotations, as an informative signal. Similarly, active learning (AL), a popular approach to optimizing the use of limited annotation budgets in training ML models, often relies on at least one of several simplifying assumptions, which rarely hold in practice when acknowledging HLV. In this paper, we examine foundational assumptions about truth and label nature, highlighting the need to decompose observed LV into signal (e.g., HLV) and noise (e.g., annotation error). We survey how the AL and (H)LV communities have addressed -- or neglected -- these distinctions and propose a conceptual framework for incorporating HLV throughout the AL loop, including instance selection, annotator choice, and label representation. We further discuss the integration of large language models (LLM) as annotators. Our work aims to lay a conceptual foundation for HLV-aware active learning, better reflecting the complexities of real-world annotation.

Specialists Outperform Generalists in Ensemble Classification

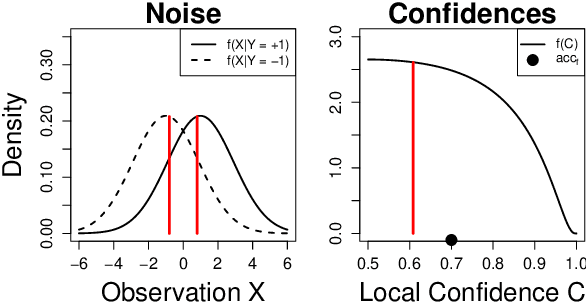
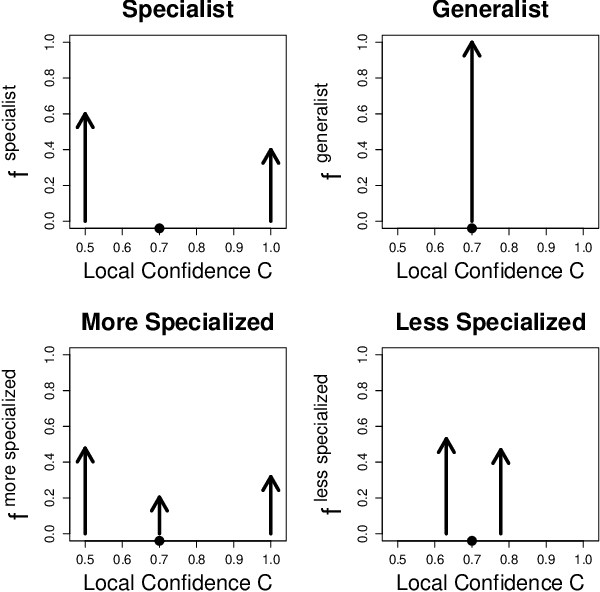
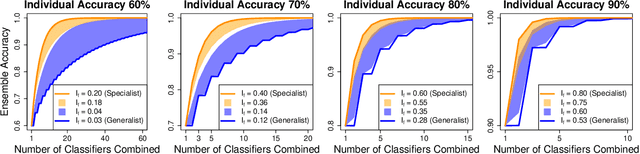
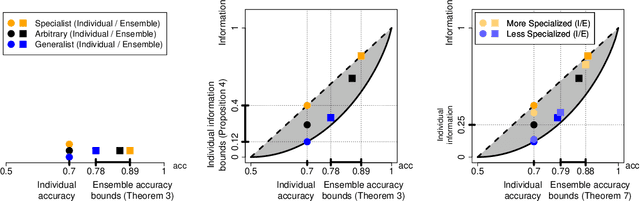
Consider an ensemble of $k$ individual classifiers whose accuracies are known. Upon receiving a test point, each of the classifiers outputs a predicted label and a confidence in its prediction for this particular test point. In this paper, we address the question of whether we can determine the accuracy of the ensemble. Surprisingly, even when classifiers are combined in the statistically optimal way in this setting, the accuracy of the resulting ensemble classifier cannot be computed from the accuracies of the individual classifiers-as would be the case in the standard setting of confidence weighted majority voting. We prove tight upper and lower bounds on the ensemble accuracy. We explicitly construct the individual classifiers that attain the upper and lower bounds: specialists and generalists. Our theoretical results have very practical consequences: (1) If we use ensemble methods and have the choice to construct our individual (independent) classifiers from scratch, then we should aim for specialist classifiers rather than generalists. (2) Our bounds can be used to determine how many classifiers are at least required to achieve a desired ensemble accuracy. Finally, we improve our bounds by considering the mutual information between the true label and the individual classifier's output.