Fault Detection in Solar Thermal Systems using Probabilistic Reconstructions

Solar thermal systems (STS) present a promising avenue for low-carbon heat generation, with a well-running system providing heat at minimal cost and carbon emissions. However, STS can exhibit faults due to improper installation, maintenance, or operation, often resulting in a substantial reduction in efficiency or even damage to the system. As monitoring at the individual level is economically prohibitive for small-scale systems, automated monitoring and fault detection should be used to address such issues. Recent advances in data-driven anomaly detection, particularly in time series analysis, offer a cost-effective solution by leveraging existing sensors to identify abnormal system states. Here, we propose a probabilistic reconstruction-based framework for anomaly detection. We evaluate our method on the publicly available PaSTS dataset of operational domestic STS, which features real-world complexities and diverse fault types. Our experiments show that reconstruction-based methods can detect faults in domestic STS both qualitatively and quantitatively, while generalizing to previously unseen systems. We also demonstrate that our model outperforms both simple and more complex deep learning baselines. Additionally, we show that heteroscedastic uncertainty estimation is essential to fault detection performance. Finally, we discuss the engineering overhead required to unlock these improvements and make a case for simple deep learning models.

Specialists Outperform Generalists in Ensemble Classification

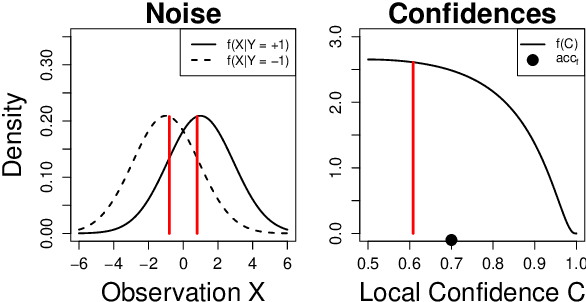
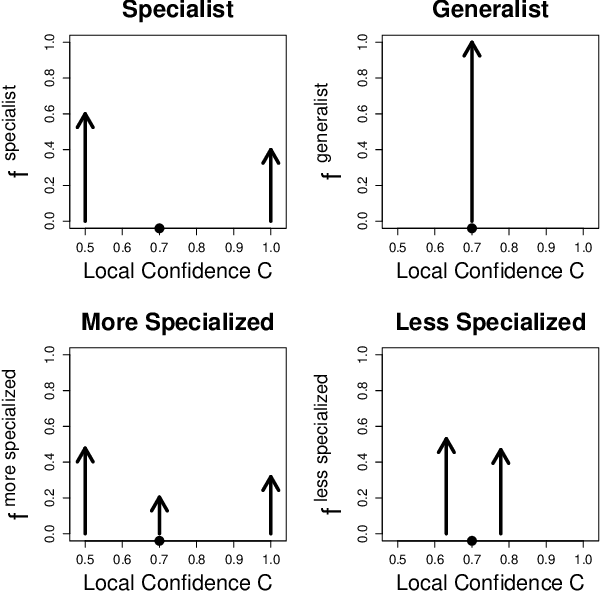
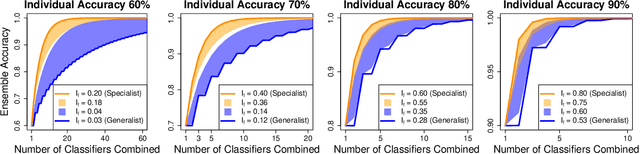
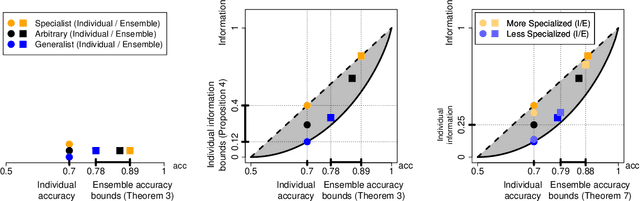
Consider an ensemble of $k$ individual classifiers whose accuracies are known. Upon receiving a test point, each of the classifiers outputs a predicted label and a confidence in its prediction for this particular test point. In this paper, we address the question of whether we can determine the accuracy of the ensemble. Surprisingly, even when classifiers are combined in the statistically optimal way in this setting, the accuracy of the resulting ensemble classifier cannot be computed from the accuracies of the individual classifiers-as would be the case in the standard setting of confidence weighted majority voting. We prove tight upper and lower bounds on the ensemble accuracy. We explicitly construct the individual classifiers that attain the upper and lower bounds: specialists and generalists. Our theoretical results have very practical consequences: (1) If we use ensemble methods and have the choice to construct our individual (independent) classifiers from scratch, then we should aim for specialist classifiers rather than generalists. (2) Our bounds can be used to determine how many classifiers are at least required to achieve a desired ensemble accuracy. Finally, we improve our bounds by considering the mutual information between the true label and the individual classifier's output.