ReLU Network Approximation in Terms of Intrinsic Parameters

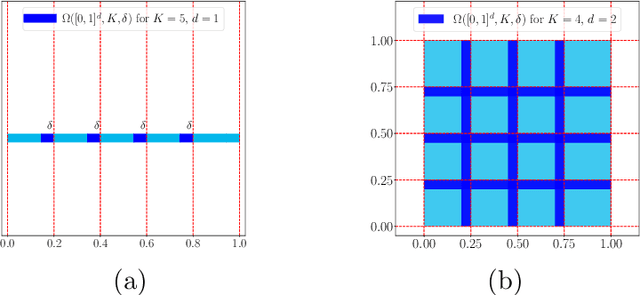
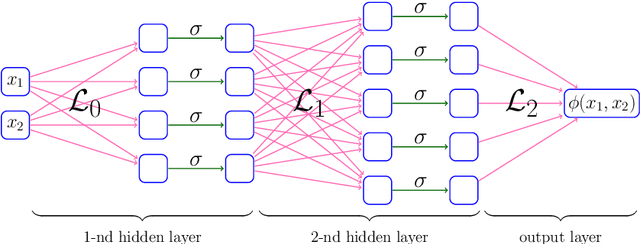
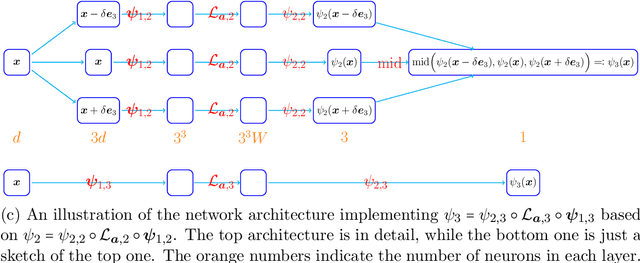
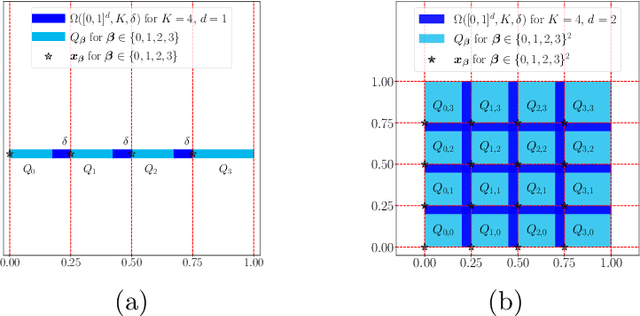
This paper studies the approximation error of ReLU networks in terms of the number of intrinsic parameters (i.e., those depending on the target function $f$). First, we prove by construction that, for any Lipschitz continuous function $f$ on $[0,1]^d$ with a Lipschitz constant $\lambda>0$, a ReLU network with $n+2$ intrinsic parameters can approximate $f$ with an exponentially small error $5\lambda \sqrt{d}\,2^{-n}$ measured in the $L^p$-norm for $p\in [1,\infty)$. More generally for an arbitrary continuous function $f$ on $[0,1]^d$ with a modulus of continuity $\omega_f(\cdot)$, the approximation error is $\omega_f(\sqrt{d}\, 2^{-n})+2^{-n+2}\omega_f(\sqrt{d})$. Next, we extend these two results from the $L^p$-norm to the $L^\infty$-norm at a price of $3^d n+2$ intrinsic parameters. Finally, by using a high-precision binary representation and the bit extraction technique via a fixed ReLU network independent of the target function, we design, theoretically, a ReLU network with only three intrinsic parameters to approximate H\"older continuous functions with an arbitrarily small error.

Stationary Density Estimation of Itô Diffusions Using Deep Learning

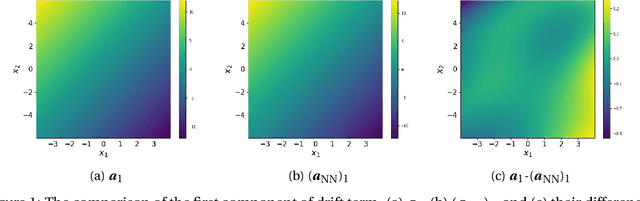
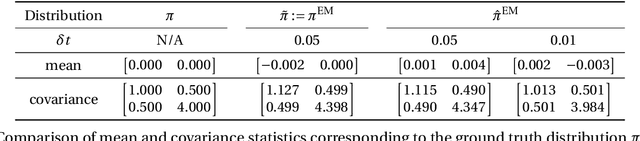
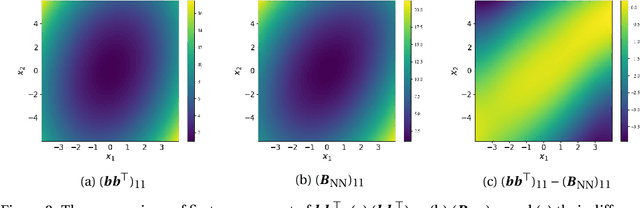
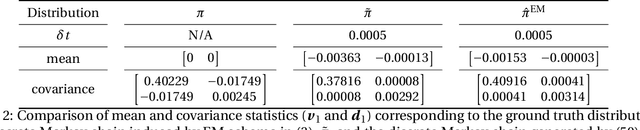
In this paper, we consider the density estimation problem associated with the stationary measure of ergodic It\^o diffusions from a discrete-time series that approximate the solutions of the stochastic differential equations. To take an advantage of the characterization of density function through the stationary solution of a parabolic-type Fokker-Planck PDE, we proceed as follows. First, we employ deep neural networks to approximate the drift and diffusion terms of the SDE by solving appropriate supervised learning tasks. Subsequently, we solve a steady-state Fokker-Plank equation associated with the estimated drift and diffusion coefficients with a neural-network-based least-squares method. We establish the convergence of the proposed scheme under appropriate mathematical assumptions, accounting for the generalization errors induced by regressing the drift and diffusion coefficients, and the PDE solvers. This theoretical study relies on a recent perturbation theory of Markov chain result that shows a linear dependence of the density estimation to the error in estimating the drift term, and generalization error results of nonparametric regression and of PDE regression solution obtained with neural-network models. The effectiveness of this method is reflected by numerical simulations of a two-dimensional Student's t distribution and a 20-dimensional Langevin dynamics.

Blending Pruning Criteria for Convolutional Neural Networks

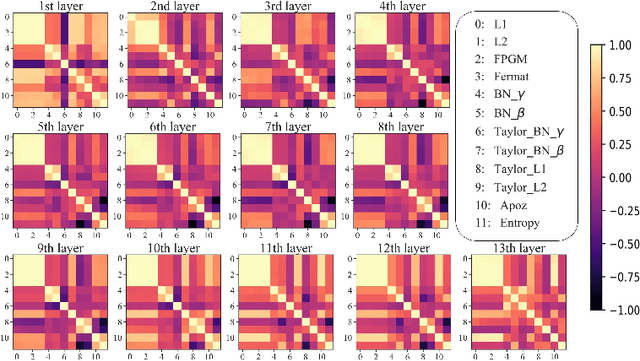
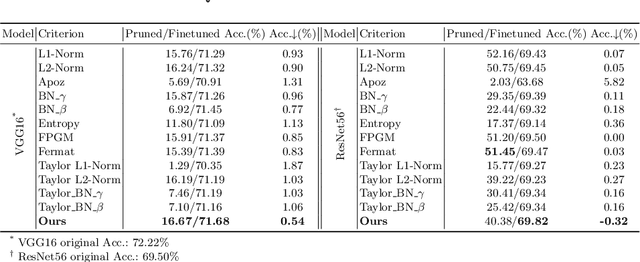
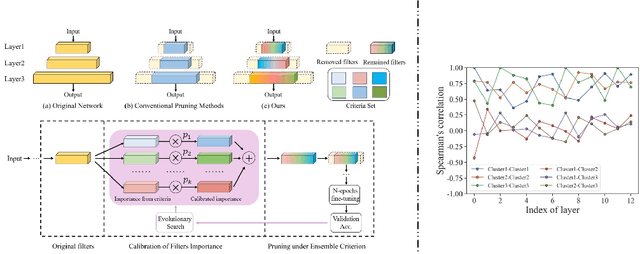
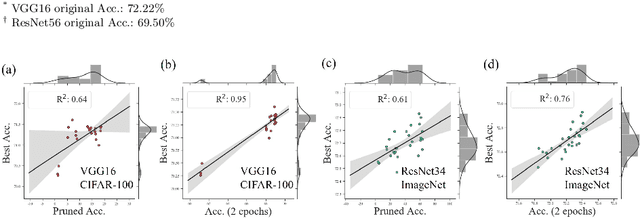
The advancement of convolutional neural networks (CNNs) on various vision applications has attracted lots of attention. Yet the majority of CNNs are unable to satisfy the strict requirement for real-world deployment. To overcome this, the recent popular network pruning is an effective method to reduce the redundancy of the models. However, the ranking of filters according to their "importance" on different pruning criteria may be inconsistent. One filter could be important according to a certain criterion, while it is unnecessary according to another one, which indicates that each criterion is only a partial view of the comprehensive "importance". From this motivation, we propose a novel framework to integrate the existing filter pruning criteria by exploring the criteria diversity. The proposed framework contains two stages: Criteria Clustering and Filters Importance Calibration. First, we condense the pruning criteria via layerwise clustering based on the rank of "importance" score. Second, within each cluster, we propose a calibration factor to adjust their significance for each selected blending candidates and search for the optimal blending criterion via Evolutionary Algorithm. Quantitative results on the CIFAR-100 and ImageNet benchmarks show that our framework outperforms the state-of-the-art baselines, regrading to the compact model performance after pruning.

Deep Network Approximation: Achieving Arbitrary Accuracy with Fixed Number of Neurons

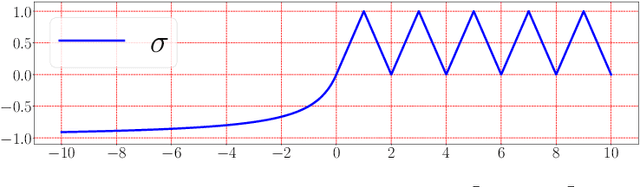
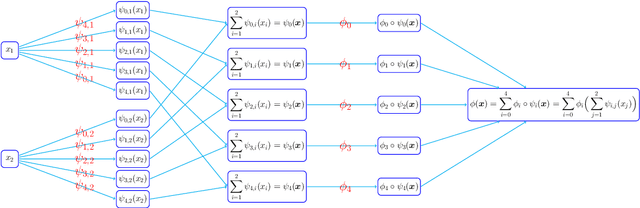
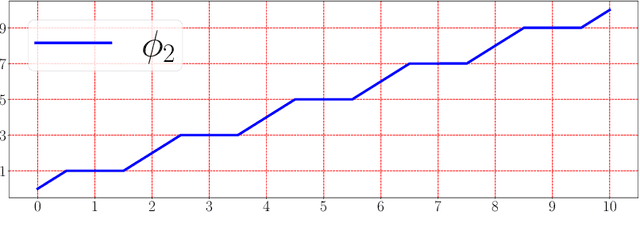
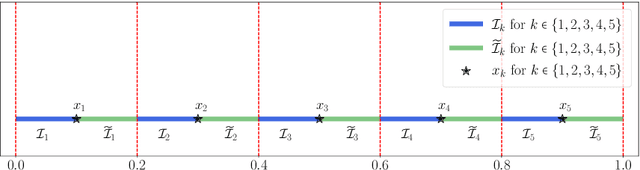
This paper develops simple feed-forward neural networks that achieve the universal approximation property for all continuous functions with a fixed finite number of neurons. These neural networks are simple because they are designed with a simple and computable continuous activation function $\sigma$ leveraging a triangular-wave function and a softsign function. We prove that $\sigma$-activated networks with width $36d(2d+1)$ and depth $11$ can approximate any continuous function on a $d$-dimensioanl hypercube within an arbitrarily small error. Hence, for supervised learning and its related regression problems, the hypothesis space generated by these networks with a size not smaller than $36d(2d+1)\times 11$ is dense in the space of continuous functions. Furthermore, classification functions arising from image and signal classification are in the hypothesis space generated by $\sigma$-activated networks with width $36d(2d+1)$ and depth $12$, when there exist pairwise disjoint closed bounded subsets of $\mathbb{R}^d$ such that the samples of the same class are located in the same subset.

Solving PDEs on Unknown Manifolds with Machine Learning

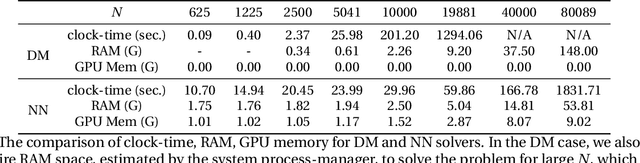
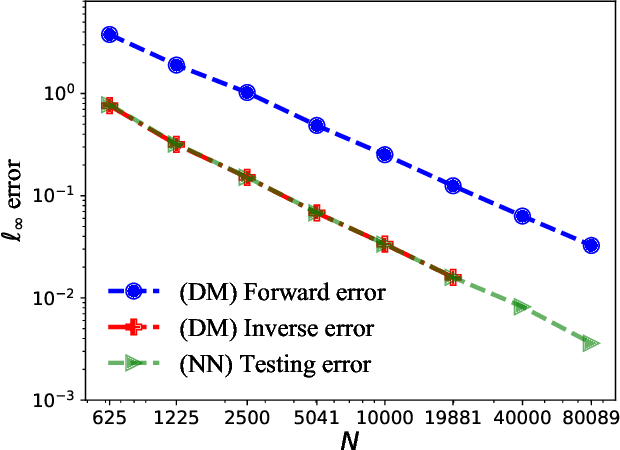
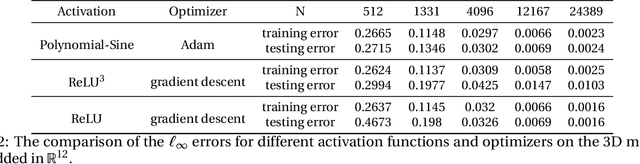
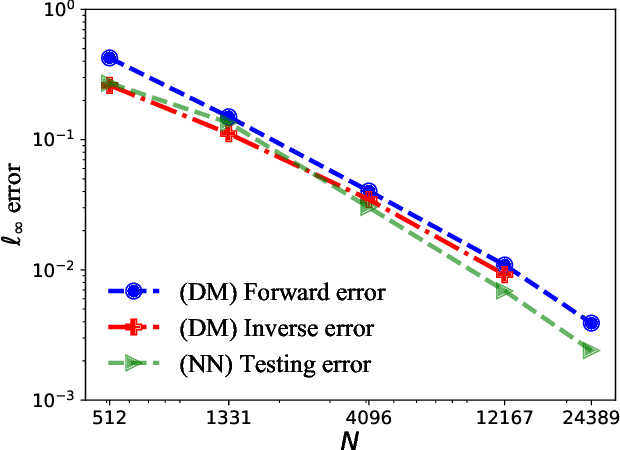
This paper proposes a mesh-free computational framework and machine learning theory for solving elliptic PDEs on unknown manifolds, identified with point clouds, based on diffusion maps (DM) and deep learning. The PDE solver is formulated as a supervised learning task to solve a least-squares regression problem that imposes an algebraic equation approximating a PDE (and boundary conditions if applicable). This algebraic equation involves a graph-Laplacian type matrix obtained via DM asymptotic expansion, which is a consistent estimator of second-order elliptic differential operators. The resulting numerical method is to solve a highly non-convex empirical risk minimization problem subjected to a solution from a hypothesis space of neural-network type functions. In a well-posed elliptic PDE setting, when the hypothesis space consists of feedforward neural networks with either infinite width or depth, we show that the global minimizer of the empirical loss function is a consistent solution in the limit of large training data. When the hypothesis space is a two-layer neural network, we show that for a sufficiently large width, the gradient descent method can identify a global minimizer of the empirical loss function. Supporting numerical examples demonstrate the convergence of the solutions and the effectiveness of the proposed solver in avoiding numerical issues that hampers the traditional approach when a large data set becomes available, e.g., large matrix inversion.

The Discovery of Dynamics via Linear Multistep Methods and Deep Learning: Error Estimation

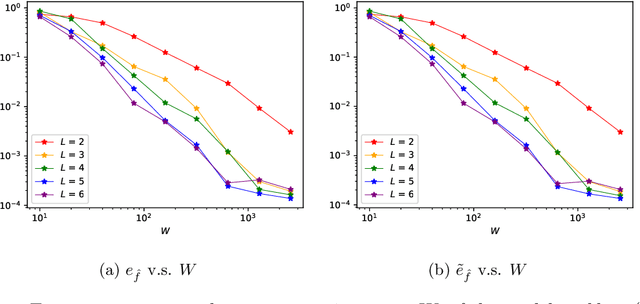
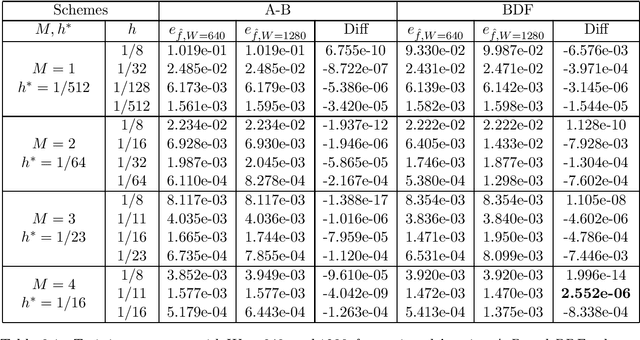
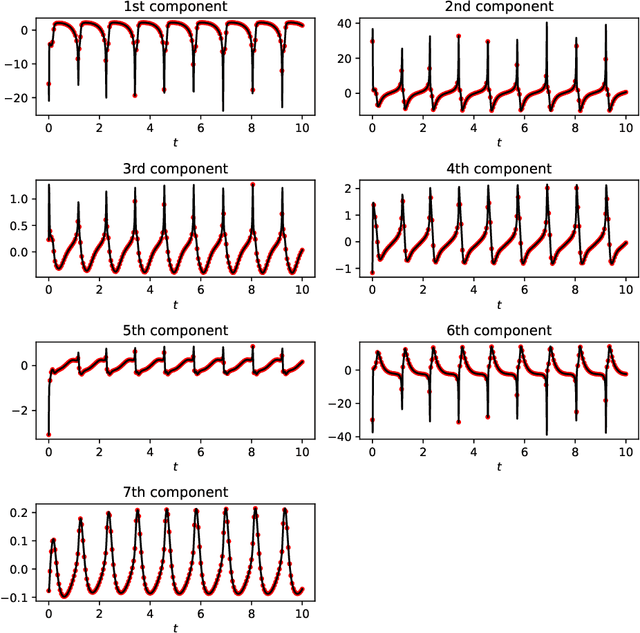
Identifying hidden dynamics from observed data is a significant and challenging task in a wide range of applications. Recently, the combination of linear multistep methods (LMMs) and deep learning has been successfully employed to discover dynamics, whereas a complete convergence analysis of this approach is still under development. In this work, we consider the deep network-based LMMs for the discovery of dynamics. We put forward error estimates for these methods using the approximation property of deep networks. It indicates, for certain families of LMMs, that the $\ell^2$ grid error is bounded by the sum of $O(h^p)$ and the network approximation error, where $h$ is the time step size and $p$ is the local truncation error order. Numerical results of several physically relevant examples are provided to demonstrate our theory.

Optimal Approximation Rate of ReLU Networks in terms of Width and Depth

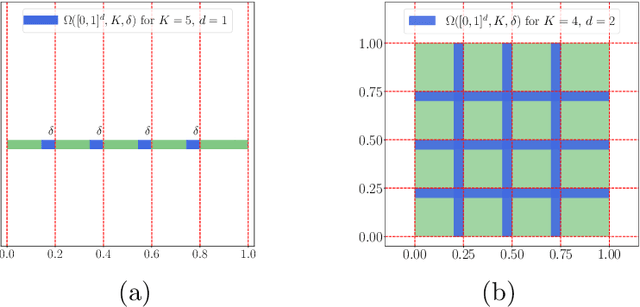
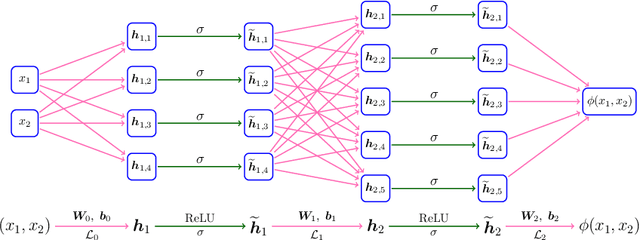
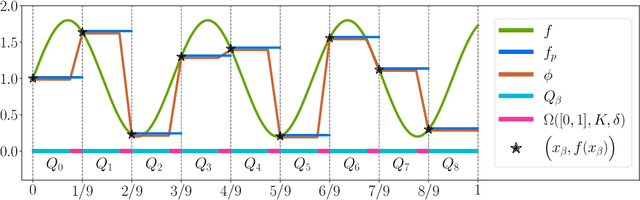
This paper concentrates on the approximation power of deep feed-forward neural networks in terms of width and depth. It is proved by construction that ReLU networks with width $\mathcal{O}\big(\max\{d\lfloor N^{1/d}\rfloor,\, N+2\}\big)$ and depth $\mathcal{O}(L)$ can approximate a H\"older continuous function on $[0,1]^d$ with an approximation rate $\mathcal{O}\big(\lambda\sqrt{d} (N^2L^2\ln N)^{-\alpha/d}\big)$, where $\alpha\in (0,1]$ and $\lambda>0$ are H\"older order and constant, respectively. Such a rate is optimal up to a constant in terms of width and depth separately, while existing results are only nearly optimal without the logarithmic factor in the approximation rate. More generally, for an arbitrary continuous function $f$ on $[0,1]^d$, the approximation rate becomes $\mathcal{O}\big(\,\sqrt{d}\,\omega_f\big( (N^2L^2\ln N)^{-1/d}\big)\,\big)$, where $\omega_f(\cdot)$ is the modulus of continuity. We also extend our analysis to any continuous function $f$ on a bounded set. Particularly, if ReLU networks with depth $31$ and width $\mathcal{O}(N)$ are used to approximate one-dimensional Lipschitz continuous functions on $[0,1]$ with a Lipschitz constant $\lambda>0$, the approximation rate in terms of the total number of parameters, $W=\mathcal{O}(N^2)$, becomes $\mathcal{O}(\tfrac{\lambda}{W\ln W})$, which has not been discovered in the literature for fixed-depth ReLU networks.

Friedrichs Learning: Weak Solutions of Partial Differential Equations via Deep Learning

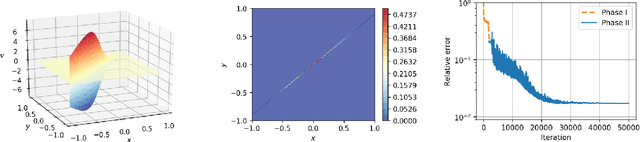
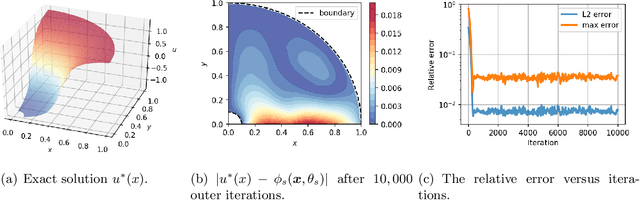
This paper proposes Friedrichs learning as a novel deep learning methodology that can learn the weak solutions of PDEs via a minmax formulation, which transforms the PDE problem into a minimax optimization problem to identify weak solutions. The name "Friedrichs learning" is for highlighting the close relationship between our learning strategy and Friedrichs theory on symmetric systems of PDEs. The weak solution and the test function in the weak formulation are parameterized as deep neural networks in a mesh-free manner, which are alternately updated to approach the optimal solution networks approximating the weak solution and the optimal test function, respectively. Extensive numerical results indicate that our mesh-free method can provide reasonably good solutions to a wide range of PDEs defined on regular and irregular domains in various dimensions, where classical numerical methods such as finite difference methods and finite element methods may be tedious or difficult to be applied.

Reproducing Activation Function for Deep Learning

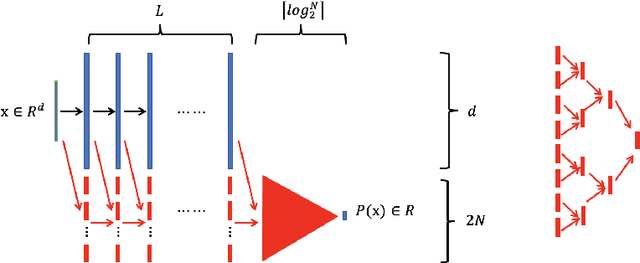
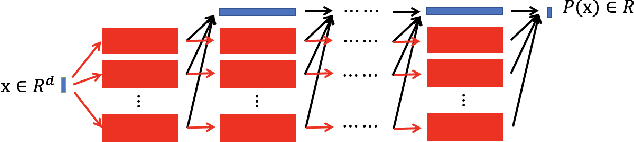
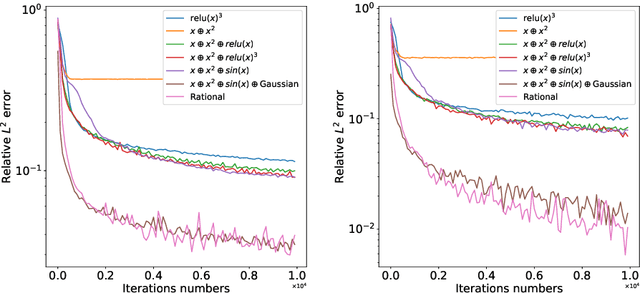
In this paper, we propose the reproducing activation function to improve deep learning accuracy for various applications ranging from computer vision problems to scientific computing problems. The idea of reproducing activation functions is to employ several basic functions and their learnable linear combination to construct neuron-wise data-driven activation functions for each neuron. Armed with such activation functions, deep neural networks can reproduce traditional approximation tools and, therefore, approximate target functions with a smaller number of parameters than traditional neural networks. In terms of training dynamics of deep learning, reproducing activation functions can generate neural tangent kernels with a better condition number than traditional activation functions lessening the spectral bias of deep learning. As demonstrated by extensive numerical tests, the proposed activation function can facilitate the convergence of deep learning optimization for a solution with higher accuracy than existing deep learning solvers for audio/image/video reconstruction, PDEs, and eigenvalue problems.

Efficient Attention Network: Accelerate Attention by Searching Where to Plug

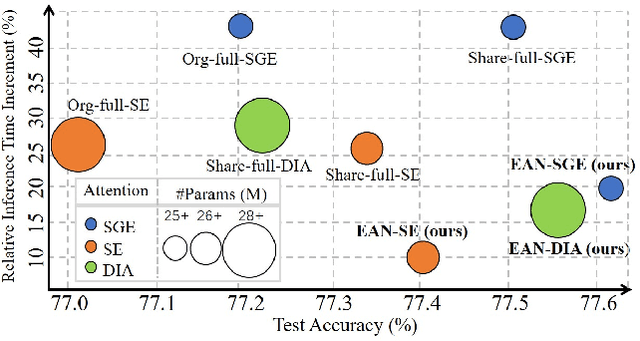
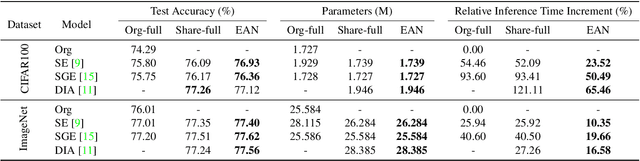
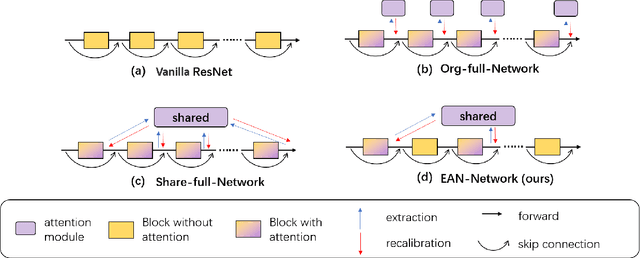
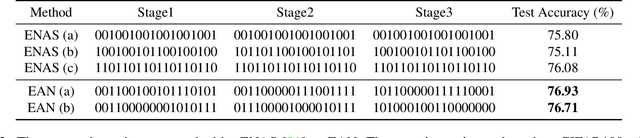
Recently, many plug-and-play self-attention modules are proposed to enhance the model generalization by exploiting the internal information of deep convolutional neural networks (CNNs). Previous works lay an emphasis on the design of attention module for specific functionality, e.g., light-weighted or task-oriented attention. However, they ignore the importance of where to plug in the attention module since they connect the modules individually with each block of the entire CNN backbone for granted, leading to incremental computational cost and number of parameters with the growth of network depth. Thus, we propose a framework called Efficient Attention Network (EAN) to improve the efficiency for the existing attention modules. In EAN, we leverage the sharing mechanism (Huang et al. 2020) to share the attention module within the backbone and search where to connect the shared attention module via reinforcement learning. Finally, we obtain the attention network with sparse connections between the backbone and modules, while (1) maintaining accuracy (2) reducing extra parameter increment and (3) accelerating inference. Extensive experiments on widely-used benchmarks and popular attention networks show the effectiveness of EAN. Furthermore, we empirically illustrate that our EAN has the capacity of transferring to other tasks and capturing the informative features. The code is available at https://github.com/gbup-group/EAN-efficient-attention-network