DP-DCAN: Differentially Private Deep Contrastive Autoencoder Network for Single-cell Clustering

Single-cell RNA sequencing (scRNA-seq) is important to transcriptomic analysis of gene expression. Recently, deep learning has facilitated the analysis of high-dimensional single-cell data. Unfortunately, deep learning models may leak sensitive information about users. As a result, Differential Privacy (DP) is increasingly used to protect privacy. However, existing DP methods usually perturb whole neural networks to achieve differential privacy, and hence result in great performance overheads. To address this challenge, in this paper, we take advantage of the uniqueness of the autoencoder that it outputs only the dimension-reduced vector in the middle of the network, and design a Differentially Private Deep Contrastive Autoencoder Network (DP-DCAN) by partial network perturbation for single-cell clustering. Since only partial network is added with noise, the performance improvement is obvious and twofold: one part of network is trained with less noise due to a bigger privacy budget, and the other part is trained without any noise. Experimental results of six datasets have verified that DP-DCAN is superior to the traditional DP scheme with whole network perturbation. Moreover, DP-DCAN demonstrates strong robustness to adversarial attacks. The code is available at https://github.com/LFD-byte/DP-DCAN.

Robust Motion Averaging for Multi-view Registration of Point Sets Based Maximum Correntropy Criterion

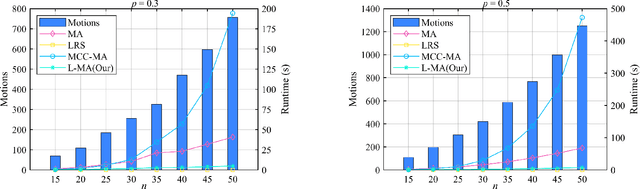
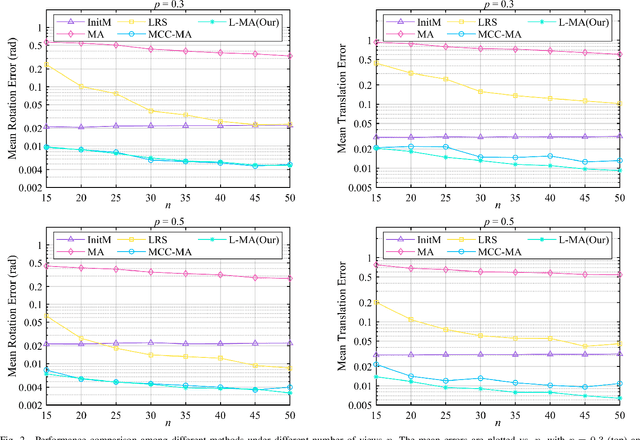
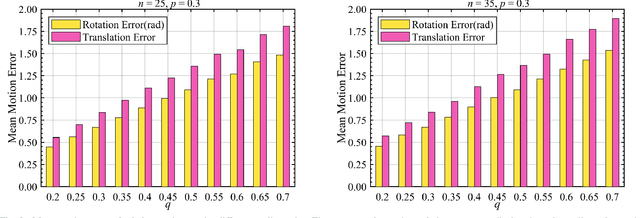
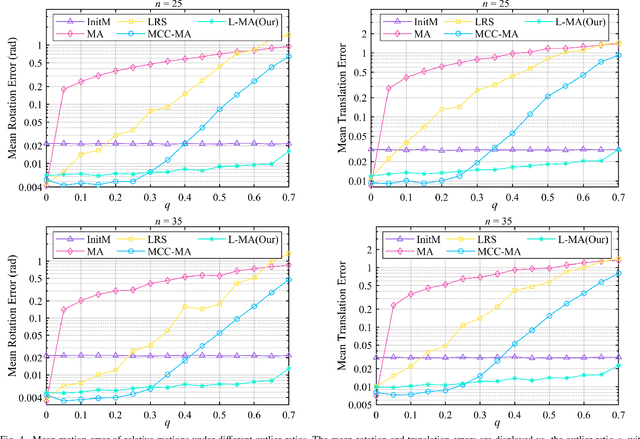
As an efficient algorithm to solve the multi-view registration problem,the motion averaging (MA) algorithm has been extensively studied and many MA-based algorithms have been introduced. They aim at recovering global motions from relative motions and exploiting information redundancy to average accumulative errors. However, one property of these methods is that they use Guass-Newton method to solve a least squares problem for the increment of global motions, which may lead to low efficiency and poor robustness to outliers. In this paper, we propose a novel motion averaging framework for the multi-view registration with Laplacian kernel-based maximum correntropy criterion (LMCC). Utilizing the Lie algebra motion framework and the correntropy measure, we propose a new cost function that takes all constraints supplied by relative motions into account. Obtaining the increment used to correct the global motions, can further be formulated as an optimization problem aimed at maximizing the cost function. By virtue of the quadratic technique, the optimization problem can be solved by dividing into two subproblems, i.e., computing the weight for each relative motion according to the current residuals and solving a second-order cone program problem (SOCP) for the increment in the next iteration. We also provide a novel strategy for determining the kernel width which ensures that our method can efficiently exploit information redundancy supplied by relative motions in the presence of many outliers. Finally, we compare the proposed method with other MA-based multi-view registration methods to verify its performance. Experimental tests on synthetic and real data demonstrate that our method achieves superior performance in terms of efficiency, accuracy and robustness.

Learning Multi-Task Gaussian Process Over Heterogeneous Input Domains

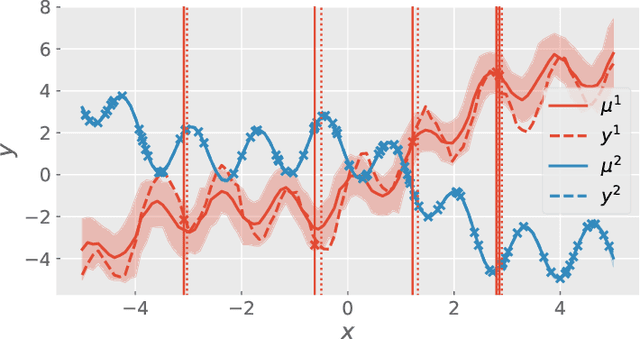
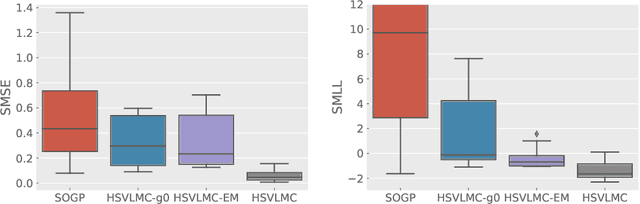
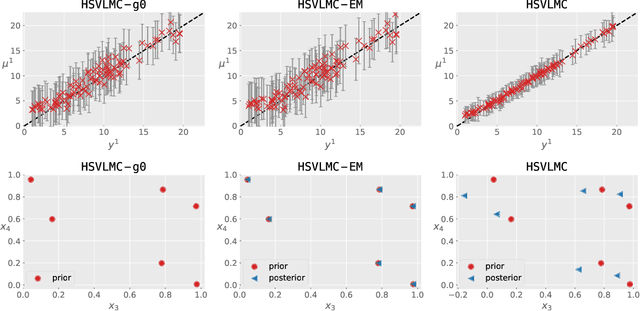
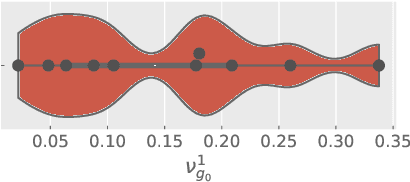
Multi-task Gaussian process (MTGP) is a well-known non-parametric Bayesian model for learning correlated tasks effectively by transferring knowledge across tasks. But current MTGP models are usually limited to the multi-task scenario defined in the same input domain, leaving no space for tackling the practical heterogeneous case, i.e., the features of input domains vary over tasks. To this end, this paper presents a novel heterogeneous stochastic variational linear model of coregionalization (HSVLMC) model for simultaneously learning the tasks with varied input domains. Particularly, we develop the stochastic variational framework with a Bayesian calibration method that (i) takes into account the effect of dimensionality reduction raised by domain mapping in order to achieve effective input alignment; and (ii) employs a residual modeling strategy to leverage the inductive bias brought by prior domain mappings for better model inference. Finally, the superiority of the proposed model against existing LMC models has been extensively verified on diverse heterogeneous multi-task cases.

Scalable Multi-Task Gaussian Processes with Neural Embedding of Coregionalization

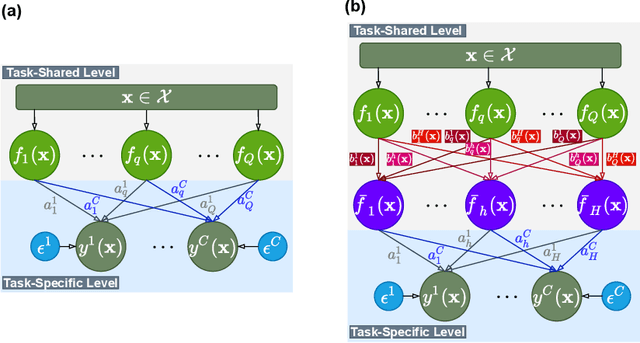
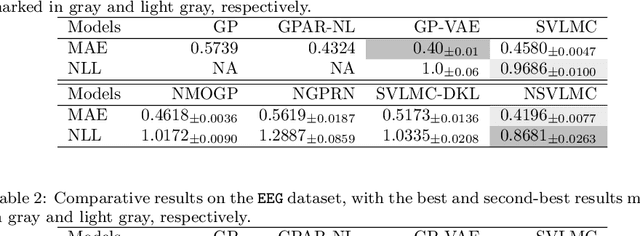
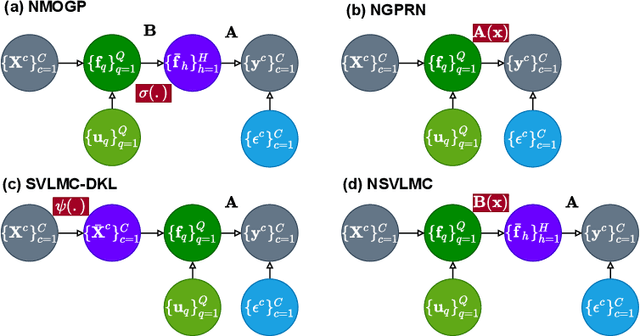
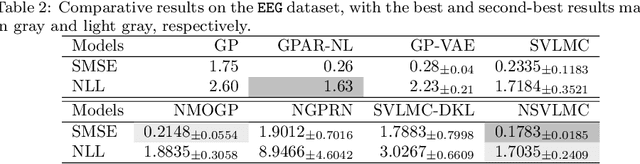
Multi-task regression attempts to exploit the task similarity in order to achieve knowledge transfer across related tasks for performance improvement. The application of Gaussian process (GP) in this scenario yields the non-parametric yet informative Bayesian multi-task regression paradigm. Multi-task GP (MTGP) provides not only the prediction mean but also the associated prediction variance to quantify uncertainty, thus gaining popularity in various scenarios. The linear model of coregionalization (LMC) is a well-known MTGP paradigm which exploits the dependency of tasks through linear combination of several independent and diverse GPs. The LMC however suffers from high model complexity and limited model capability when handling complicated multi-task cases. To this end, we develop the neural embedding of coregionalization that transforms the latent GPs into a high-dimensional latent space to induce rich yet diverse behaviors. Furthermore, we use advanced variational inference as well as sparse approximation to devise a tight and compact evidence lower bound (ELBO) for higher quality of scalable model inference. Extensive numerical experiments have been conducted to verify the higher prediction quality and better generalization of our model, named NSVLMC, on various real-world multi-task datasets and the cross-fluid modeling of unsteady fluidized bed.

Deep Probabilistic Time Series Forecasting using Augmented Recurrent Input for Dynamic Systems

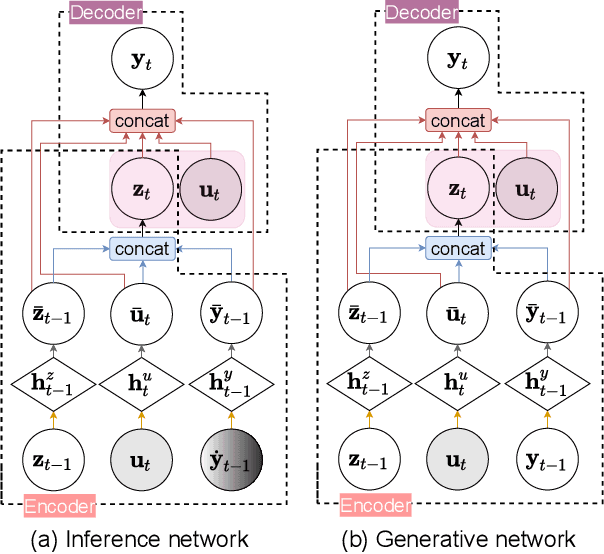
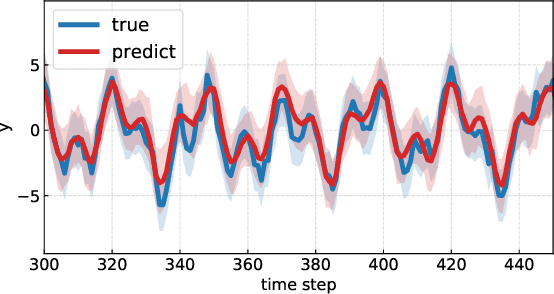
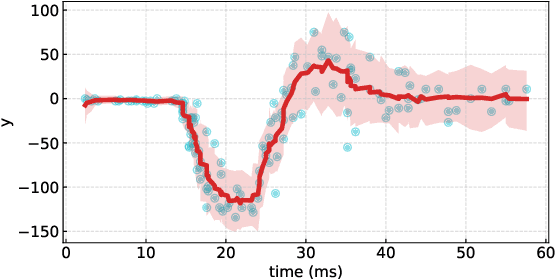
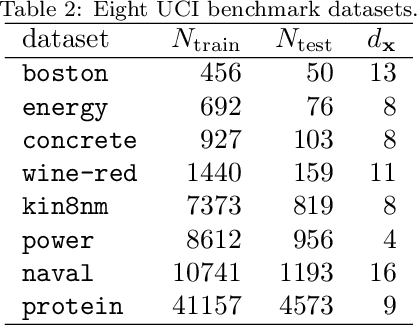
The demand of probabilistic time series forecasting has been recently raised in various dynamic system scenarios, for example, system identification and prognostic and health management of machines. To this end, we combine the advances in both deep generative models and state space model (SSM) to come up with a novel, data-driven deep probabilistic sequence model. Specially, we follow the popular encoder-decoder generative structure to build the recurrent neural networks (RNN) assisted variational sequence model on an augmented recurrent input space, which could induce rich stochastic sequence dependency. Besides, in order to alleviate the issue of inconsistency between training and predicting as well as improving the mining of dynamic patterns, we (i) propose using a hybrid output as input at next time step, which brings training and predicting into alignment; and (ii) further devise a generalized auto-regressive strategy that encodes all the historical dependencies at current time step. Thereafter, we first investigate the methodological characteristics of the proposed deep probabilistic sequence model on toy cases, and then comprehensively demonstrate the superiority of our model against existing deep probabilistic SSM models through extensive numerical experiments on eight system identification benchmarks from various dynamic systems. Finally, we apply our sequence model to a real-world centrifugal compressor sensor data forecasting problem, and again verify its outstanding performance by quantifying the time series predictive distribution.

Statistical patterns of word frequency suggesting the probabilistic nature of human languages

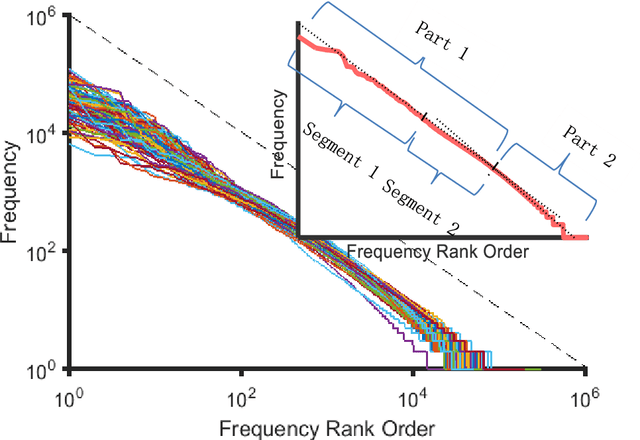
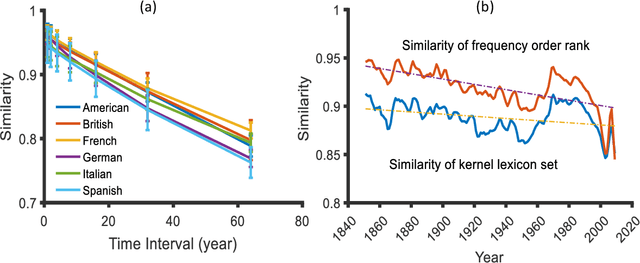
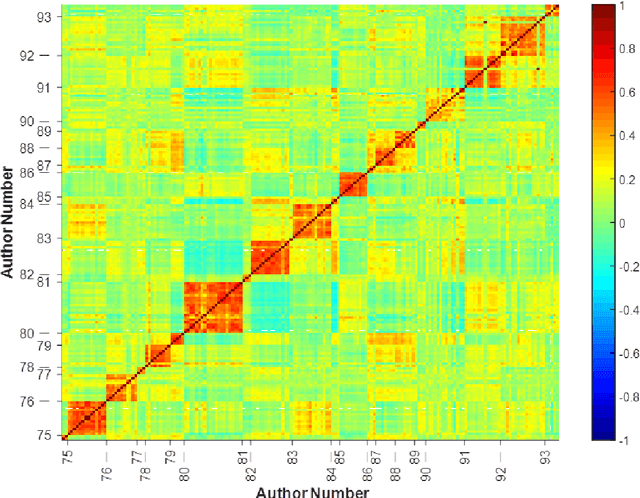
Traditional linguistic theories have largely regard language as a formal system composed of rigid rules. However, their failures in processing real language, the recent successes in statistical natural language processing, and the findings of many psychological experiments have suggested that language may be more a probabilistic system than a formal system, and thus cannot be faithfully modeled with the either/or rules of formal linguistic theory. The present study, based on authentic language data, confirmed that those important linguistic issues, such as linguistic universal, diachronic drift, and language variations can be translated into probability and frequency patterns in parole. These findings suggest that human language may well be probabilistic systems by nature, and that statistical may well make inherent properties of human languages.

Modulating Scalable Gaussian Processes for Expressive Statistical Learning

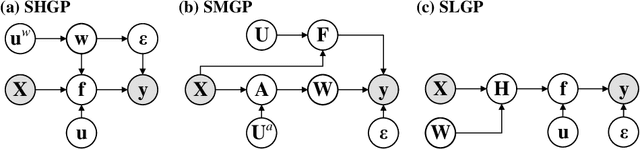
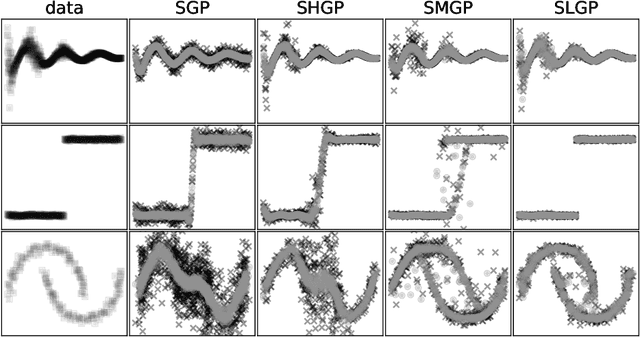
For a learning task, Gaussian process (GP) is interested in learning the statistical relationship between inputs and outputs, since it offers not only the prediction mean but also the associated variability. The vanilla GP however struggles to learn complicated distribution with the property of, e.g., heteroscedastic noise, multi-modality and non-stationarity, from massive data due to the Gaussian marginal and the cubic complexity. To this end, this article studies new scalable GP paradigms including the non-stationary heteroscedastic GP, the mixture of GPs and the latent GP, which introduce additional latent variables to modulate the outputs or inputs in order to learn richer, non-Gaussian statistical representation. We further resort to different variational inference strategies to arrive at analytical or tighter evidence lower bounds (ELBOs) of the marginal likelihood for efficient and effective model training. Extensive numerical experiments against state-of-the-art GP and neural network (NN) counterparts on various tasks verify the superiority of these scalable modulated GPs, especially the scalable latent GP, for learning diverse data distributions.

Deep Latent-Variable Kernel Learning

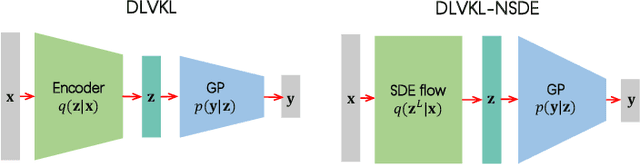
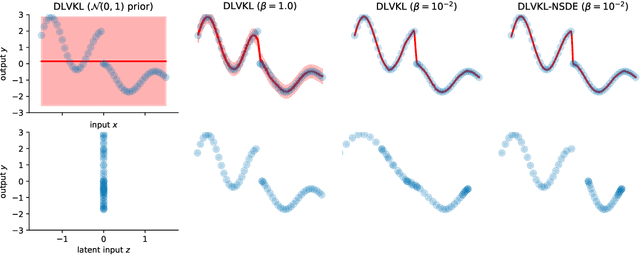
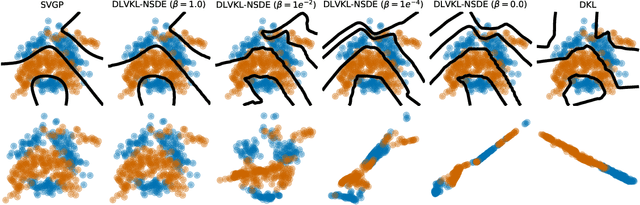
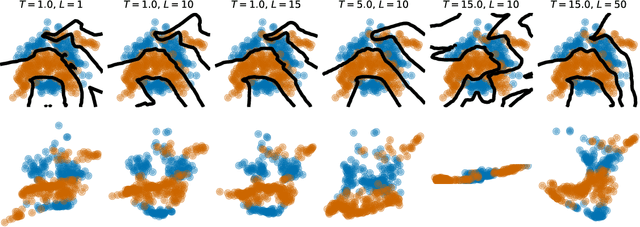
Deep kernel learning (DKL) leverages the connection between Gaussian process (GP) and neural networks (NN) to build an end-to-end, hybrid model. It combines the capability of NN to learn rich representations under massive data and the non-parametric property of GP to achieve automatic calibration. However, the deterministic encoder may weaken the model calibration of the following GP part, especially on small datasets, due to the free latent representation. We therefore present a complete deep latent-variable kernel learning (DLVKL) model wherein the latent variables perform stochastic encoding for regularized representation. Theoretical analysis however indicates that the DLVKL with i.i.d. prior for latent variables suffers from posterior collapse and degenerates to a constant predictor. Hence, we further enhance the DLVKL from two aspects: (i) the complicated variational posterior through neural stochastic differential equation (NSDE) to reduce the divergence gap, and (ii) the hybrid prior taking knowledge from both the SDE prior and the posterior to arrive at a flexible trade-off. Intensive experiments imply that the DLVKL-NSDE performs similarly to the well calibrated GP on small datasets, and outperforms existing deep GPs on large datasets.

Scalable Gaussian Process Classification with Additive Noise for Various Likelihoods

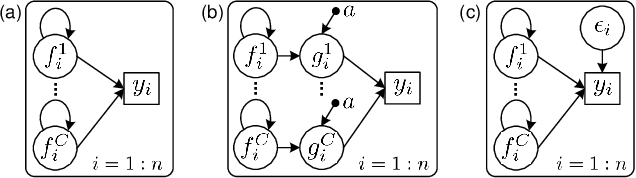
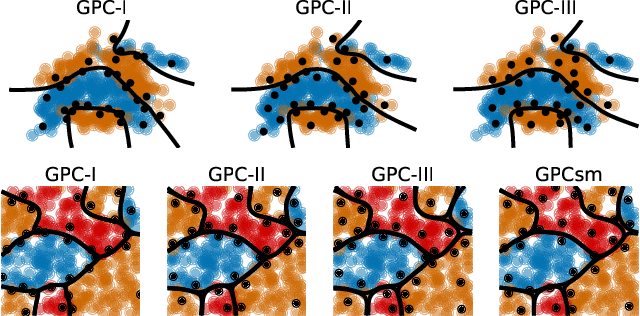
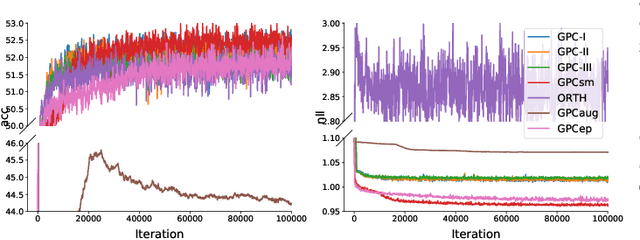
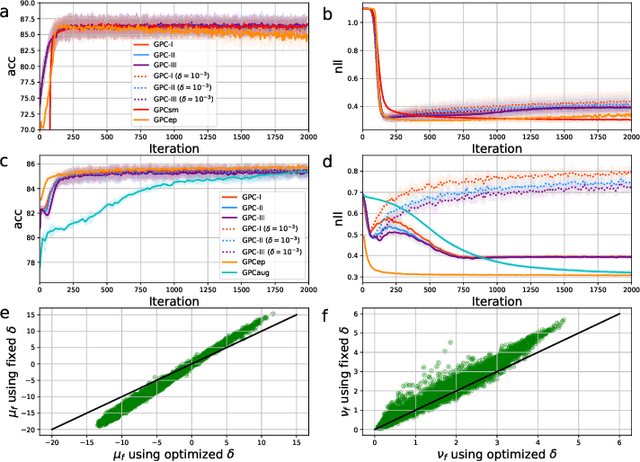
Gaussian process classification (GPC) provides a flexible and powerful statistical framework describing joint distributions over function space. Conventional GPCs however suffer from (i) poor scalability for big data due to the full kernel matrix, and (ii) intractable inference due to the non-Gaussian likelihoods. Hence, various scalable GPCs have been proposed through (i) the sparse approximation built upon a small inducing set to reduce the time complexity; and (ii) the approximate inference to derive analytical evidence lower bound (ELBO). However, these scalable GPCs equipped with analytical ELBO are limited to specific likelihoods or additional assumptions. In this work, we present a unifying framework which accommodates scalable GPCs using various likelihoods. Analogous to GP regression (GPR), we introduce additive noises to augment the probability space for (i) the GPCs with step, (multinomial) probit and logit likelihoods via the internal variables; and particularly, (ii) the GPC using softmax likelihood via the noise variables themselves. This leads to unified scalable GPCs with analytical ELBO by using variational inference. Empirically, our GPCs showcase better results than state-of-the-art scalable GPCs for extensive binary/multi-class classification tasks with up to two million data points.

Anomaly Detection via Graphical Lasso

Anomalies and outliers are common in real-world data, and they can arise from many sources, such as sensor faults. Accordingly, anomaly detection is important both for analyzing the anomalies themselves and for cleaning the data for further analysis of its ambient structure. Nonetheless, a precise definition of anomalies is important for automated detection and herein we approach such problems from the perspective of detecting sparse latent effects embedded in large collections of noisy data. Standard Graphical Lasso-based techniques can identify the conditional dependency structure of a collection of random variables based on their sample covariance matrix. However, classic Graphical Lasso is sensitive to outliers in the sample covariance matrix. In particular, several outliers in a sample covariance matrix can destroy the sparsity of its inverse. Accordingly, we propose a novel optimization problem that is similar in spirit to Robust Principal Component Analysis (RPCA) and splits the sample covariance matrix $M$ into two parts, $M=F+S$, where $F$ is the cleaned sample covariance whose inverse is sparse and computable by Graphical Lasso, and $S$ contains the outliers in $M$. We accomplish this decomposition by adding an additional $ \ell_1$ penalty to classic Graphical Lasso, and name it "Robust Graphical Lasso (Rglasso)". Moreover, we propose an Alternating Direction Method of Multipliers (ADMM) solution to the optimization problem which scales to large numbers of unknowns. We evaluate our algorithm on both real and synthetic datasets, obtaining interpretable results and outperforming the standard robust Minimum Covariance Determinant (MCD) method and Robust Principal Component Analysis (RPCA) regarding both accuracy and speed.