Improving Coverage in Combined Prediction Sets with Weighted p-values

Conformal prediction quantifies the uncertainty of machine learning models by augmenting point predictions with valid prediction sets, assuming exchangeability. For complex scenarios involving multiple trials, models, or data sources, conformal prediction sets can be aggregated to create a prediction set that captures the overall uncertainty, often improving precision. However, aggregating multiple prediction sets with individual $1-\alpha$ coverage inevitably weakens the overall guarantee, typically resulting in $1-2\alpha$ worst-case coverage. In this work, we propose a framework for the weighted aggregation of prediction sets, where weights are assigned to each prediction set based on their contribution. Our framework offers flexible control over how the sets are aggregated, achieving tighter coverage bounds that interpolate between the $1-2\alpha$ guarantee of the combined models and the $1-\alpha$ guarantee of an individual model depending on the distribution of weights. We extend our framework to data-dependent weights, and we derive a general procedure for data-dependent weight aggregation that maintains finite-sample validity. We demonstrate the effectiveness of our methods through experiments on synthetic and real data in the mixture-of-experts setting, and we show that aggregation with data-dependent weights provides a form of adaptive coverage.

Weighted Risk Invariance: Domain Generalization under Invariant Feature Shift

Learning models whose predictions are invariant under multiple environments is a promising approach for out-of-distribution generalization. Such models are trained to extract features $X_{\text{inv}}$ where the conditional distribution $Y \mid X_{\text{inv}}$ of the label given the extracted features does not change across environments. Invariant models are also supposed to generalize to shifts in the marginal distribution $p(X_{\text{inv}})$ of the extracted features $X_{\text{inv}}$, a type of shift we call an $\textit{invariant covariate shift}$. However, we show that proposed methods for learning invariant models underperform under invariant covariate shift, either failing to learn invariant models$\unicode{x2014}$even for data generated from simple and well-studied linear-Gaussian models$\unicode{x2014}$or having poor finite-sample performance. To alleviate these problems, we propose $\textit{weighted risk invariance}$ (WRI). Our framework is based on imposing invariance of the loss across environments subject to appropriate reweightings of the training examples. We show that WRI provably learns invariant models, i.e. discards spurious correlations, in linear-Gaussian settings. We propose a practical algorithm to implement WRI by learning the density $p(X_{\text{inv}})$ and the model parameters simultaneously, and we demonstrate empirically that WRI outperforms previous invariant learning methods under invariant covariate shift.

XraySyn: Realistic View Synthesis From a Single Radiograph Through CT Priors

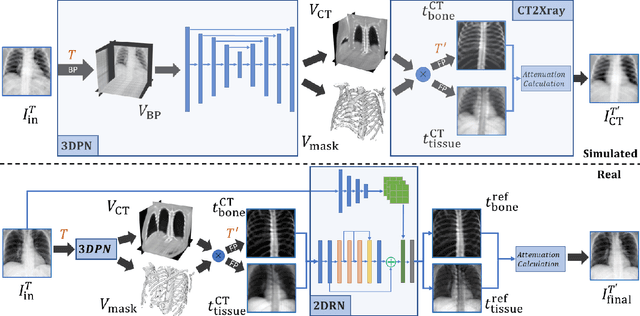
A radiograph visualizes the internal anatomy of a patient through the use of X-ray, which projects 3D information onto a 2D plane. Hence, radiograph analysis naturally requires physicians to relate the prior about 3D human anatomy to 2D radiographs. Synthesizing novel radiographic views in a small range can assist physicians in interpreting anatomy more reliably; however, radiograph view synthesis is heavily ill-posed, lacking in paired data, and lacking in differentiable operations to leverage learning-based approaches. To address these problems, we use Computed Tomography (CT) for radiograph simulation and design a differentiable projection algorithm, which enables us to achieve geometrically consistent transformations between the radiography and CT domains. Our method, XraySyn, can synthesize novel views on real radiographs through a combination of realistic simulation and finetuning on real radiographs. To the best of our knowledge, this is the first work on radiograph view synthesis. We show that by gaining an understanding of radiography in 3D space, our method can be applied to radiograph bone extraction and suppression without groundtruth bone labels.