Conformal Policy Control

An agent must try new behaviors to explore and improve. In high-stakes environments, an agent that violates safety constraints may cause harm and must be taken offline, curtailing any future interaction. Imitating old behavior is safe, but excessive conservatism discourages exploration. How much behavior change is too much? We show how to use any safe reference policy as a probabilistic regulator for any optimized but untested policy. Conformal calibration on data from the safe policy determines how aggressively the new policy can act, while provably enforcing the user's declared risk tolerance. Unlike conservative optimization methods, we do not assume the user has identified the correct model class nor tuned any hyperparameters. Unlike previous conformal methods, our theory provides finite-sample guarantees even for non-monotonic bounded constraint functions. Our experiments on applications ranging from natural language question answering to biomolecular engineering show that safe exploration is not only possible from the first moment of deployment, but can also improve performance.

Testing For Distribution Shifts with Conditional Conformal Test Martingales

We propose a sequential test for detecting arbitrary distribution shifts that allows conformal test martingales (CTMs) to work under a fixed, reference-conditional setting. Existing CTM detectors construct test martingales by continually growing a reference set with each incoming sample, using it to assess how atypical the new sample is relative to past observations. While this design yields anytime-valid type-I error control, it suffers from test-time contamination: after a change, post-shift observations enter the reference set and dilute the evidence for distribution shift, increasing detection delay and reducing power. In contrast, our method avoids contamination by design by comparing each new sample to a fixed null reference dataset. Our main technical contribution is a robust martingale construction that remains valid conditional on the null reference data, achieved by explicitly accounting for the estimation error in the reference distribution induced by the finite reference set. This yields anytime-valid type-I error control together with guarantees of asymptotic power one and bounded expected detection delay. Empirically, our method detects shifts faster than standard CTMs, providing a powerful and reliable distribution-shift detector.

Improving Coverage in Combined Prediction Sets with Weighted p-values

Conformal prediction quantifies the uncertainty of machine learning models by augmenting point predictions with valid prediction sets, assuming exchangeability. For complex scenarios involving multiple trials, models, or data sources, conformal prediction sets can be aggregated to create a prediction set that captures the overall uncertainty, often improving precision. However, aggregating multiple prediction sets with individual $1-\alpha$ coverage inevitably weakens the overall guarantee, typically resulting in $1-2\alpha$ worst-case coverage. In this work, we propose a framework for the weighted aggregation of prediction sets, where weights are assigned to each prediction set based on their contribution. Our framework offers flexible control over how the sets are aggregated, achieving tighter coverage bounds that interpolate between the $1-2\alpha$ guarantee of the combined models and the $1-\alpha$ guarantee of an individual model depending on the distribution of weights. We extend our framework to data-dependent weights, and we derive a general procedure for data-dependent weight aggregation that maintains finite-sample validity. We demonstrate the effectiveness of our methods through experiments on synthetic and real data in the mixture-of-experts setting, and we show that aggregation with data-dependent weights provides a form of adaptive coverage.

WATCH: Adaptive Monitoring for AI Deployments via Weighted-Conformal Martingales

Responsibly deploying artificial intelligence (AI) / machine learning (ML) systems in high-stakes settings arguably requires not only proof of system reliability, but moreover continual, post-deployment monitoring to quickly detect and address any unsafe behavior. Statistical methods for nonparametric change-point detection -- especially the tools of conformal test martingales (CTMs) and anytime-valid inference -- offer promising approaches to this monitoring task. However, existing methods are restricted to monitoring limited hypothesis classes or ``alarm criteria'' (such as data shifts that violate certain exchangeability assumptions), do not allow for online adaptation in response to shifts, and/or do not enable root-cause analysis of any degradation. In this paper, we expand the scope of these monitoring methods by proposing a weighted generalization of conformal test martingales (WCTMs), which lay a theoretical foundation for online monitoring for any unexpected changepoints in the data distribution while controlling false-alarms. For practical applications, we propose specific WCTM algorithms that adapt online to mild covariate shifts (in the marginal input distribution) while quickly detecting and diagnosing more severe shifts, such as concept shifts (in the conditional label distribution) or extreme (out-of-support) covariate shifts that cannot be easily adapted to. On real-world datasets, we demonstrate improved performance relative to state-of-the-art baselines.

WATCH: Weighted Adaptive Testing for Changepoint Hypotheses via Weighted-Conformal Martingales

Responsibly deploying artificial intelligence (AI) / machine learning (ML) systems in high-stakes settings arguably requires not only proof of system reliability, but moreover continual, post-deployment monitoring to quickly detect and address any unsafe behavior. Statistical methods for nonparametric change-point detection -- especially the tools of conformal test martingales (CTMs) and anytime-valid inference -- offer promising approaches to this monitoring task. However, existing methods are restricted to monitoring limited hypothesis classes or ``alarm criteria,'' such as data shifts that violate certain exchangeability assumptions, or do not allow for online adaptation in response to shifts. In this paper, we expand the scope of these monitoring methods by proposing a weighted generalization of conformal test martingales (WCTMs), which lay a theoretical foundation for online monitoring for any unexpected changepoints in the data distribution while controlling false-alarms. For practical applications, we propose specific WCTM algorithms that accommodate online adaptation to mild covariate shifts (in the marginal input distribution) while raising alarms in response to more severe shifts, such as concept shifts (in the conditional label distribution) or extreme (out-of-support) covariate shifts that cannot be easily adapted to. On real-world datasets, we demonstrate improved performance relative to state-of-the-art baselines.

Conformal Validity Guarantees Exist for Any Data Distribution

As machine learning (ML) gains widespread adoption, practitioners are increasingly seeking means to quantify and control the risk these systems incur. This challenge is especially salient when ML systems have autonomy to collect their own data, such as in black-box optimization and active learning, where their actions induce sequential feedback-loop shifts in the data distribution. Conformal prediction has emerged as a promising approach to uncertainty and risk quantification, but existing variants either fail to accommodate sequences of data-dependent shifts, or do not fully exploit the fact that agent-induced shift is under our control. In this work we prove that conformal prediction can theoretically be extended to \textit{any} joint data distribution, not just exchangeable or quasi-exchangeable ones, although it is exceedingly impractical to compute in the most general case. For practical applications, we outline a procedure for deriving specific conformal algorithms for any data distribution, and we use this procedure to derive tractable algorithms for a series of agent-induced covariate shifts. We evaluate the proposed algorithms empirically on synthetic black-box optimization and active learning tasks.

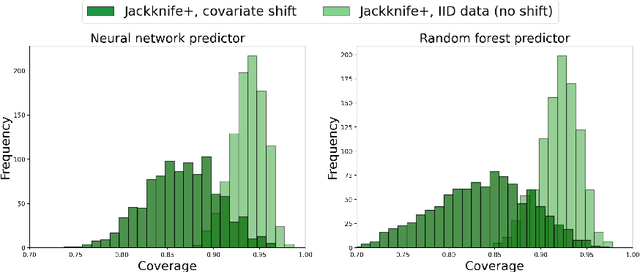
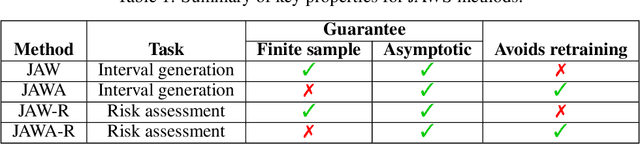
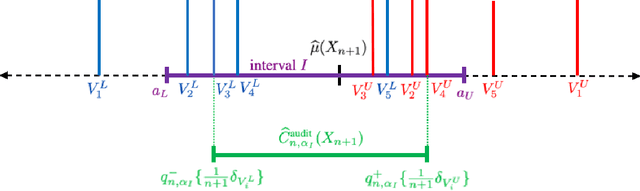
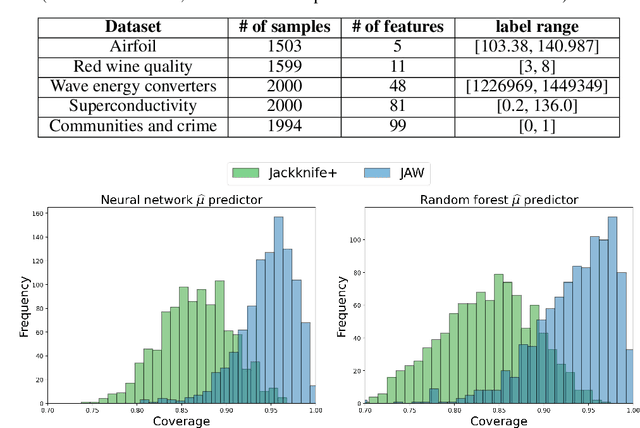
JAWS: Predictive Inference Under Covariate Shift

We propose \textbf{JAWS}, a series of wrapper methods for distribution-free uncertainty quantification tasks under covariate shift, centered on our core method \textbf{JAW}, the \textbf{JA}ckknife+ \textbf{W}eighted with likelihood-ratio weights. JAWS also includes computationally efficient \textbf{A}pproximations of JAW using higher-order influence functions: \textbf{JAWA}. Theoretically, we show that JAW relaxes the jackknife+'s assumption of data exchangeability to achieve the same finite-sample coverage guarantee even under covariate shift. JAWA further approaches the JAW guarantee in the limit of either the sample size or the influence function order under mild assumptions. Moreover, we propose a general approach to repurposing any distribution-free uncertainty quantification method and its guarantees to the task of risk assessment: a task that generates the estimated probability that the true label lies within a user-specified interval. We then propose \textbf{JAW-R} and \textbf{JAWA-R} as the repurposed versions of proposed methods for \textbf{R}isk assessment. Practically, JAWS outperform the state-of-the-art predictive inference baselines in a variety of biased real world data sets for both interval-generation and risk-assessment auditing tasks.