TS-CHIEF: A Scalable and Accurate Forest Algorithm for Time Series Classification

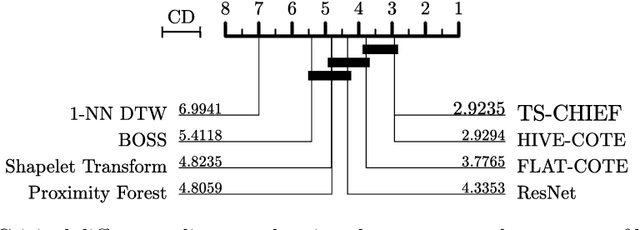
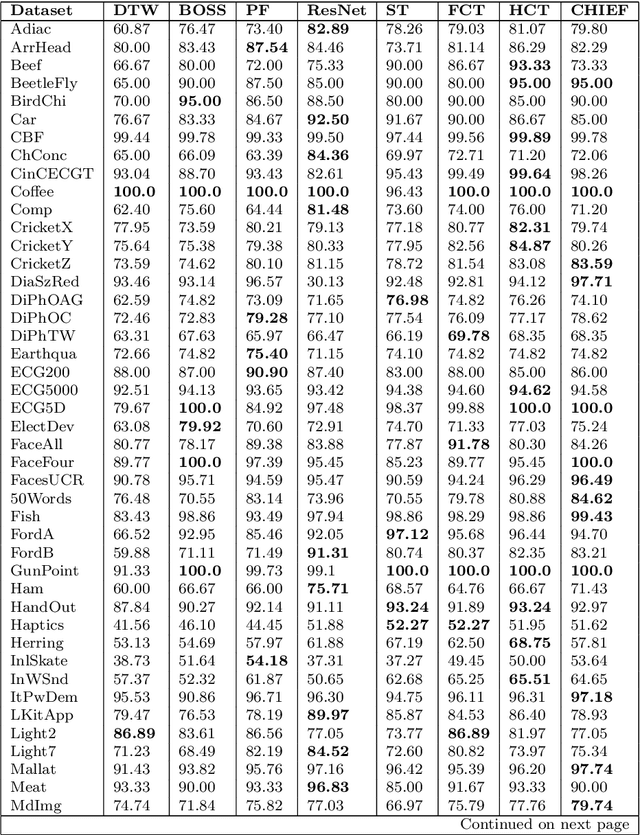
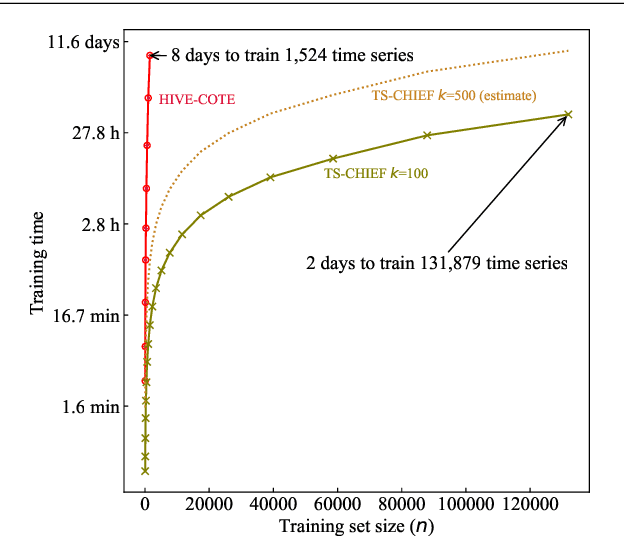
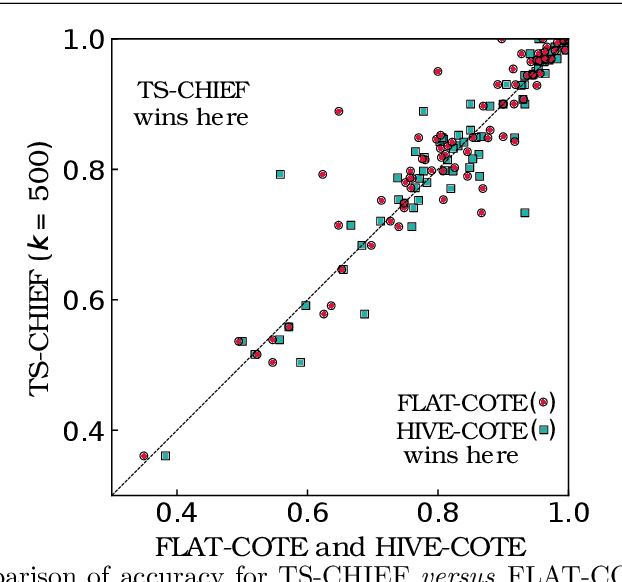
Time Series Classification (TSC) has seen enormous progress over the last two decades. HIVE-COTE (Hierarchical Vote Collective of Transformation-based Ensembles) is the current state of the art in terms of classification accuracy. HIVE-COTE recognizes that time series are a specific data type for which the traditional attribute-value representation, used predominantly in machine learning, fails to provide a relevant representation. HIVE-COTE combines multiple types of classifiers: each extracting information about a specific aspect of a time series, be it in the time domain, frequency domain or summarization of intervals within the series. However, HIVE-COTE (and its predecessor, FLAT-COTE) is often infeasible to run on even modest amounts of data. For instance, training HIVE-COTE on a dataset with only 1,500 time series can require 8 days of CPU time. It has polynomial runtime w.r.t training set size, so this problem compounds as data quantity increases. We propose a novel TSC algorithm, TS-CHIEF, which is highly competitive to HIVE-COTE in accuracy, but requires only a fraction of the runtime. TS-CHIEF constructs an ensemble classifier that integrates the most effective embeddings of time series that research has developed in the last decade. It uses tree-structured classifiers to do so efficiently. We assess TS-CHIEF on 85 datasets of the UCR archive, where it achieves state-of-the-art accuracy with scalability and efficiency. We demonstrate that TS-CHIEF can be trained on 130k time series in 2 days, a data quantity that is beyond the reach of any TSC algorithm with comparable accuracy.

Temporal Convolutional Neural Network for the Classification of Satellite Image Time Series

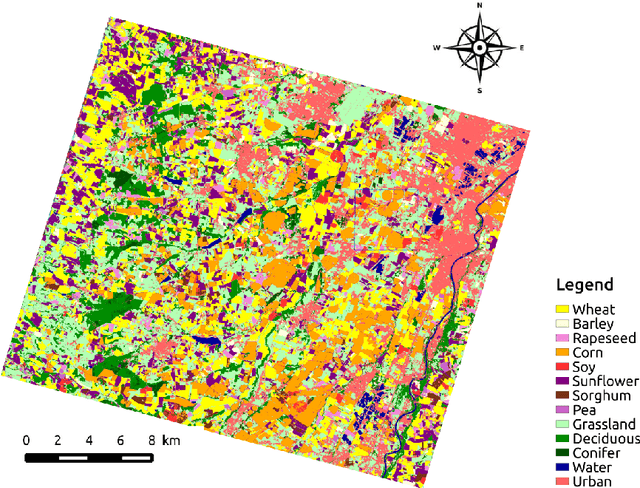
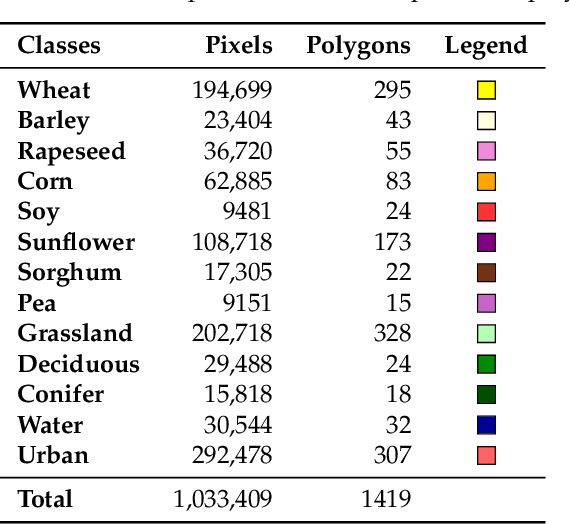
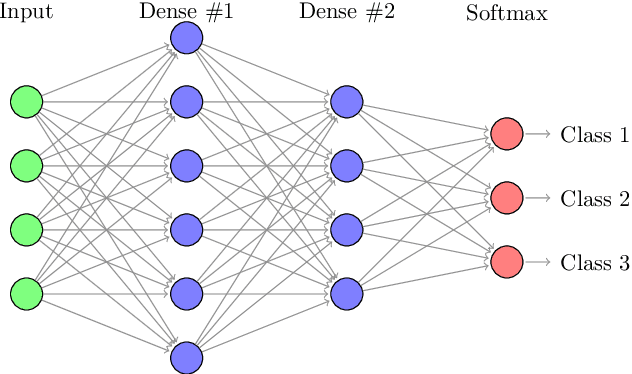
New remote sensing sensors acquire now high spatial and spectral Satellite Image Time Series (SITS) of the world. These series of images are a key component of any classification framework to obtain up-to-date and accurate land cover maps of the Earth's soils. More specifically, the combination of the temporal, spectral and spatial resolutions of new SITS enables the monitoring of vegetation dynamics. Although some traditional classification algorithms, such as Random Forest (RF), have been successfully applied for SITS classification, these algorithms do not fully take advantage of the temporal domain. Conversely, deep-learning based methods have been successfully used to make the most of sequential data such as text and audio data. For the first time, this paper explores the use of Convolutional Neural Networks (CNNs) with convolutions applied in the temporal dimension for SITS classification. The goal is to quantitatively and qualitatively evaluate the contribution of temporal CNNs for SITS classification. More precisely, this paper proposes a set of experiments performed on a million Formosat-2 time series. The experimental results show that temporal CNNs are 2 to 3 % more accurate than RF. The experiments also highlight some counter-intuitive results on pooling layers: contrary to image classification, their use decreases accuracy. Moreover, we provide some general guidelines on the network architecture, common regularization mechanisms, and hyper-parameter values such as the batch size. Finally, the visual quality of the land cover maps produced by the temporal CNN is assessed.

Elastic bands across the path: A new framework and methods to lower bound DTW

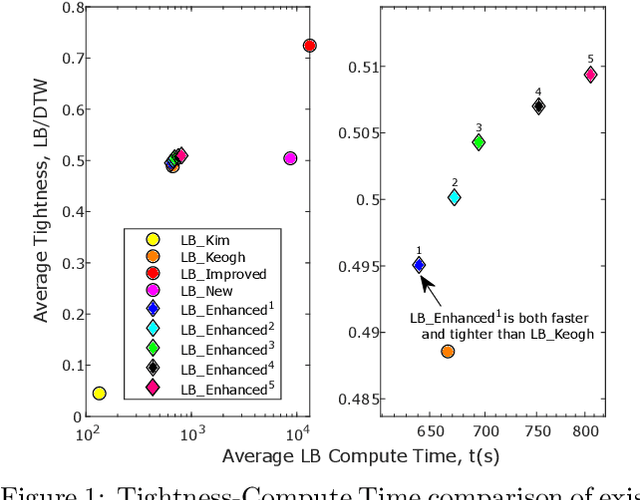
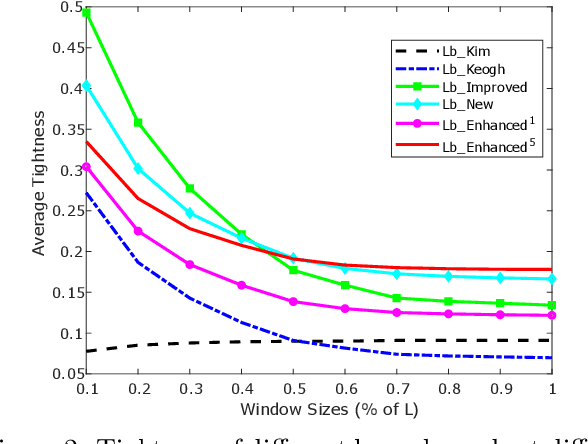
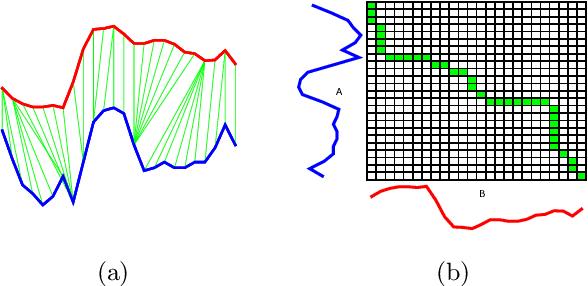
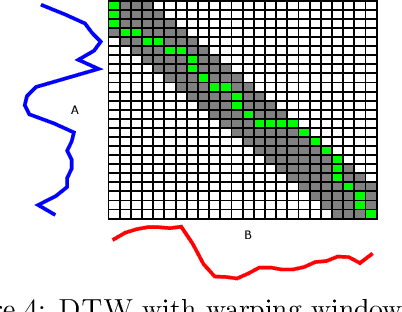
There has been renewed recent interest in developing effective lower bounds for Dynamic Time Warping (DTW) distance between time series. These have many applications in time series indexing, clustering, forecasting, regression and classification. One of the key time series classification algorithms, the nearest neighbor algorithm with DTW distance (NN-DTW) is very expensive to compute, due to the quadratic complexity of DTW. Lower bound search can speed up NN-DTW substantially. An effective and tight lower bound quickly prunes off unpromising nearest neighbor candidates from the search space and minimises the number of the costly DTW computations. The speed up provided by lower bound search becomes increasingly critical as training set size increases. Different lower bounds provide different trade-offs between computation time and tightness. Most existing lower bounds interact with DTW warping window sizes. They are very tight and effective at smaller warping window sizes, but become looser as the warping window increases, thus reducing the pruning effectiveness for NN-DTW. In this work, we present a new class of lower bounds that are tighter than the popular Keogh lower bound, while requiring similar computation time. Our new lower bounds take advantage of the DTW boundary condition, monotonicity and continuity constraints to create a tighter lower bound. Of particular significance, they remain relatively tight even for large windows. A single parameter to these new lower bounds controls the speed-tightness trade-off. We demonstrate that these new lower bounds provide an exceptional balance between computation time and tightness for the NN-DTW time series classification task, resulting in greatly improved efficiency for NN-DTW lower bound search.

Proximity Forest: An effective and scalable distance-based classifier for time series

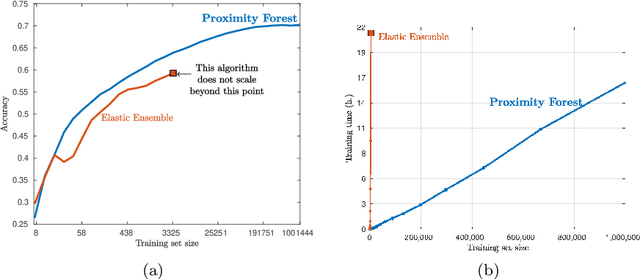
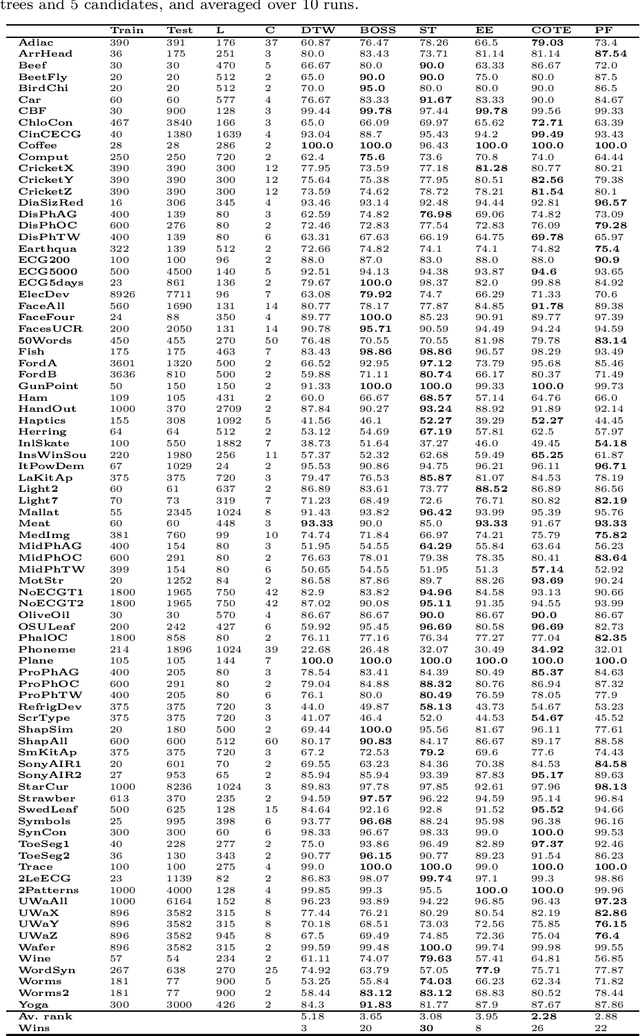
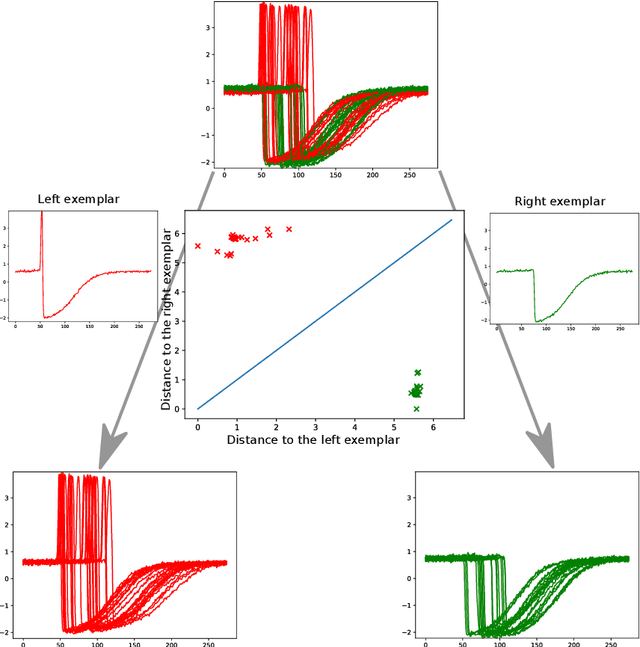
Research into the classification of time series has made enormous progress in the last decade. The UCR time series archive has played a significant role in challenging and guiding the development of new learners for time series classification. The largest dataset in the UCR archive holds 10 thousand time series only; which may explain why the primary research focus has been in creating algorithms that have high accuracy on relatively small datasets. This paper introduces Proximity Forest, an algorithm that learns accurate models from datasets with millions of time series, and classifies a time series in milliseconds. The models are ensembles of highly randomized Proximity Trees. Whereas conventional decision trees branch on attribute values (and usually perform poorly on time series), Proximity Trees branch on the proximity of time series to one exemplar time series or another; allowing us to leverage the decades of work into developing relevant measures for time series. Proximity Forest gains both efficiency and accuracy by stochastic selection of both exemplars and similarity measures. Our work is motivated by recent time series applications that provide orders of magnitude more time series than the UCR benchmarks. Our experiments demonstrate that Proximity Forest is highly competitive on the UCR archive: it ranks among the most accurate classifiers while being significantly faster. We demonstrate on a 1M time series Earth observation dataset that Proximity Forest retains this accuracy on datasets that are many orders of magnitude greater than those in the UCR repository, while learning its models at least 100,000 times faster than current state of the art models Elastic Ensemble and COTE.

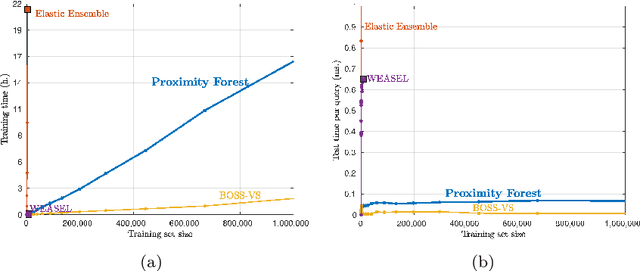
An Incremental Construction of Deep Neuro Fuzzy System for Continual Learning of Non-stationary Data Streams

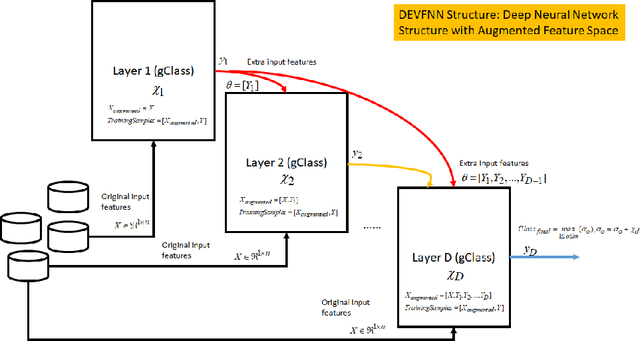
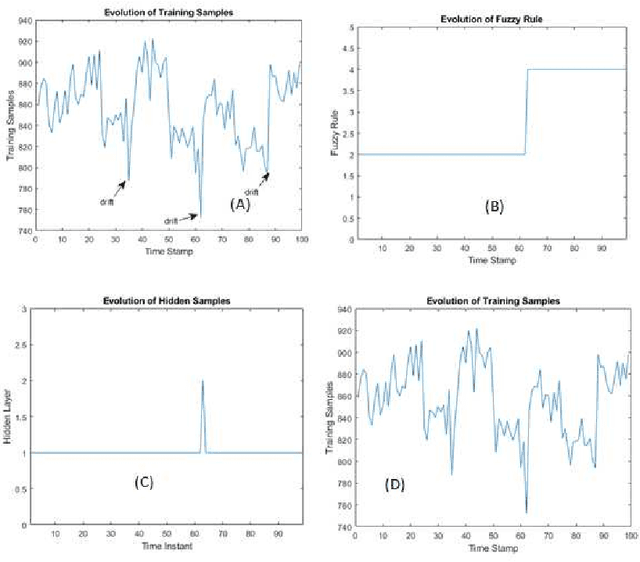
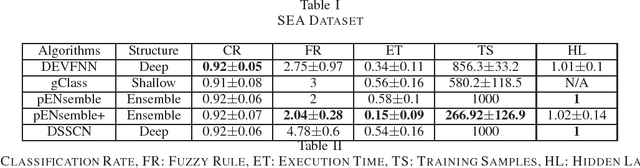
Existing fuzzy neural networks (FNNs) are mostly developed under a shallow network configuration having lower generalization power than those of deep structures. This paper proposes a novel self-organizing deep fuzzy neural network, namely deep evolving fuzzy neural networks (DEVFNN). Fuzzy rules can be automatically extracted from data streams or removed if they play little role during their lifespan. The structure of the network can be deepened on demand by stacking additional layers using a drift detection method which not only detects the covariate drift, variations of input space, but also accurately identifies the real drift, dynamic changes of both feature space and target space. DEVFNN is developed under the stacked generalization principle via the feature augmentation concept where a recently developed algorithm, namely Generic Classifier (gClass), drives the hidden layer. It is equipped by an automatic feature selection method which controls activation and deactivation of input attributes to induce varying subsets of input features. A deep network simplification procedure is put forward using the concept of hidden layer merging to prevent uncontrollable growth of input space dimension due to the nature of feature augmentation approach in building a deep network structure. DEVFNN works in the sample-wise fashion and is compatible for data stream applications. The efficacy of DEVFNN has been thoroughly evaluated using six datasets with non-stationary properties under the prequential test-then-train protocol. It has been compared with four state-of the art data stream methods and its shallow counterpart where DEVFNN demonstrates improvement of classification accuracy.

Accurate parameter estimation for Bayesian Network Classifiers using Hierarchical Dirichlet Processes

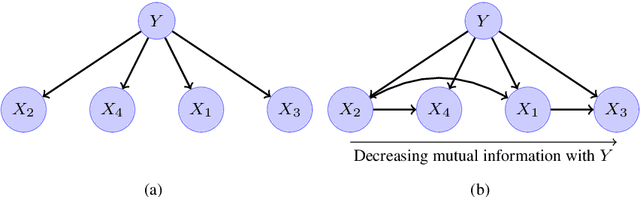
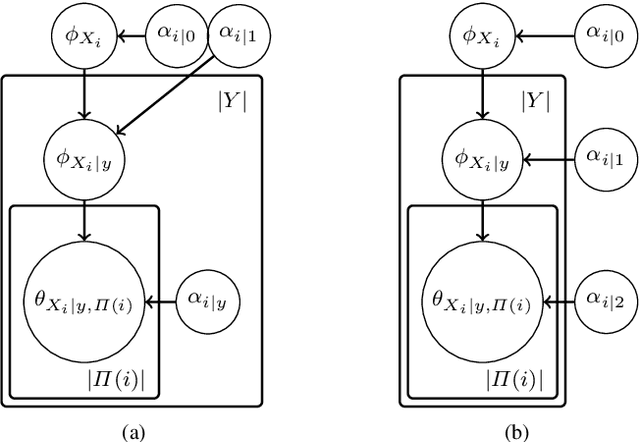
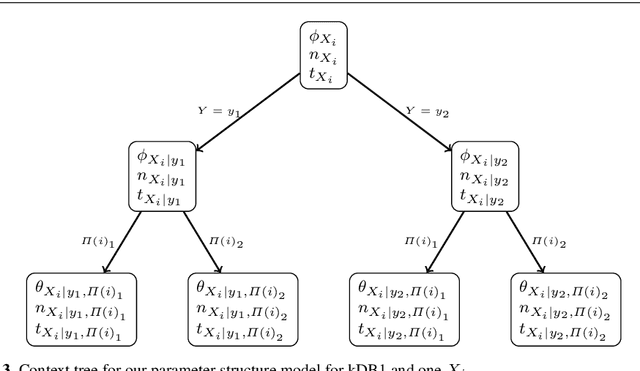
This paper introduces a novel parameter estimation method for the probability tables of Bayesian network classifiers (BNCs), using hierarchical Dirichlet processes (HDPs). The main result of this paper is to show that improved parameter estimation allows BNCs to outperform leading learning methods such as Random Forest for both 0-1 loss and RMSE, albeit just on categorical datasets. As data assets become larger, entering the hyped world of "big", efficient accurate classification requires three main elements: (1) classifiers with low-bias that can capture the fine-detail of large datasets (2) out-of-core learners that can learn from data without having to hold it all in main memory and (3) models that can classify new data very efficiently. The latest Bayesian network classifiers (BNCs) satisfy these requirements. Their bias can be controlled easily by increasing the number of parents of the nodes in the graph. Their structure can be learned out of core with a limited number of passes over the data. However, as the bias is made lower to accurately model classification tasks, so is the accuracy of their parameters' estimates, as each parameter is estimated from ever decreasing quantities of data. In this paper, we introduce the use of Hierarchical Dirichlet Processes for accurate BNC parameter estimation. We conduct an extensive set of experiments on 68 standard datasets and demonstrate that our resulting classifiers perform very competitively with Random Forest in terms of prediction, while keeping the out-of-core capability and superior classification time.

Skopus: Mining top-k sequential patterns under leverage

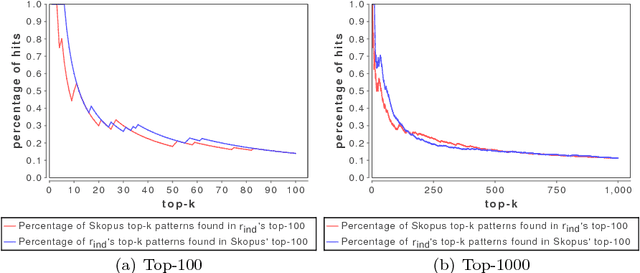
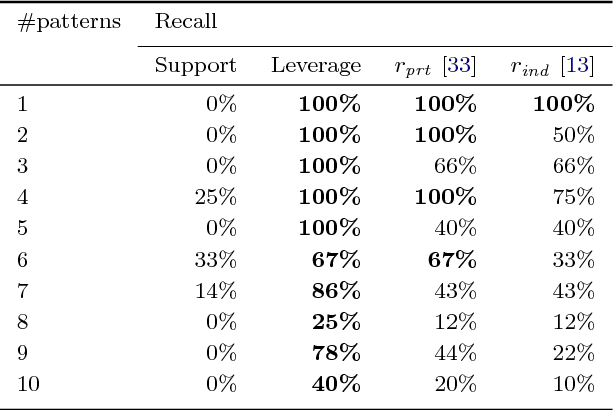
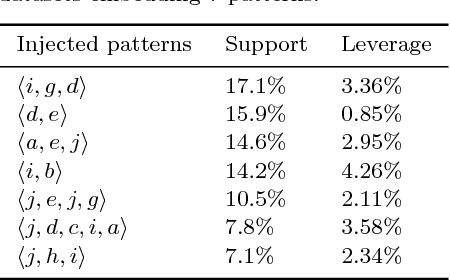
This paper presents a framework for exact discovery of the top-k sequential patterns under Leverage. It combines (1) a novel definition of the expected support for a sequential pattern - a concept on which most interestingness measures directly rely - with (2) SkOPUS: a new branch-and-bound algorithm for the exact discovery of top-k sequential patterns under a given measure of interest. Our interestingness measure employs the partition approach. A pattern is interesting to the extent that it is more frequent than can be explained by assuming independence between any of the pairs of patterns from which it can be composed. The larger the support compared to the expectation under independence, the more interesting is the pattern. We build on these two elements to exactly extract the k sequential patterns with highest leverage, consistent with our definition of expected support. We conduct experiments on both synthetic data with known patterns and real-world datasets; both experiments confirm the consistency and relevance of our approach with regard to the state of the art. This article was published in Data Mining and Knowledge Discovery and is accessible at http://dx.doi.org/10.1007/s10618-016-0467-9.

On the Inter-relationships among Drift rate, Forgetting rate, Bias/variance profile and Error

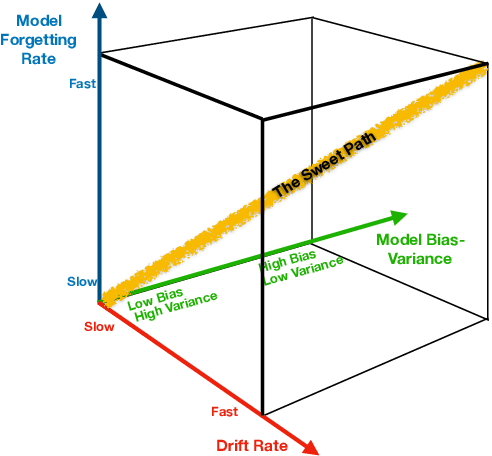
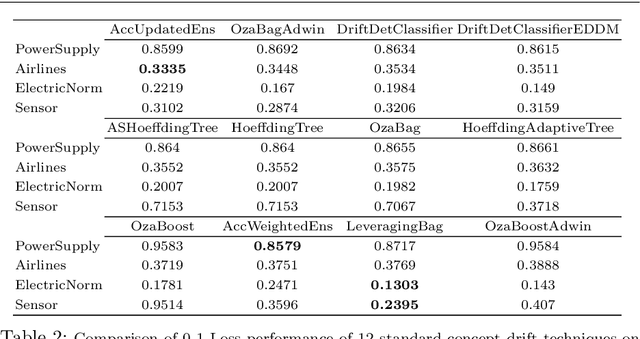
We propose two general and falsifiable hypotheses about expectations on generalization error when learning in the context of concept drift. One posits that as drift rate increases, the forgetting rate that minimizes generalization error will also increase and vice versa. The other posits that as a learner's forgetting rate increases, the bias/variance profile that minimizes generalization error will have lower variance and vice versa. These hypotheses lead to the concept of the sweet path, a path through the 3-d space of alternative drift rates, forgetting rates and bias/variance profiles on which generalization error will be minimized, such that slow drift is coupled with low forgetting and low bias, while rapid drift is coupled with fast forgetting and low variance. We present experiments that support the existence of such a sweet path. We also demonstrate that simple learners that select appropriate forgetting rates and bias/variance profiles are highly competitive with the state-of-the-art in incremental learners for concept drift on real-world drift problems.

Specious rules: an efficient and effective unifying method for removing misleading and uninformative patterns in association rule mining

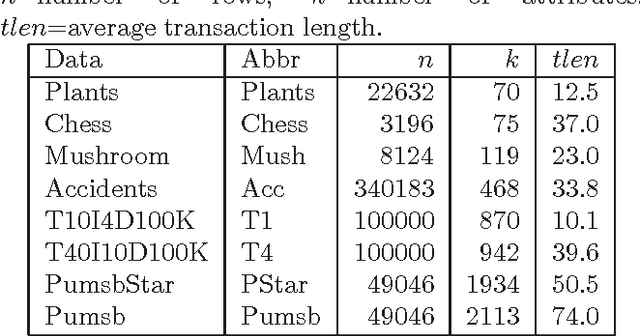
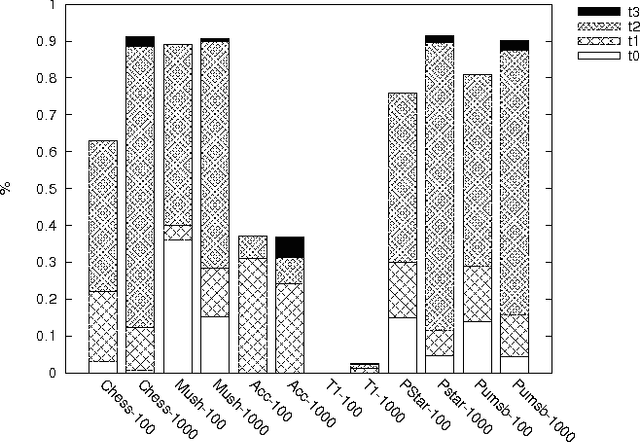
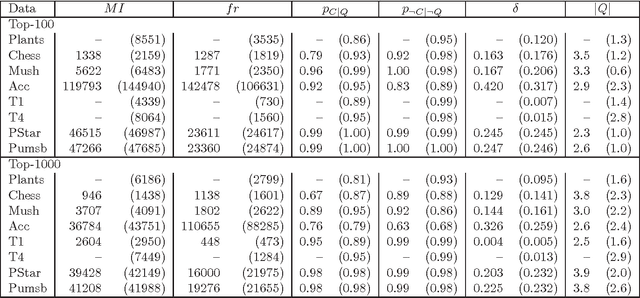
We present theoretical analysis and a suite of tests and procedures for addressing a broad class of redundant and misleading association rules we call \emph{specious rules}. Specious dependencies, also known as \emph{spurious}, \emph{apparent}, or \emph{illusory associations}, refer to a well-known phenomenon where marginal dependencies are merely products of interactions with other variables and disappear when conditioned on those variables. The most extreme example is Yule-Simpson's paradox where two variables present positive dependence in the marginal contingency table but negative in all partial tables defined by different levels of a confounding factor. It is accepted wisdom that in data of any nontrivial dimensionality it is infeasible to control for all of the exponentially many possible confounds of this nature. In this paper, we consider the problem of specious dependencies in the context of statistical association rule mining. We define specious rules and show they offer a unifying framework which covers many types of previously proposed redundant or misleading association rules. After theoretical analysis, we introduce practical algorithms for detecting and pruning out specious association rules efficiently under many key goodness measures, including mutual information and exact hypergeometric probabilities. We demonstrate that the procedure greatly reduces the number of associations discovered, providing an elegant and effective solution to the problem of association mining discovering large numbers of misleading and redundant rules.

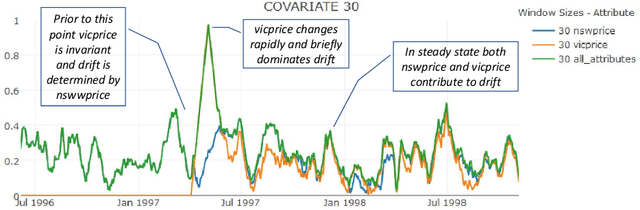
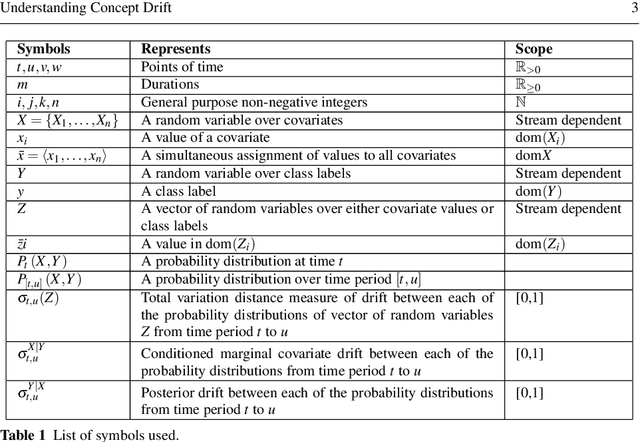
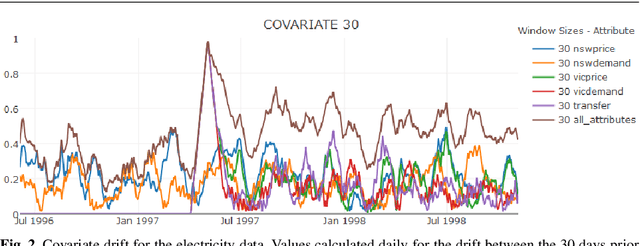
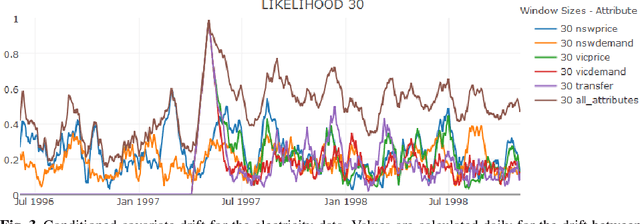
Understanding Concept Drift

Concept drift is a major issue that greatly affects the accuracy and reliability of many real-world applications of machine learning. We argue that to tackle concept drift it is important to develop the capacity to describe and analyze it. We propose tools for this purpose, arguing for the importance of quantitative descriptions of drift in marginal distributions. We present quantitative drift analysis techniques along with methods for communicating their results. We demonstrate their effectiveness by application to three real-world learning tasks.