Subspace Diffusion Generative Models

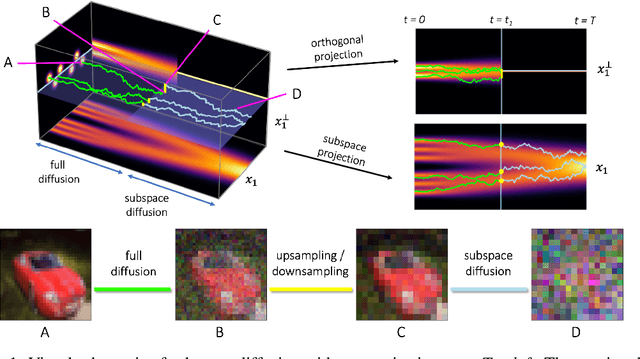
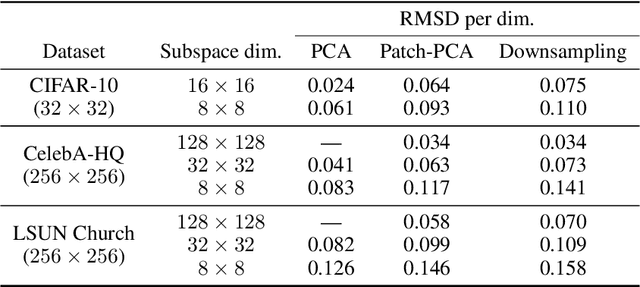
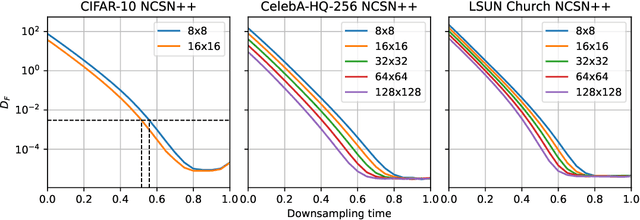
Score-based models generate samples by mapping noise to data (and vice versa) via a high-dimensional diffusion process. We question whether it is necessary to run this entire process at high dimensionality and incur all the inconveniences thereof. Instead, we restrict the diffusion via projections onto subspaces as the data distribution evolves toward noise. When applied to state-of-the-art models, our framework simultaneously improves sample quality -- reaching an FID of 2.17 on unconditional CIFAR-10 -- and reduces the computational cost of inference for the same number of denoising steps. Our framework is fully compatible with continuous-time diffusion and retains its flexible capabilities, including exact log-likelihoods and controllable generation. Code is available at https://github.com/bjing2016/subspace-diffusion.

Graph Anisotropic Diffusion

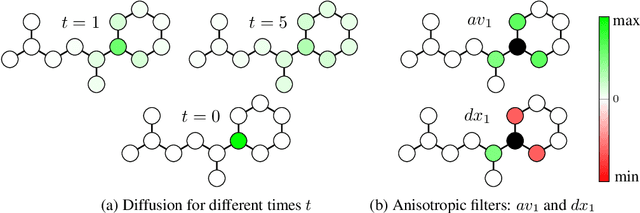
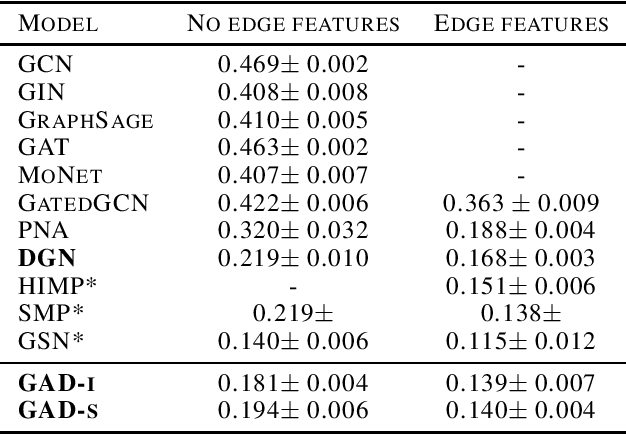
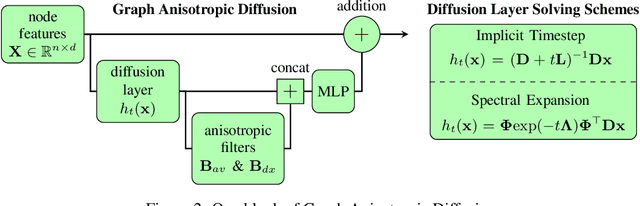
Traditional Graph Neural Networks (GNNs) rely on message passing, which amounts to permutation-invariant local aggregation of neighbour features. Such a process is isotropic and there is no notion of `direction' on the graph. We present a new GNN architecture called Graph Anisotropic Diffusion. Our model alternates between linear diffusion, for which a closed-form solution is available, and local anisotropic filters to obtain efficient multi-hop anisotropic kernels. We test our model on two common molecular property prediction benchmarks (ZINC and QM9) and show its competitive performance.

Neural Distance Embeddings for Biological Sequences

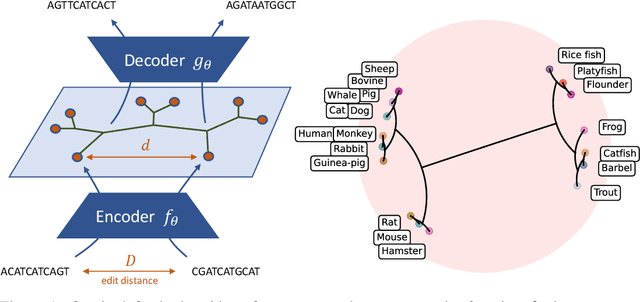
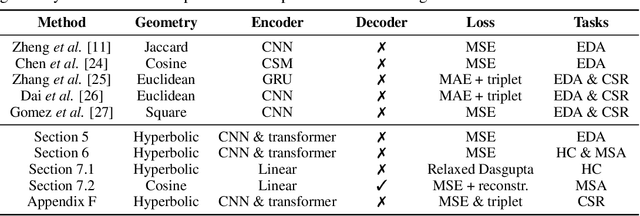
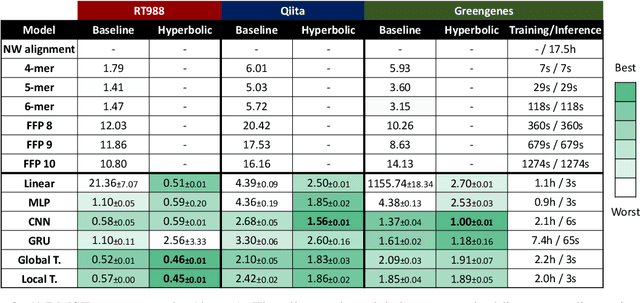
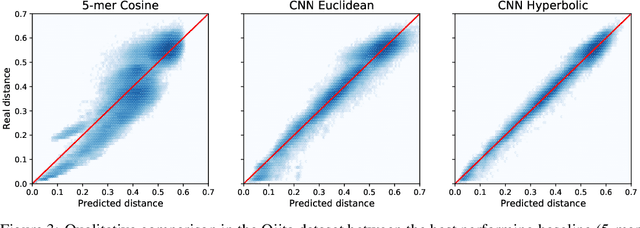
The development of data-dependent heuristics and representations for biological sequences that reflect their evolutionary distance is critical for large-scale biological research. However, popular machine learning approaches, based on continuous Euclidean spaces, have struggled with the discrete combinatorial formulation of the edit distance that models evolution and the hierarchical relationship that characterises real-world datasets. We present Neural Distance Embeddings (NeuroSEED), a general framework to embed sequences in geometric vector spaces, and illustrate the effectiveness of the hyperbolic space that captures the hierarchical structure and provides an average 22% reduction in embedding RMSE against the best competing geometry. The capacity of the framework and the significance of these improvements are then demonstrated devising supervised and unsupervised NeuroSEED approaches to multiple core tasks in bioinformatics. Benchmarked with common baselines, the proposed approaches display significant accuracy and/or runtime improvements on real-world datasets. As an example for hierarchical clustering, the proposed pretrained and from-scratch methods match the quality of competing baselines with 30x and 15x runtime reduction, respectively.

3D Infomax improves GNNs for Molecular Property Prediction

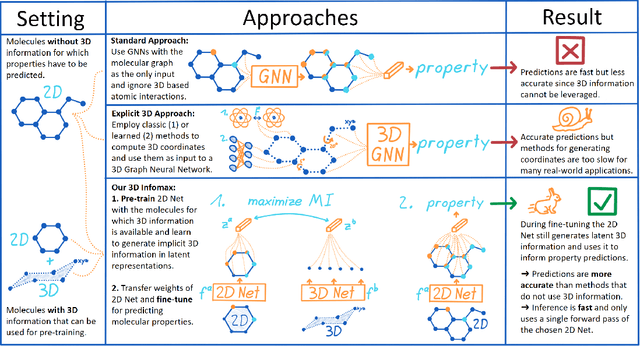
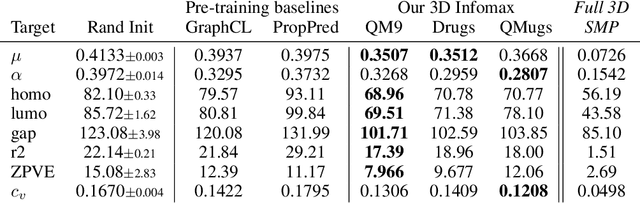
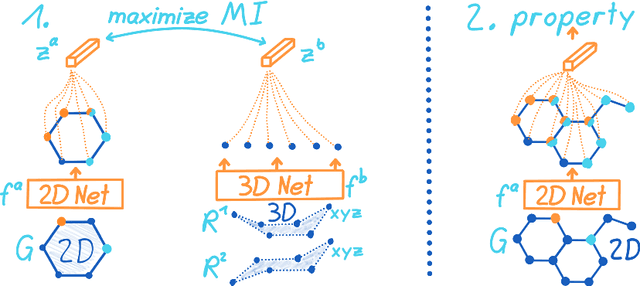
Molecular property prediction is one of the fastest-growing applications of deep learning with critical real-world impacts. Including 3D molecular structure as input to learned models their performance for many molecular tasks. However, this information is infeasible to compute at the scale required by several real-world applications. We propose pre-training a model to reason about the geometry of molecules given only their 2D molecular graphs. Using methods from self-supervised learning, we maximize the mutual information between 3D summary vectors and the representations of a Graph Neural Network (GNN) such that they contain latent 3D information. During fine-tuning on molecules with unknown geometry, the GNN still generates implicit 3D information and can use it to improve downstream tasks. We show that 3D pre-training provides significant improvements for a wide range of properties, such as a 22% average MAE reduction on eight quantum mechanical properties. Moreover, the learned representations can be effectively transferred between datasets in different molecular spaces.

Directional Graph Networks

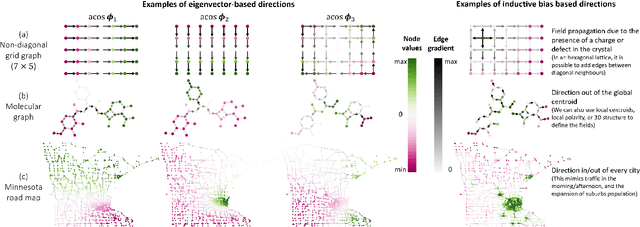
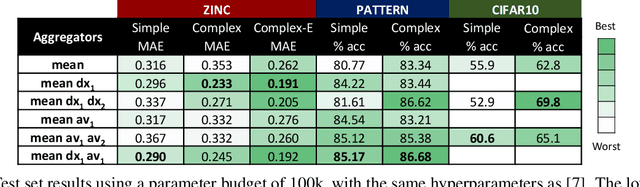
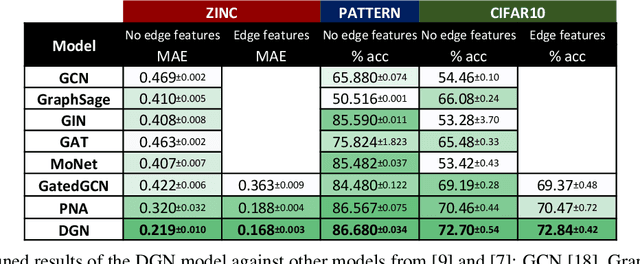
In order to overcome the expressive limitations of graph neural networks (GNNs), we propose the first method that exploits vector flows over graphs to develop globally consistent directional and asymmetric aggregation functions. We show that our directional graph networks (DGNs) generalize convolutional neural networks (CNNs) when applied on a grid. Whereas recent theoretical works focus on understanding local neighbourhoods, local structures and local isomorphism with no global information flow, our novel theoretical framework allows directional convolutional kernels in any graph. First, by defining a vector field in the graph, we develop a method of applying directional derivatives and smoothing by projecting node-specific messages into the field. Then we propose the use of the Laplacian eigenvectors as such vector field, and we show that the method generalizes CNNs on an n-dimensional grid. Finally, we bring the power of CNN data augmentation to graphs by providing a means of doing reflection, rotation and distortion on the underlying directional field. We evaluate our method on different standard benchmarks and see a relative error reduction of 8% on the CIFAR10 graph dataset and 11% to 32% on the molecular ZINC dataset. An important outcome of this work is that it enables to translate any physical or biological problems with intrinsic directional axes into a graph network formalism with an embedded directional field.

Principal Neighbourhood Aggregation for Graph Nets

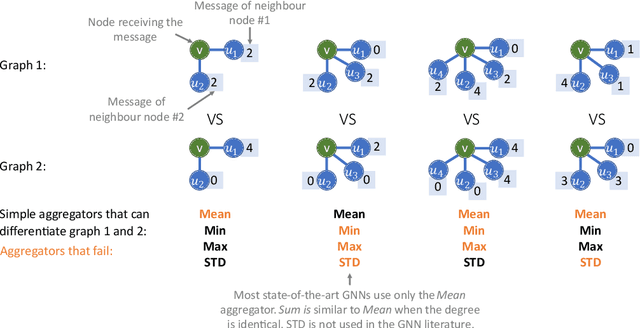
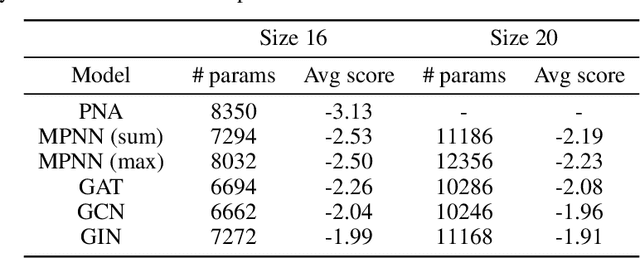
Graph Neural Networks (GNNs) have been shown to be effective models for different predictive tasks on graph-structured data. Recent work on their expressive power has focused on isomorphism tasks and countable feature spaces. We extend this theoretical framework to include continuous features - which occur regularly in real-world input domains and within the hidden layers of GNNs - and we demonstrate the requirement for multiple aggregation functions in this setting. Accordingly, we propose Principal Neighbourhood Aggregation (PNA), a novel architecture combining multiple aggregators with degree-scalers (which generalize the sum aggregator). Finally, we compare the capacity of different models to capture and exploit the graph structure via a benchmark containing multiple tasks taken from classical graph theory, which demonstrates the capacity of our model.