Leaf Stripping on Uniform Attachment Trees

In this note we analyze the performance of a simple root-finding algorithm in uniform attachment trees. The leaf-stripping algorithm recursively removes all leaves of the tree for a carefully chosen number of rounds. We show that, with probability $1 - \epsilon$, the set of remaining vertices contains the root and has a size only depending on $\epsilon$ but not on the size of the tree.

Uncertainty quantification in metric spaces

This paper introduces a novel uncertainty quantification framework for regression models where the response takes values in a separable metric space, and the predictors are in a Euclidean space. The proposed algorithms can efficiently handle large datasets and are agnostic to the predictive base model used. Furthermore, the algorithms possess asymptotic consistency guarantees and, in some special homoscedastic cases, we provide non-asymptotic guarantees. To illustrate the effectiveness of the proposed uncertainty quantification framework, we use a linear regression model for metric responses (known as the global Fr\'echet model) in various clinical applications related to precision and digital medicine. The different clinical outcomes analyzed are represented as complex statistical objects, including multivariate Euclidean data, Laplacian graphs, and probability distributions.

Estimating the history of a random recursive tree

This paper studies the problem of estimating the order of arrival of the vertices in a random recursive tree. Specifically, we study two fundamental models: the uniform attachment model and the linear preferential attachment model. We propose an order estimator based on the Jordan centrality measure and define a family of risk measures to quantify the quality of the ordering procedure. Moreover, we establish a minimax lower bound for this problem, and prove that the proposed estimator is nearly optimal. Finally, we numerically demonstrate that the proposed estimator outperforms degree-based and spectral ordering procedures.

On the quality of randomized approximations of Tukey's depth

Tukey's depth (or halfspace depth) is a widely used measure of centrality for multivariate data. However, exact computation of Tukey's depth is known to be a hard problem in high dimensions. As a remedy, randomized approximations of Tukey's depth have been proposed. In this paper we explore when such randomized algorithms return a good approximation of Tukey's depth. We study the case when the data are sampled from a log-concave isotropic distribution. We prove that, if one requires that the algorithm runs in polynomial time in the dimension, the randomized algorithm correctly approximates the maximal depth $1/2$ and depths close to zero. On the other hand, for any point of intermediate depth, any good approximation requires exponential complexity.

Online-to-PAC Conversions: Generalization Bounds via Regret Analysis

We present a new framework for deriving bounds on the generalization bound of statistical learning algorithms from the perspective of online learning. Specifically, we construct an online learning game called the "generalization game", where an online learner is trying to compete with a fixed statistical learning algorithm in predicting the sequence of generalization gaps on a training set of i.i.d. data points. We establish a connection between the online and statistical learning setting by showing that the existence of an online learning algorithm with bounded regret in this game implies a bound on the generalization error of the statistical learning algorithm, up to a martingale concentration term that is independent of the complexity of the statistical learning method. This technique allows us to recover several standard generalization bounds including a range of PAC-Bayesian and information-theoretic guarantees, as well as generalizations thereof.

Archaeology of random recursive dags and Cooper-Frieze random networks

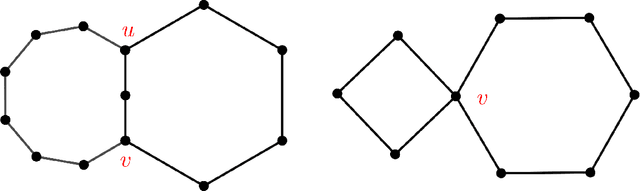
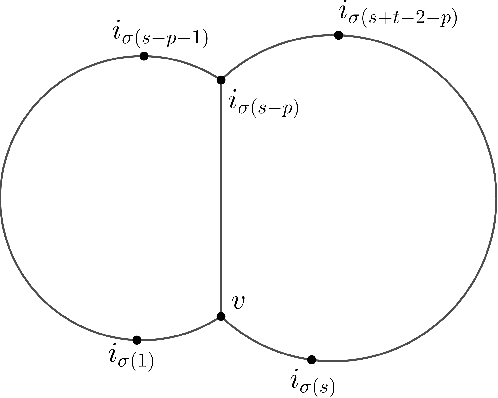
We study the problem of finding the root vertex in large growing networks. We prove that it is possible to construct confidence sets of size independent of the number of vertices in the network that contain the root vertex with high probability in various models of random networks. The models include uniform random recursive dags and uniform Cooper-Frieze random graphs.

Generalization Bounds via Convex Analysis

Since the celebrated works of Russo and Zou (2016,2019) and Xu and Raginsky (2017), it has been well known that the generalization error of supervised learning algorithms can be bounded in terms of the mutual information between their input and the output, given that the loss of any fixed hypothesis has a subgaussian tail. In this work, we generalize this result beyond the standard choice of Shannon's mutual information to measure the dependence between the input and the output. Our main result shows that it is indeed possible to replace the mutual information by any strongly convex function of the joint input-output distribution, with the subgaussianity condition on the losses replaced by a bound on an appropriately chosen norm capturing the geometry of the dependence measure. This allows us to derive a range of generalization bounds that are either entirely new or strengthen previously known ones. Examples include bounds stated in terms of $p$-norm divergences and the Wasserstein-2 distance, which are respectively applicable for heavy-tailed loss distributions and highly smooth loss functions. Our analysis is entirely based on elementary tools from convex analysis by tracking the growth of a potential function associated with the dependence measure and the loss function.

Bandit problems with fidelity rewards

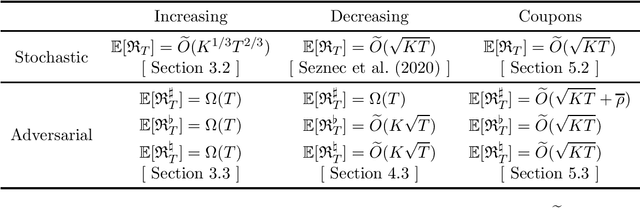
The fidelity bandits problem is a variant of the $K$-armed bandit problem in which the reward of each arm is augmented by a fidelity reward that provides the player with an additional payoff depending on how 'loyal' the player has been to that arm in the past. We propose two models for fidelity. In the loyalty-points model the amount of extra reward depends on the number of times the arm has previously been played. In the subscription model the additional reward depends on the current number of consecutive draws of the arm. We consider both stochastic and adversarial problems. Since single-arm strategies are not always optimal in stochastic problems, the notion of regret in the adversarial setting needs careful adjustment. We introduce three possible notions of regret and investigate which can be bounded sublinearly. We study in detail the special cases of increasing, decreasing and coupon (where the player gets an additional reward after every $m$ plays of an arm) fidelity rewards. For the models which do not necessarily enjoy sublinear regret, we provide a worst case lower bound. For those models which exhibit sublinear regret, we provide algorithms and bound their regret.

Learning to maximize global influence from local observations

We study a family online influence maximization problems where in a sequence of rounds $t=1,\ldots,T$, a decision maker selects one from a large number of agents with the goal of maximizing influence. Upon choosing an agent, the decision maker shares a piece of information with the agent, which information then spreads in an unobserved network over which the agents communicate. The goal of the decision maker is to select the sequence of agents in a way that the total number of influenced nodes in the network. In this work, we consider a scenario where the networks are generated independently for each $t$ according to some fixed but unknown distribution, so that the set of influenced nodes corresponds to the connected component of the random graph containing the vertex corresponding to the selected agent. Furthermore, we assume that the decision maker only has access to limited feedback: instead of making the unrealistic assumption that the entire network is observable, we suppose that the available feedback is generated based on a small neighborhood of the selected vertex. Our results show that such partial local observations can be sufficient for maximizing global influence. We model the underlying random graph as a sparse inhomogeneous Erd\H{o}s--R\'enyi graph, and study three specific families of random graph models in detail: stochastic block models, Chung--Lu models and Kronecker random graphs. We show that in these cases one may learn to maximize influence by merely observing the degree of the selected vertex in the generated random graph. We propose sequential learning algorithms that aim at maximizing influence, and provide their theoretical analysis in both the subcritical and supercritical regimes of all considered models.

Benign Overfitting in Linear Regression

The phenomenon of benign overfitting is one of the key mysteries uncovered by deep learning methodology: deep neural networks seem to predict well, even with a perfect fit to noisy training data. Motivated by this phenomenon, we consider when a perfect fit to training data in linear regression is compatible with accurate prediction. We give a characterization of gaussian linear regression problems for which the minimum norm interpolating prediction rule has near-optimal prediction accuracy. The characterization is in terms of two notions of the effective rank of the data covariance. It shows that overparameterization is essential for benign overfitting in this setting: the number of directions in parameter space that are unimportant for prediction must significantly exceed the sample size.