Reducing the Cost of Quantum Chemical Data By Backpropagating Through Density Functional Theory

Density Functional Theory (DFT) accurately predicts the quantum chemical properties of molecules, but scales as $O(N_{\text{electrons}}^3)$. Sch\"utt et al. (2019) successfully approximate DFT 1000x faster with Neural Networks (NN). Arguably, the biggest problem one faces when scaling to larger molecules is the cost of DFT labels. For example, it took years to create the PCQ dataset (Nakata & Shimazaki, 2017) on which subsequent NNs are trained within a week. DFT labels molecules by minimizing energy $E(\cdot )$ as a "loss function." We bypass dataset creation by directly training NNs with $E(\cdot )$ as a loss function. For comparison, Sch\"utt et al. (2019) spent 626 hours creating a dataset on which they trained their NN for 160h, for a total of 786h; our method achieves comparable performance within 31h.

On Quantitative Evaluations of Counterfactuals

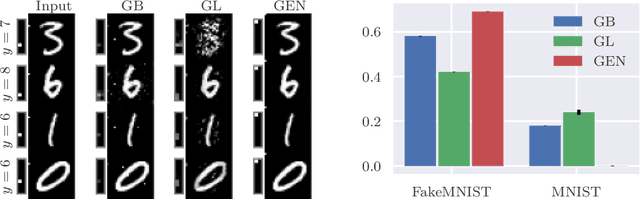
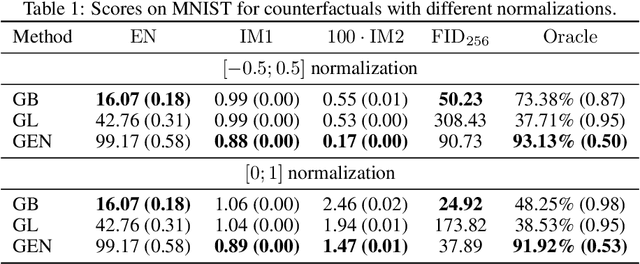
As counterfactual examples become increasingly popular for explaining decisions of deep learning models, it is essential to understand what properties quantitative evaluation metrics do capture and equally important what they do not capture. Currently, such understanding is lacking, potentially slowing down scientific progress. In this paper, we consolidate the work on evaluating visual counterfactual examples through an analysis and experiments. We find that while most metrics behave as intended for sufficiently simple datasets, some fail to tell the difference between good and bad counterfactuals when the complexity increases. We observe experimentally that metrics give good scores to tiny adversarial-like changes, wrongly identifying such changes as superior counterfactual examples. To mitigate this issue, we propose two new metrics, the Label Variation Score and the Oracle score, which are both less vulnerable to such tiny changes. We conclude that a proper quantitative evaluation of visual counterfactual examples should combine metrics to ensure that all aspects of good counterfactuals are quantified.

ECINN: Efficient Counterfactuals from Invertible Neural Networks

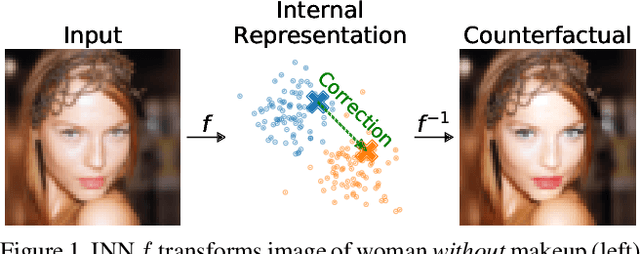
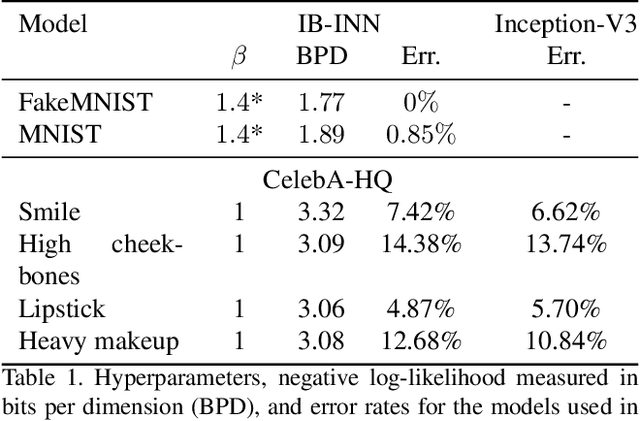
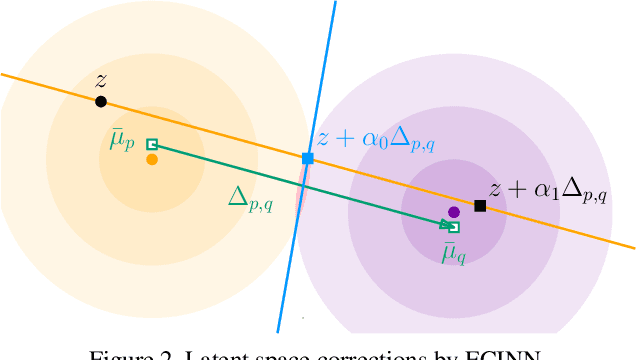
Counterfactual examples identify how inputs can be altered to change the predicted class of a classifier, thus opening up the black-box nature of, e.g., deep neural networks. We propose a method, ECINN, that utilizes the generative capacities of invertible neural networks for image classification to generate counterfactual examples efficiently. In contrast to competing methods that sometimes need a thousand evaluations or more of the classifier, ECINN has a closed-form expression and generates a counterfactual in the time of only two evaluations. Arguably, the main challenge of generating counterfactual examples is to alter only input features that affect the predicted outcome, i.e., class-dependent features. Our experiments demonstrate how ECINN alters class-dependent image regions to change the perceptual and predicted class of the counterfactuals. Additionally, we extend ECINN to also produce heatmaps (ECINNh) for easy inspection of, e.g., pairwise class-dependent changes in the generated counterfactual examples. Experimentally, we find that ECINNh outperforms established methods that generate heatmap-based explanations.

One Reflection Suffice

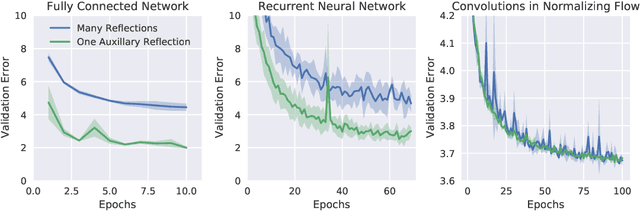
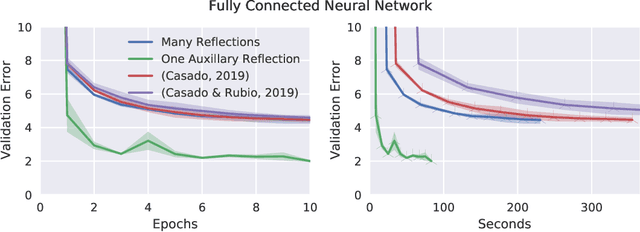
Orthogonal weight matrices are used in many areas of deep learning. Much previous work attempt to alleviate the additional computational resources it requires to constrain weight matrices to be orthogonal. One popular approach utilizes *many* Householder reflections. The only practical drawback is that many reflections cause low GPU utilization. We mitigate this final drawback by proving that *one* reflection is sufficient, if the reflection is computed by an auxiliary neural network.

Fast Fréchet Inception Distance

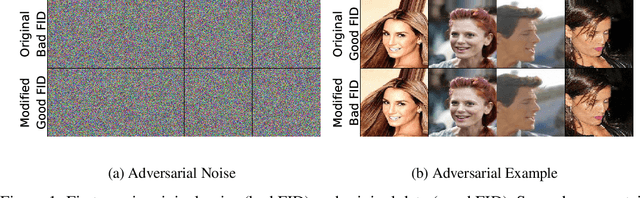
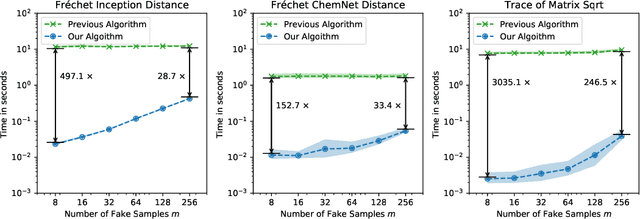
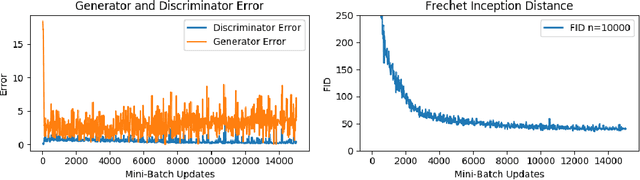
The Fr\'echet Inception Distance (FID) has been used to evaluate thousands of generative models. We present a novel algorithm, FastFID, which allows fast computation and backpropagation for FID. FastFID can efficiently (1) evaluate generative model *during* training and (2) construct adversarial examples for FID.

What if Neural Networks had SVDs?

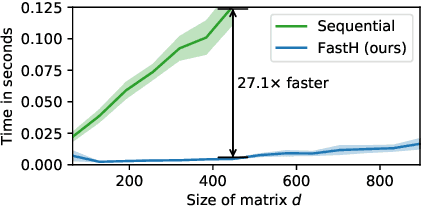
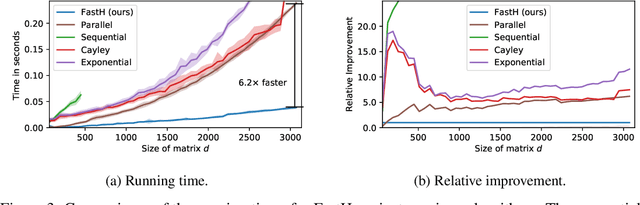
Various Neural Networks employ time-consuming matrix operations like matrix inversion. Many such matrix operations are faster to compute given the Singular Value Decomposition (SVD). Previous work allows using the SVD in Neural Networks without computing it. In theory, the techniques can speed up matrix operations, however, in practice, they are not fast enough. We present an algorithm that is fast enough to speed up several matrix operations. The algorithm increases the degree of parallelism of an underlying matrix multiplication $H\cdot X$ where $H$ is an orthogonal matrix represented by a product of Householder matrices. Code is available at www.github.com/AlexanderMath/fasth .

MeLIME: Meaningful Local Explanation for Machine Learning Models

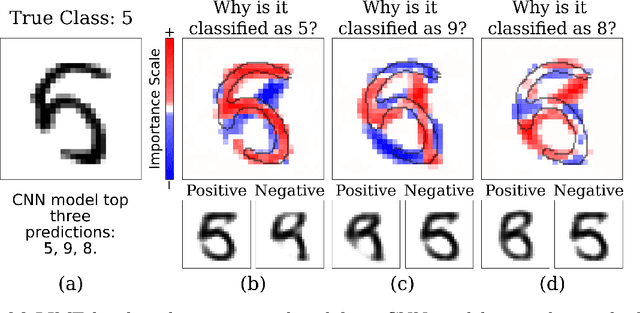
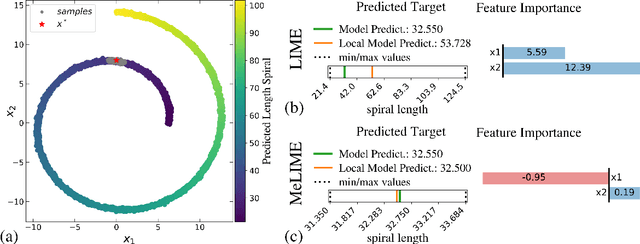
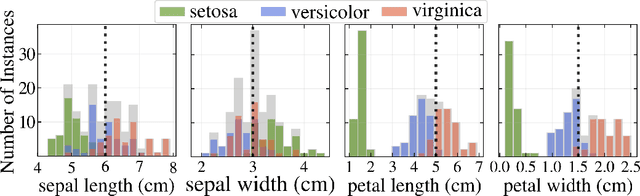
Most state-of-the-art machine learning algorithms induce black-box models, preventing their application in many sensitive domains. Hence, many methodologies for explaining machine learning models have been proposed to address this problem. In this work, we introduce strategies to improve local explanations taking into account the distribution of the data used to train the black-box models. We show that our approach, MeLIME, produces more meaningful explanations compared to other techniques over different ML models, operating on various types of data. MeLIME generalizes the LIME method, allowing more flexible perturbation sampling and the use of different local interpretable models. Additionally, we introduce modifications to standard training algorithms of local interpretable models fostering more robust explanations, even allowing the production of counterfactual examples. To show the strengths of the proposed approach, we include experiments on tabular data, images, and text; all showing improved explanations. In particular, MeLIME generated more meaningful explanations on the MNIST dataset than methods such as GuidedBackprop, SmoothGrad, and Layer-wise Relevance Propagation. MeLIME is available on https://github.com/tiagobotari/melime.