Frank Ban
Regularized Weighted Low Rank Approximation
Nov 19, 2019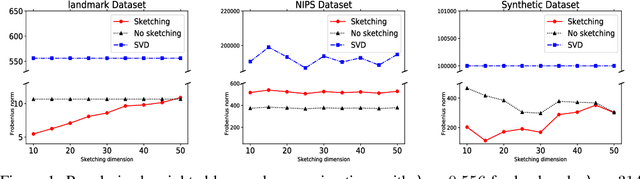
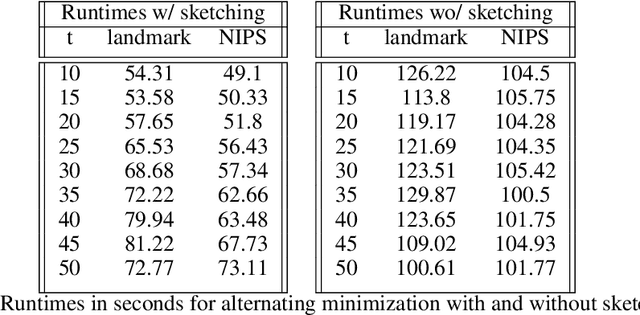
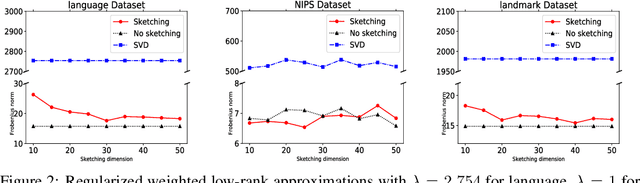
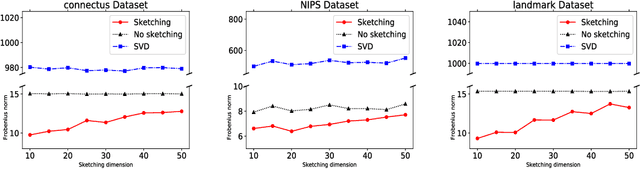
Abstract:The classical low rank approximation problem is to find a rank $k$ matrix $UV$ (where $U$ has $k$ columns and $V$ has $k$ rows) that minimizes the Frobenius norm of $A - UV$. Although this problem can be solved efficiently, we study an NP-hard variant of this problem that involves weights and regularization. A previous paper of [Razenshteyn et al. '16] derived a polynomial time algorithm for weighted low rank approximation with constant rank. We derive provably sharper guarantees for the regularized version by obtaining parameterized complexity bounds in terms of the statistical dimension rather than the rank, allowing for a rank-independent runtime that can be significantly faster. Our improvement comes from applying sharper matrix concentration bounds, using a novel conditioning technique, and proving structural theorems for regularized low rank problems.
Efficient average-case population recovery in the presence of insertions and deletions
Jul 12, 2019

Abstract:Several recent works have considered the \emph{trace reconstruction problem}, in which an unknown source string $x\in\{0,1\}^n$ is transmitted through a probabilistic channel which may randomly delete coordinates or insert random bits, resulting in a \emph{trace} of $x$. The goal is to reconstruct the original string~$x$ from independent traces of $x$. While the best algorithms known for worst-case strings use $\exp(O(n^{1/3}))$ traces \cite{DOS17,NazarovPeres17}, highly efficient algorithms are known \cite{PZ17,HPP18} for the \emph{average-case} version, in which $x$ is uniformly random. We consider a generalization of this average-case trace reconstruction problem, which we call \emph{average-case population recovery in the presence of insertions and deletions}. In this problem, there is an unknown distribution $\cal{D}$ over $s$ unknown source strings $x^1,\dots,x^s \in \{0,1\}^n$, and each sample is independently generated by drawing some $x^i$ from $\cal{D}$ and returning an independent trace of $x^i$. Building on \cite{PZ17} and \cite{HPP18}, we give an efficient algorithm for this problem. For any support size $s \leq \smash{\exp(\Theta(n^{1/3}))}$, for a $1-o(1)$ fraction of all $s$-element support sets $\{x^1,\dots,x^s\} \subset \{0,1\}^n$, for every distribution $\cal{D}$ supported on $\{x^1,\dots,x^s\}$, our algorithm efficiently recovers ${\cal D}$ up to total variation distance $\epsilon$ with high probability, given access to independent traces of independent draws from $\cal{D}$. The algorithm runs in time poly$(n,s,1/\epsilon)$ and its sample complexity is poly$(s,1/\epsilon,\exp(\log^{1/3}n)).$ This polynomial dependence on the support size $s$ is in sharp contrast with the \emph{worst-case} version (when $x^1,\dots,x^s$ may be any strings in $\{0,1\}^n$), in which the sample complexity of the most efficient known algorithm \cite{BCFSS19} is doubly exponential in $s$.
A PTAS for $\ell_p$-Low Rank Approximation
Jul 16, 2018Abstract:A number of recent works have studied algorithms for entrywise $\ell_p$-low rank approximation, namely algorithms which given an $n \times d$ matrix $A$ (with $n \geq d$), output a rank-$k$ matrix $B$ minimizing $\|A-B\|_p^p=\sum_{i,j} |A_{i,j} - B_{i,j}|^p$. We show the following: On the algorithmic side, for $p \in (0,2)$, we give the first $n^{\text{poly}(k/\epsilon)}$ time $(1+\epsilon)$-approximation algorithm. For $p = 0$, there are various problem formulations, a common one being the binary setting for which $A\in\{0,1\}^{n\times d}$ and $B = U \cdot V$, where $U\in\{0,1\}^{n \times k}$ and $V\in\{0,1\}^{k \times d}$. There are also various notions of multiplication $U \cdot V$, such as a matrix product over the reals, over a finite field, or over a Boolean semiring. We give the first PTAS for what we call the Generalized Binary $\ell_0$-Rank-$k$ Approximation problem, for which these variants are special cases. Our algorithm runs in time $(1/\epsilon)^{2^{O(k)}/\epsilon^{2}} \cdot nd \cdot \log^{2^k} d$. For the specific case of finite fields of constant size, we obtain an alternate algorithm with time $n \cdot d^{\text{poly}(k/\epsilon)}$. On the hardness front, for $p \in (1,2)$, we show under the Small Set Expansion Hypothesis and Exponential Time Hypothesis (ETH), there is no constant factor approximation algorithm running in time $2^{k^{\delta}}$ for a constant $\delta > 0$, showing an exponential dependence on $k$ is necessary. For $p = 0$, we observe that there is no approximation algorithm for the Generalized Binary $\ell_0$-Rank-$k$ Approximation problem running in time $2^{2^{\delta k}}$ for a constant $\delta > 0$. We also show for finite fields of constant size, under the ETH, that any fixed constant factor approximation algorithm requires $2^{k^{\delta}}$ time for a constant $\delta > 0$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge