Multilevel neural simulation-based inference

Neural simulation-based inference (SBI) is a popular set of methods for Bayesian inference when models are only available in the form of a simulator. These methods are widely used in the sciences and engineering, where writing down a likelihood can be significantly more challenging than constructing a simulator. However, the performance of neural SBI can suffer when simulators are computationally expensive, thereby limiting the number of simulations that can be performed. In this paper, we propose a novel approach to neural SBI which leverages multilevel Monte Carlo techniques for settings where several simulators of varying cost and fidelity are available. We demonstrate through both theoretical analysis and extensive experiments that our method can significantly enhance the accuracy of SBI methods given a fixed computational budget.

Stationary MMD Points for Cubature

Approximation of a target probability distribution using a finite set of points is a problem of fundamental importance, arising in cubature, data compression, and optimisation. Several authors have proposed to select points by minimising a maximum mean discrepancy (MMD), but the non-convexity of this objective precludes global minimisation in general. Instead, we consider \emph{stationary} points of the MMD which, in contrast to points globally minimising the MMD, can be accurately computed. Our main theoretical contribution is the (perhaps surprising) result that, for integrands in the associated reproducing kernel Hilbert space, the cubature error of stationary MMD points vanishes \emph{faster} than the MMD. Motivated by this \emph{super-convergence} property, we consider discretised gradient flows as a practical strategy for computing stationary points of the MMD, presenting a refined convergence analysis that establishes a novel non-asymptotic finite-particle error bound, which may be of independent interest.

Kernel Quantile Embeddings and Associated Probability Metrics

Embedding probability distributions into reproducing kernel Hilbert spaces (RKHS) has enabled powerful nonparametric methods such as the maximum mean discrepancy (MMD), a statistical distance with strong theoretical and computational properties. At its core, the MMD relies on kernel mean embeddings to represent distributions as mean functions in RKHS. However, it remains unclear if the mean function is the only meaningful RKHS representation. Inspired by generalised quantiles, we introduce the notion of kernel quantile embeddings (KQEs). We then use KQEs to construct a family of distances that: (i) are probability metrics under weaker kernel conditions than MMD; (ii) recover a kernelised form of the sliced Wasserstein distance; and (iii) can be efficiently estimated with near-linear cost. Through hypothesis testing, we show that these distances offer a competitive alternative to MMD and its fast approximations.

A Dictionary of Closed-Form Kernel Mean Embeddings

Kernel mean embeddings -- integrals of a kernel with respect to a probability distribution -- are essential in Bayesian quadrature, but also widely used in other computational tools for numerical integration or for statistical inference based on the maximum mean discrepancy. These methods often require, or are enhanced by, the availability of a closed-form expression for the kernel mean embedding. However, deriving such expressions can be challenging, limiting the applicability of kernel-based techniques when practitioners do not have access to a closed-form embedding. This paper addresses this limitation by providing a comprehensive dictionary of known kernel mean embeddings, along with practical tools for deriving new embeddings from known ones. We also provide a Python library that includes minimal implementations of the embeddings.

Nested Expectations with Kernel Quadrature

This paper considers the challenging computational task of estimating nested expectations. Existing algorithms, such as nested Monte Carlo or multilevel Monte Carlo, are known to be consistent but require a large number of samples at both inner and outer levels to converge. Instead, we propose a novel estimator consisting of nested kernel quadrature estimators and we prove that it has a faster convergence rate than all baseline methods when the integrands have sufficient smoothness. We then demonstrate empirically that our proposed method does indeed require fewer samples to estimate nested expectations on real-world applications including Bayesian optimisation, option pricing, and health economics.

Robust and Conjugate Spatio-Temporal Gaussian Processes

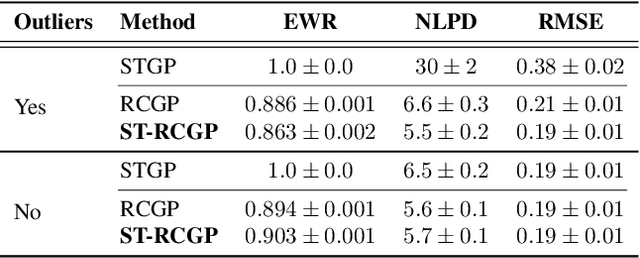
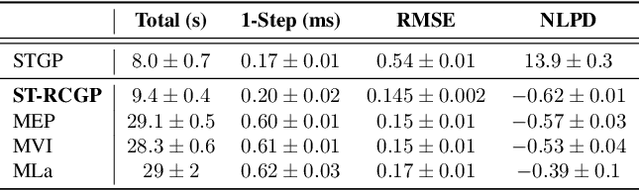
State-space formulations allow for Gaussian process (GP) regression with linear-in-time computational cost in spatio-temporal settings, but performance typically suffers in the presence of outliers. In this paper, we adapt and specialise the robust and conjugate GP (RCGP) framework of Altamirano et al. (2024) to the spatio-temporal setting. In doing so, we obtain an outlier-robust spatio-temporal GP with a computational cost comparable to classical spatio-temporal GPs. We also overcome the three main drawbacks of RCGPs: their unreliable performance when the prior mean is chosen poorly, their lack of reliable uncertainty quantification, and the need to carefully select a hyperparameter by hand. We study our method extensively in finance and weather forecasting applications, demonstrating that it provides a reliable approach to spatio-temporal modelling in the presence of outliers.

Cost-aware Simulation-based Inference

Simulation-based inference (SBI) is the preferred framework for estimating parameters of intractable models in science and engineering. A significant challenge in this context is the large computational cost of simulating data from complex models, and the fact that this cost often depends on parameter values. We therefore propose \textit{cost-aware SBI methods} which can significantly reduce the cost of existing sampling-based SBI methods, such as neural SBI and approximate Bayesian computation. This is achieved through a combination of rejection and self-normalised importance sampling, which significantly reduces the number of expensive simulations needed. Our approach is studied extensively on models from epidemiology to telecommunications engineering, where we obtain significant reductions in the overall cost of inference.

On the Robustness of Kernel Goodness-of-Fit Tests

Goodness-of-fit testing is often criticized for its lack of practical relevance; since ``all models are wrong'', the null hypothesis that the data conform to our model is ultimately always rejected when the sample size is large enough. Despite this, probabilistic models are still used extensively, raising the more pertinent question of whether the model is good enough for a specific task. This question can be formalized as a robust goodness-of-fit testing problem by asking whether the data were generated by a distribution corresponding to our model up to some mild perturbation. In this paper, we show that existing kernel goodness-of-fit tests are not robust according to common notions of robustness including qualitative and quantitative robustness. We also show that robust techniques based on tilted kernels from the parameter estimation literature are not sufficient for ensuring both types of robustness in the context of goodness-of-fit testing. We therefore propose the first robust kernel goodness-of-fit test which resolves this open problem using kernel Stein discrepancy balls, which encompass perturbation models such as Huber contamination models and density uncertainty bands.

Conditional Bayesian Quadrature

We propose a novel approach for estimating conditional or parametric expectations in the setting where obtaining samples or evaluating integrands is costly. Through the framework of probabilistic numerical methods (such as Bayesian quadrature), our novel approach allows to incorporates prior information about the integrands especially the prior smoothness knowledge about the integrands and the conditional expectation. As a result, our approach provides a way of quantifying uncertainty and leads to a fast convergence rate, which is confirmed both theoretically and empirically on challenging tasks in Bayesian sensitivity analysis, computational finance and decision making under uncertainty.

Outlier-robust Kalman Filtering through Generalised Bayes

We derive a novel, provably robust, and closed-form Bayesian update rule for online filtering in state-space models in the presence of outliers and misspecified measurement models. Our method combines generalised Bayesian inference with filtering methods such as the extended and ensemble Kalman filter. We use the former to show robustness and the latter to ensure computational efficiency in the case of nonlinear models. Our method matches or outperforms other robust filtering methods (such as those based on variational Bayes) at a much lower computational cost. We show this empirically on a range of filtering problems with outlier measurements, such as object tracking, state estimation in high-dimensional chaotic systems, and online learning of neural networks.