Invariant Feature Extraction Through Conditional Independence and the Optimal Transport Barycenter Problem: the Gaussian case

A methodology is developed to extract $d$ invariant features $W=f(X)$ that predict a response variable $Y$ without being confounded by variables $Z$ that may influence both $X$ and $Y$. The methodology's main ingredient is the penalization of any statistical dependence between $W$ and $Z$ conditioned on $Y$, replaced by the more readily implementable plain independence between $W$ and the random variable $Z_Y = T(Z,Y)$ that solves the [Monge] Optimal Transport Barycenter Problem for $Z\mid Y$. In the Gaussian case considered in this article, the two statements are equivalent. When the true confounders $Z$ are unknown, other measurable contextual variables $S$ can be used as surrogates, a replacement that involves no relaxation in the Gaussian case if the covariance matrix $Σ_{ZS}$ has full range. The resulting linear feature extractor adopts a closed form in terms of the first $d$ eigenvectors of a known matrix. The procedure extends with little change to more general, non-Gaussian / non-linear cases.

Siamese networks for Poincaré embeddings and the reconstruction of evolutionary trees

We present a method for reconstructing evolutionary trees from high-dimensional data, with a specific application to bird song spectrograms. We address the challenge of inferring phylogenetic relationships from phenotypic traits, like vocalizations, without predefined acoustic properties. Our approach combines two main components: Poincar\'e embeddings for dimensionality reduction and distance computation, and the neighbor joining algorithm for tree reconstruction. Unlike previous work, we employ Siamese networks to learn embeddings from only leaf node samples of the latent tree. We demonstrate our method's effectiveness on both synthetic data and spectrograms from six species of finches.

Choosing the parameter of the Fermat distance: navigating geometry and noise

The Fermat distance has been recently established as a useful tool for machine learning tasks when a natural distance is not directly available to the practitioner or to improve the results given by Euclidean distances by exploding the geometrical and statistical properties of the dataset. This distance depends on a parameter $\alpha$ that greatly impacts the performance of subsequent tasks. Ideally, the value of $\alpha$ should be large enough to navigate the geometric intricacies inherent to the problem. At the same, it should remain restrained enough to sidestep any deleterious ramifications stemming from noise during the process of distance estimation. We study both theoretically and through simulations how to select this parameter.

Intrinsic persistent homology via density-based metric learning

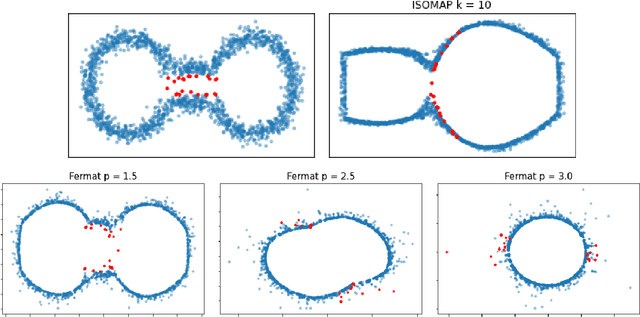
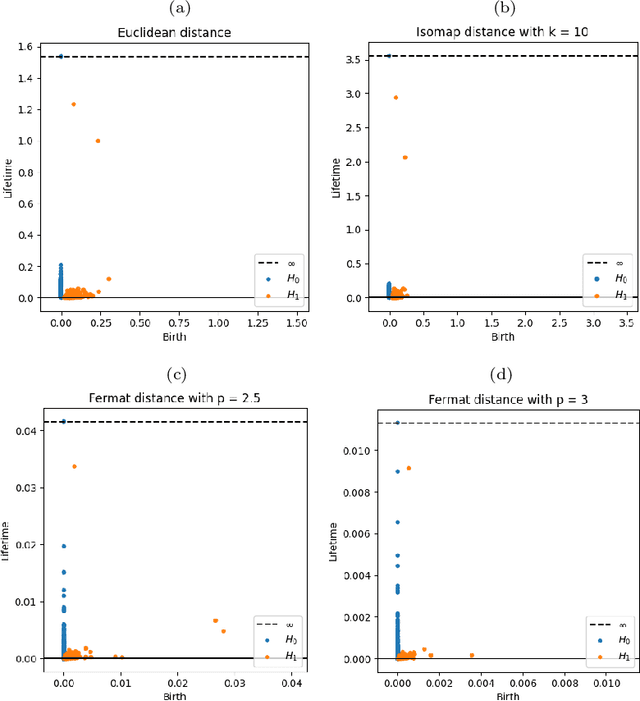
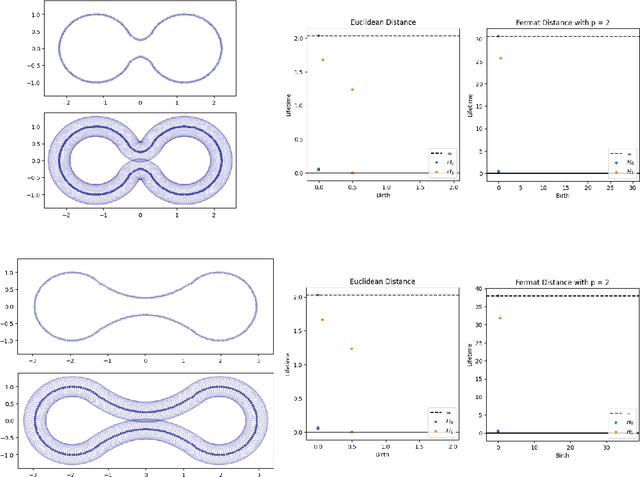
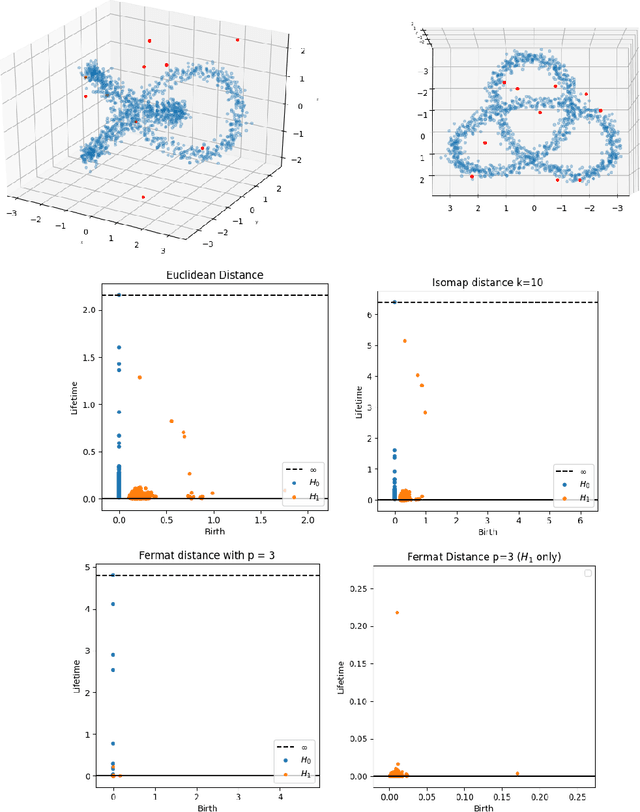
We address the problem of estimating intrinsic distances in a manifold from a finite sample. We prove that the metric space defined by the sample endowed with a computable metric known as sample Fermat distance converges a.s. in the sense of Gromov-Hausdorff. The limiting object is the manifold itself endowed with the population Fermat distance, an intrinsic metric that accounts for both the geometry of the manifold and the density that produces the sample. This result is applied to obtain sample persistence diagrams that converge towards an intrinsic persistence diagram. We show that this method outperforms more standard approaches based on Euclidean norm with theoretical results and computational experiments.