From Words to Amino Acids: Does the Curse of Depth Persist?

Protein language models (PLMs) have become widely adopted as general-purpose models, demonstrating strong performance in protein engineering and de novo design. Like large language models (LLMs), they are typically trained as deep transformers with next-token or masked-token prediction objectives on massive sequence corpora and are scaled by increasing model depth. Recent work on autoregressive LLMs has identified the Curse of Depth: later layers contribute little to the final output predictions. These findings naturally raise the question of whether a similar depth inefficiency also appears in PLMs, where many widely used models are not autoregressive, and some are multimodal, accepting both protein sequence and structure as input. In this work, we present a depth analysis of six popular PLMs across model families and scales, spanning three training objectives, namely autoregressive, masked, and diffusion, and quantify how layer contributions evolve with depth using a unified set of probing- and perturbation-based measurements. Across all models, we observe consistent depth-dependent patterns that extend prior findings on LLMs: later layers depend less on earlier computations and mainly refine the final output distribution, and these effects are increasingly pronounced in deeper models. Taken together, our results suggest that PLMs exhibit a form of depth inefficiency, motivating future work on more depth-efficient architectures and training methods.

From Growing to Looping: A Unified View of Iterative Computation in LLMs

Looping, reusing a block of layers across depth, and depth growing, training shallow-to-deep models by duplicating middle layers, have both been linked to stronger reasoning, but their relationship remains unclear. We provide a mechanistic unification: looped and depth-grown models exhibit convergent depth-wise signatures, including increased reliance on late layers and recurring patterns aligned with the looped or grown block. These shared signatures support the view that their gains stem from a common form of iterative computation. Building on this connection, we show that the two techniques are adaptable and composable: applying inference-time looping to the middle blocks of a depth-grown model improves accuracy on some reasoning primitives by up to $2\times$, despite the model never being trained to loop. Both approaches also adapt better than the baseline when given more in-context examples or additional supervised fine-tuning data. Additionally, depth-grown models achieve the largest reasoning gains when using higher-quality, math-heavy cooldown mixtures, which can be further boosted by adapting a middle block to loop. Overall, our results position depth growth and looping as complementary, practical methods for inducing and scaling iterative computation to improve reasoning.

Do Depth-Grown Models Overcome the Curse of Depth? An In-Depth Analysis

Gradually growing the depth of Transformers during training can not only reduce training cost but also lead to improved reasoning performance, as shown by MIDAS (Saunshi et al., 2024). Thus far, however, a mechanistic understanding of these gains has been missing. In this work, we establish a connection to recent work showing that layers in the second half of non-grown, pre-layernorm Transformers contribute much less to the final output distribution than those in the first half - also known as the Curse of Depth (Sun et al., 2025, Csordás et al., 2025). Using depth-wise analyses, we demonstrate that growth via gradual middle stacking yields more effective utilization of model depth, alters the residual stream structure, and facilitates the formation of permutable computational blocks. In addition, we propose a lightweight modification of MIDAS that yields further improvements in downstream reasoning benchmarks. Overall, this work highlights how the gradual growth of model depth can lead to the formation of distinct computational circuits and overcome the limited depth utilization seen in standard non-grown models.

Minimum-Excess-Work Guidance

We propose a regularization framework inspired by thermodynamic work for guiding pre-trained probability flow generative models (e.g., continuous normalizing flows or diffusion models) by minimizing excess work, a concept rooted in statistical mechanics and with strong conceptual connections to optimal transport. Our approach enables efficient guidance in sparse-data regimes common to scientific applications, where only limited target samples or partial density constraints are available. We introduce two strategies: Path Guidance for sampling rare transition states by concentrating probability mass on user-defined subsets, and Observable Guidance for aligning generated distributions with experimental observables while preserving entropy. We demonstrate the framework's versatility on a coarse-grained protein model, guiding it to sample transition configurations between folded/unfolded states and correct systematic biases using experimental data. The method bridges thermodynamic principles with modern generative architectures, offering a principled, efficient, and physics-inspired alternative to standard fine-tuning in data-scarce domains. Empirical results highlight improved sample efficiency and bias reduction, underscoring its applicability to molecular simulations and beyond.

Doubly Robust Structure Identification from Temporal Data

Learning the causes of time-series data is a fundamental task in many applications, spanning from finance to earth sciences or bio-medical applications. Common approaches for this task are based on vector auto-regression, and they do not take into account unknown confounding between potential causes. However, in settings with many potential causes and noisy data, these approaches may be substantially biased. Furthermore, potential causes may be correlated in practical applications. Moreover, existing algorithms often do not work with cyclic data. To address these challenges, we propose a new doubly robust method for Structure Identification from Temporal Data ( SITD ). We provide theoretical guarantees, showing that our method asymptotically recovers the true underlying causal structure. Our analysis extends to cases where the potential causes have cycles and they may be confounded. We further perform extensive experiments to showcase the superior performance of our method.

SLEIPNIR: Deterministic and Provably Accurate Feature Expansion for Gaussian Process Regression with Derivatives

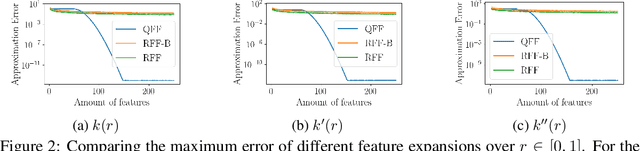
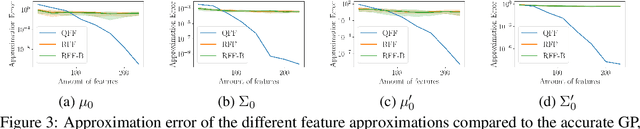
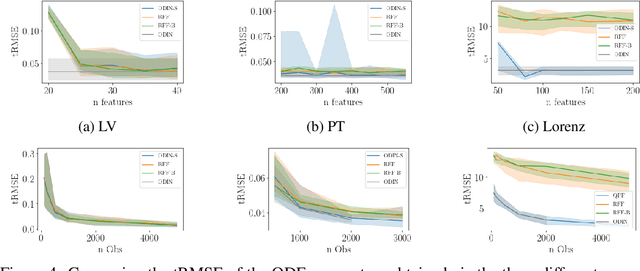
Gaussian processes are an important regression tool with excellent analytic properties which allow for direct integration of derivative observations. However, vanilla GP methods scale cubically in the amount of observations. In this work, we propose a novel approach for scaling GP regression with derivatives based on quadrature Fourier features. We then prove deterministic, non-asymptotic and exponentially fast decaying error bounds which apply for both the approximated kernel as well as the approximated posterior. To furthermore illustrate the practical applicability of our method, we then apply it to ODIN, a recently developed algorithm for ODE parameter inference. In an extensive experiments section, all results are empirically validated, demonstrating the speed, accuracy, and practical applicability of this approach.