Emergent temporal abstractions in autoregressive models enable hierarchical reinforcement learning

Large-scale autoregressive models pretrained on next-token prediction and finetuned with reinforcement learning (RL) have achieved unprecedented success on many problem domains. During RL, these models explore by generating new outputs, one token at a time. However, sampling actions token-by-token can result in highly inefficient learning, particularly when rewards are sparse. Here, we show that it is possible to overcome this problem by acting and exploring within the internal representations of an autoregressive model. Specifically, to discover temporally-abstract actions, we introduce a higher-order, non-causal sequence model whose outputs control the residual stream activations of a base autoregressive model. On grid world and MuJoCo-based tasks with hierarchical structure, we find that the higher-order model learns to compress long activation sequence chunks onto internal controllers. Critically, each controller executes a sequence of behaviorally meaningful actions that unfold over long timescales and are accompanied with a learned termination condition, such that composing multiple controllers over time leads to efficient exploration on novel tasks. We show that direct internal controller reinforcement, a process we term "internal RL", enables learning from sparse rewards in cases where standard RL finetuning fails. Our results demonstrate the benefits of latent action generation and reinforcement in autoregressive models, suggesting internal RL as a promising avenue for realizing hierarchical RL within foundation models.

Best Practices For Empirical Meta-Algorithmic Research: Guidelines from the COSEAL Research Network

Empirical research on meta-algorithmics, such as algorithm selection, configuration, and scheduling, often relies on extensive and thus computationally expensive experiments. With the large degree of freedom we have over our experimental setup and design comes a plethora of possible error sources that threaten the scalability and validity of our scientific insights. Best practices for meta-algorithmic research exist, but they are scattered between different publications and fields, and continue to evolve separately from each other. In this report, we collect good practices for empirical meta-algorithmic research across the subfields of the COSEAL community, encompassing the entire experimental cycle: from formulating research questions and selecting an experimental design, to executing experiments, and ultimately, analyzing and presenting results impartially. It establishes the current state-of-the-art practices within meta-algorithmic research and serves as a guideline to both new researchers and practitioners in meta-algorithmic fields.

Do Depth-Grown Models Overcome the Curse of Depth? An In-Depth Analysis

Gradually growing the depth of Transformers during training can not only reduce training cost but also lead to improved reasoning performance, as shown by MIDAS (Saunshi et al., 2024). Thus far, however, a mechanistic understanding of these gains has been missing. In this work, we establish a connection to recent work showing that layers in the second half of non-grown, pre-layernorm Transformers contribute much less to the final output distribution than those in the first half - also known as the Curse of Depth (Sun et al., 2025, Csordás et al., 2025). Using depth-wise analyses, we demonstrate that growth via gradual middle stacking yields more effective utilization of model depth, alters the residual stream structure, and facilitates the formation of permutable computational blocks. In addition, we propose a lightweight modification of MIDAS that yields further improvements in downstream reasoning benchmarks. Overall, this work highlights how the gradual growth of model depth can lead to the formation of distinct computational circuits and overcome the limited depth utilization seen in standard non-grown models.

MesaNet: Sequence Modeling by Locally Optimal Test-Time Training

Sequence modeling is currently dominated by causal transformer architectures that use softmax self-attention. Although widely adopted, transformers require scaling memory and compute linearly during inference. A recent stream of work linearized the softmax operation, resulting in powerful recurrent neural network (RNN) models with constant memory and compute costs such as DeltaNet, Mamba or xLSTM. These models can be unified by noting that their recurrent layer dynamics can all be derived from an in-context regression objective, approximately optimized through an online learning rule. Here, we join this line of work and introduce a numerically stable, chunkwise parallelizable version of the recently proposed Mesa layer (von Oswald et al., 2024), and study it in language modeling at the billion-parameter scale. This layer again stems from an in-context loss, but which is now minimized to optimality at every time point using a fast conjugate gradient solver. Through an extensive suite of experiments, we show that optimal test-time training enables reaching lower language modeling perplexity and higher downstream benchmark performance than previous RNNs, especially on tasks requiring long context understanding. This performance gain comes at the cost of additional flops spent during inference time. Our results are therefore intriguingly related to recent trends of increasing test-time compute to improve performance -- here by spending compute to solve sequential optimization problems within the neural network itself.

Composable Function-preserving Expansions for Transformer Architectures

Training state-of-the-art neural networks requires a high cost in terms of compute and time. Model scale is recognized to be a critical factor to achieve and improve the state-of-the-art. Increasing the scale of a neural network normally requires restarting from scratch by randomly initializing all the parameters of the model, as this implies a change of architecture's parameters that does not allow for a straightforward transfer of knowledge from smaller size models. In this work, we propose six composable transformations to incrementally increase the size of transformer-based neural networks while preserving functionality, allowing to expand the capacity of the model as needed. We provide proof of exact function preservation under minimal initialization constraints for each transformation. The proposed methods may enable efficient training pipelines for larger and more powerful models by progressively expanding the architecture throughout training.

Architectural Optimization over Subgroups for Equivariant Neural Networks

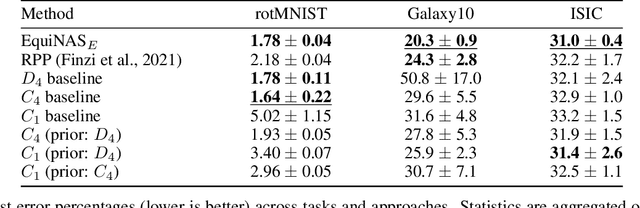
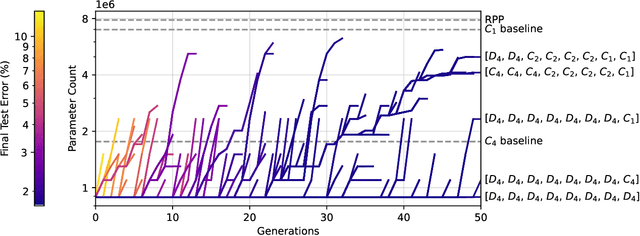
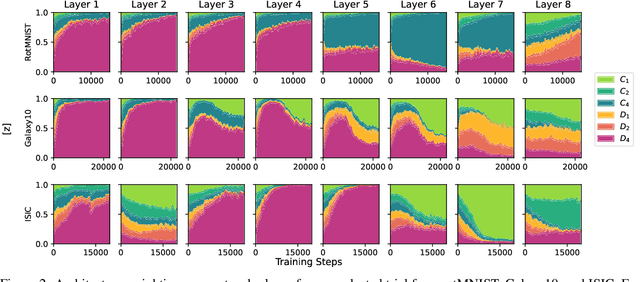
Incorporating equivariance to symmetry groups as a constraint during neural network training can improve performance and generalization for tasks exhibiting those symmetries, but such symmetries are often not perfectly nor explicitly present. This motivates algorithmically optimizing the architectural constraints imposed by equivariance. We propose the equivariance relaxation morphism, which preserves functionality while reparameterizing a group equivariant layer to operate with equivariance constraints on a subgroup, as well as the $[G]$-mixed equivariant layer, which mixes layers constrained to different groups to enable within-layer equivariance optimization. We further present evolutionary and differentiable neural architecture search (NAS) algorithms that utilize these mechanisms respectively for equivariance-aware architectural optimization. Experiments across a variety of datasets show the benefit of dynamically constrained equivariance to find effective architectures with approximate equivariance.

When, where, and how to add new neurons to ANNs

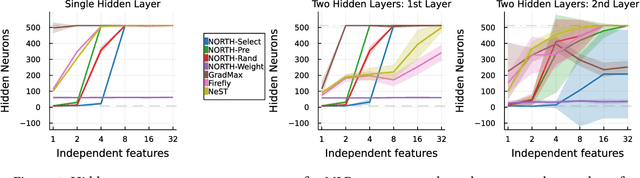
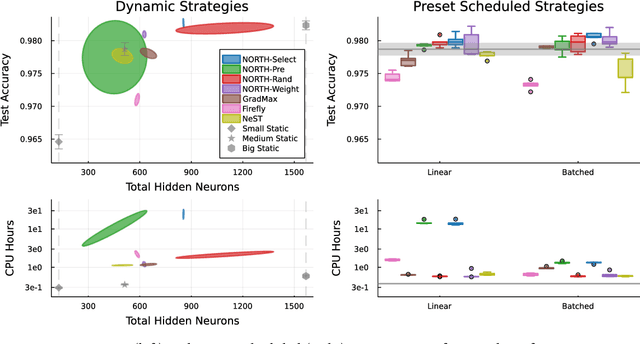
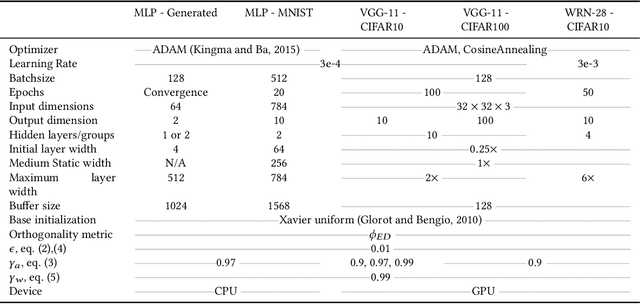
Neurogenesis in ANNs is an understudied and difficult problem, even compared to other forms of structural learning like pruning. By decomposing it into triggers and initializations, we introduce a framework for studying the various facets of neurogenesis: when, where, and how to add neurons during the learning process. We present the Neural Orthogonality (NORTH*) suite of neurogenesis strategies, combining layer-wise triggers and initializations based on the orthogonality of activations or weights to dynamically grow performant networks that converge to an efficient size. We evaluate our contributions against other recent neurogenesis works with MLPs.

On Constrained Optimization in Differentiable Neural Architecture Search

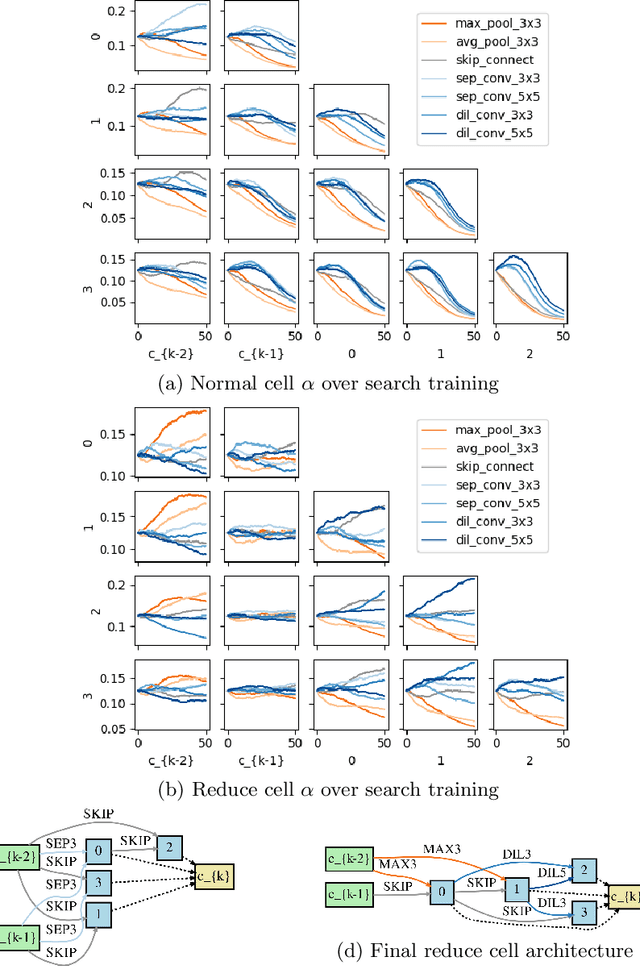
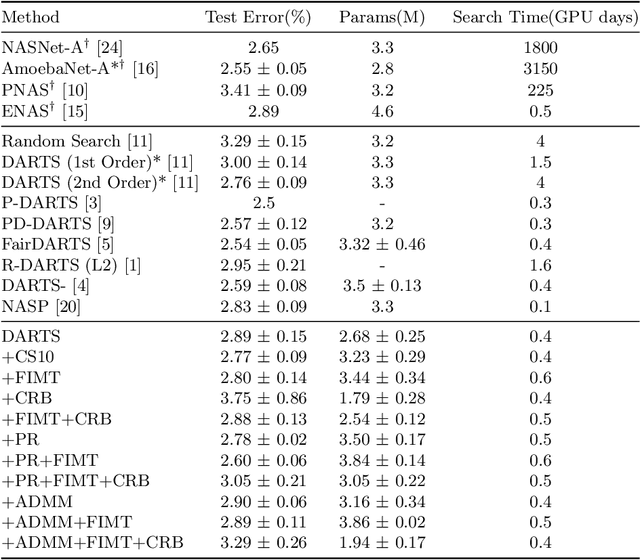
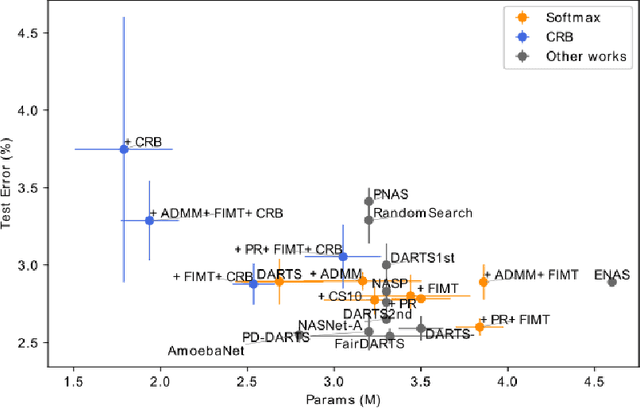
Differentiable Architecture Search (DARTS) is a recently proposed neural architecture search (NAS) method based on a differentiable relaxation. Due to its success, numerous variants analyzing and improving parts of the DARTS framework have recently been proposed. By considering the problem as a constrained bilevel optimization, we propose and analyze three improvements to architectural weight competition, update scheduling, and regularization towards discretization. First, we introduce a new approach to the activation of architecture weights, which prevents confounding competition within an edge and allows for fair comparison across edges to aid in discretization. Next, we propose a dynamic schedule based on per-minibatch network information to make architecture updates more informed. Finally, we consider two regularizations, based on proximity to discretization and the Alternating Directions Method of Multipliers (ADMM) algorithm, to promote early discretization. Our results show that this new activation scheme reduces final architecture size and the regularizations improve reliability in search results while maintaining comparable performance to state-of-the-art in NAS, especially when used with our new dynamic informed schedule.