Posterior Covariance Structures in Gaussian Processes

In this paper, we present a comprehensive analysis of the posterior covariance field in Gaussian processes, with applications to the posterior covariance matrix. The analysis is based on the Gaussian prior covariance but the approach also applies to other covariance kernels. Our geometric analysis reveals how the Gaussian kernel's bandwidth parameter and the spatial distribution of the observations influence the posterior covariance as well as the corresponding covariance matrix, enabling straightforward identification of areas with high or low covariance in magnitude. Drawing inspiration from the a posteriori error estimation techniques in adaptive finite element methods, we also propose several estimators to efficiently measure the absolute posterior covariance field, which can be used for efficient covariance matrix approximation and preconditioning. We conduct a wide range of experiments to illustrate our theoretical findings and their practical applications.

Efficient Two-Stage Gaussian Process Regression Via Automatic Kernel Search and Subsampling

Gaussian Process Regression (GPR) is widely used in statistics and machine learning for prediction tasks requiring uncertainty measures. Its efficacy depends on the appropriate specification of the mean function, covariance kernel function, and associated hyperparameters. Severe misspecifications can lead to inaccurate results and problematic consequences, especially in safety-critical applications. However, a systematic approach to handle these misspecifications is lacking in the literature. In this work, we propose a general framework to address these issues. Firstly, we introduce a flexible two-stage GPR framework that separates mean prediction and uncertainty quantification (UQ) to prevent mean misspecification, which can introduce bias into the model. Secondly, kernel function misspecification is addressed through a novel automatic kernel search algorithm, supported by theoretical analysis, that selects the optimal kernel from a candidate set. Additionally, we propose a subsampling-based warm-start strategy for hyperparameter initialization to improve efficiency and avoid hyperparameter misspecification. With much lower computational cost, our subsampling-based strategy can yield competitive or better performance than training exclusively on the full dataset. Combining all these components, we recommend two GPR methods-exact and scalable-designed to match available computational resources and specific UQ requirements. Extensive evaluation on real-world datasets, including UCI benchmarks and a safety-critical medical case study, demonstrates the robustness and precision of our methods.

Learning to Relax: Setting Solver Parameters Across a Sequence of Linear System Instances

Solving a linear system $Ax=b$ is a fundamental scientific computing primitive for which numerous solvers and preconditioners have been developed. These come with parameters whose optimal values depend on the system being solved and are often impossible or too expensive to identify; thus in practice sub-optimal heuristics are used. We consider the common setting in which many related linear systems need to be solved, e.g. during a single numerical simulation. In this scenario, can we sequentially choose parameters that attain a near-optimal overall number of iterations, without extra matrix computations? We answer in the affirmative for Successive Over-Relaxation (SOR), a standard solver whose parameter $\omega$ has a strong impact on its runtime. For this method, we prove that a bandit online learning algorithm -- using only the number of iterations as feedback -- can select parameters for a sequence of instances such that the overall cost approaches that of the best fixed $\omega$ as the sequence length increases. Furthermore, when given additional structural information, we show that a contextual bandit method asymptotically achieves the performance of the instance-optimal policy, which selects the best $\omega$ for each instance. Our work provides the first learning-theoretic treatment of high-precision linear system solvers and the first end-to-end guarantees for data-driven scientific computing, demonstrating theoretically the potential to speed up numerical methods using well-understood learning algorithms.

Data-Driven Linear Complexity Low-Rank Approximation of General Kernel Matrices: A Geometric Approach

A general, {\em rectangular} kernel matrix may be defined as $K_{ij} = \kappa(x_i,y_j)$ where $\kappa(x,y)$ is a kernel function and where $X=\{x_i\}_{i=1}^m$ and $Y=\{y_i\}_{i=1}^n$ are two sets of points. In this paper, we seek a low-rank approximation to a kernel matrix where the sets of points $X$ and $Y$ are large and are not well-separated (e.g., the points in $X$ and $Y$ may be ``intermingled''). Such rectangular kernel matrices may arise, for example, in Gaussian process regression where $X$ corresponds to the training data and $Y$ corresponds to the test data. In this case, the points are often high-dimensional. Since the point sets are large, we must exploit the fact that the matrix arises from a kernel function, and avoid forming the matrix, and thus ruling out most algebraic techniques. In particular, we seek methods that can scale linearly, i.e., with computational complexity $O(m)$ or $O(n)$ for a fixed accuracy or rank. The main idea in this paper is to {\em geometrically} select appropriate subsets of points to construct a low rank approximation. An analysis in this paper guides how this selection should be performed.

Integrating Deep Learning in Domain Sciences at Exascale

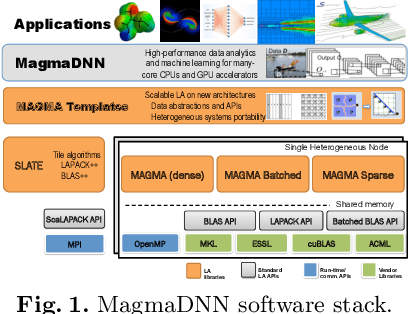
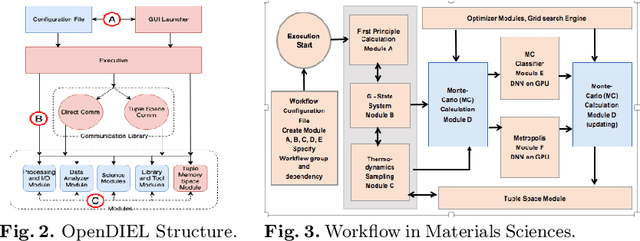
This paper presents some of the current challenges in designing deep learning artificial intelligence (AI) and integrating it with traditional high-performance computing (HPC) simulations. We evaluate existing packages for their ability to run deep learning models and applications on large-scale HPC systems efficiently, identify challenges, and propose new asynchronous parallelization and optimization techniques for current large-scale heterogeneous systems and upcoming exascale systems. These developments, along with existing HPC AI software capabilities, have been integrated into MagmaDNN, an open-source HPC deep learning framework. Many deep learning frameworks are targeted at data scientists and fall short in providing quality integration into existing HPC workflows. This paper discusses the necessities of an HPC deep learning framework and how those needs can be provided (e.g., as in MagmaDNN) through a deep integration with existing HPC libraries, such as MAGMA and its modular memory management, MPI, CuBLAS, CuDNN, MKL, and HIP. Advancements are also illustrated through the use of algorithmic enhancements in reduced- and mixed-precision, as well as asynchronous optimization methods. Finally, we present illustrations and potential solutions for enhancing traditional compute- and data-intensive applications at ORNL and UTK with AI. The approaches and future challenges are illustrated in materials science, imaging, and climate applications.

Knowledge Representation Issues in Semantic Graphs for Relationship Detection

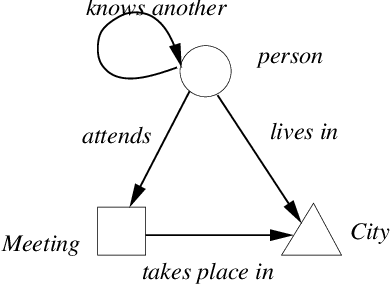
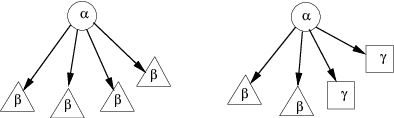
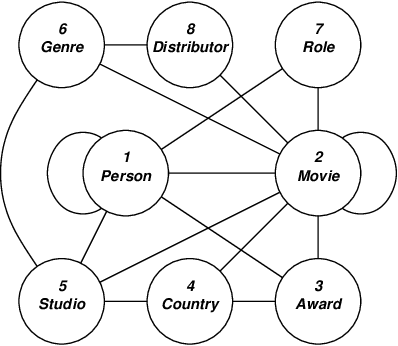
An important task for Homeland Security is the prediction of threat vulnerabilities, such as through the detection of relationships between seemingly disjoint entities. A structure used for this task is a "semantic graph", also known as a "relational data graph" or an "attributed relational graph". These graphs encode relationships as "typed" links between a pair of "typed" nodes. Indeed, semantic graphs are very similar to semantic networks used in AI. The node and link types are related through an ontology graph (also known as a schema). Furthermore, each node has a set of attributes associated with it (e.g., "age" may be an attribute of a node of type "person"). Unfortunately, the selection of types and attributes for both nodes and links depends on human expertise and is somewhat subjective and even arbitrary. This subjectiveness introduces biases into any algorithm that operates on semantic graphs. Here, we raise some knowledge representation issues for semantic graphs and provide some possible solutions using recently developed ideas in the field of complex networks. In particular, we use the concept of transitivity to evaluate the relevance of individual links in the semantic graph for detecting relationships. We also propose new statistical measures for semantic graphs and illustrate these semantic measures on graphs constructed from movies and terrorism data.