Posterior Covariance Structures in Gaussian Processes

In this paper, we present a comprehensive analysis of the posterior covariance field in Gaussian processes, with applications to the posterior covariance matrix. The analysis is based on the Gaussian prior covariance but the approach also applies to other covariance kernels. Our geometric analysis reveals how the Gaussian kernel's bandwidth parameter and the spatial distribution of the observations influence the posterior covariance as well as the corresponding covariance matrix, enabling straightforward identification of areas with high or low covariance in magnitude. Drawing inspiration from the a posteriori error estimation techniques in adaptive finite element methods, we also propose several estimators to efficiently measure the absolute posterior covariance field, which can be used for efficient covariance matrix approximation and preconditioning. We conduct a wide range of experiments to illustrate our theoretical findings and their practical applications.

Data-Driven Linear Complexity Low-Rank Approximation of General Kernel Matrices: A Geometric Approach

A general, {\em rectangular} kernel matrix may be defined as $K_{ij} = \kappa(x_i,y_j)$ where $\kappa(x,y)$ is a kernel function and where $X=\{x_i\}_{i=1}^m$ and $Y=\{y_i\}_{i=1}^n$ are two sets of points. In this paper, we seek a low-rank approximation to a kernel matrix where the sets of points $X$ and $Y$ are large and are not well-separated (e.g., the points in $X$ and $Y$ may be ``intermingled''). Such rectangular kernel matrices may arise, for example, in Gaussian process regression where $X$ corresponds to the training data and $Y$ corresponds to the test data. In this case, the points are often high-dimensional. Since the point sets are large, we must exploit the fact that the matrix arises from a kernel function, and avoid forming the matrix, and thus ruling out most algebraic techniques. In particular, we seek methods that can scale linearly, i.e., with computational complexity $O(m)$ or $O(n)$ for a fixed accuracy or rank. The main idea in this paper is to {\em geometrically} select appropriate subsets of points to construct a low rank approximation. An analysis in this paper guides how this selection should be performed.

AUTM Flow: Atomic Unrestricted Time Machine for Monotonic Normalizing Flows

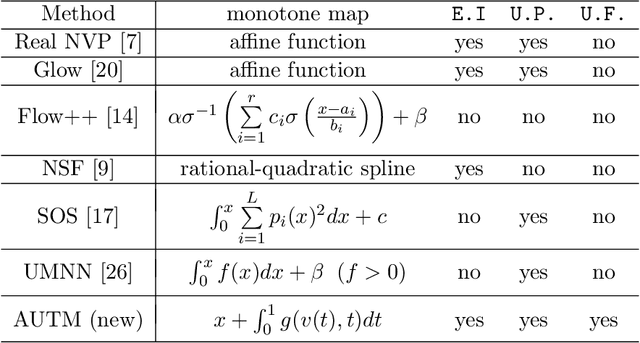
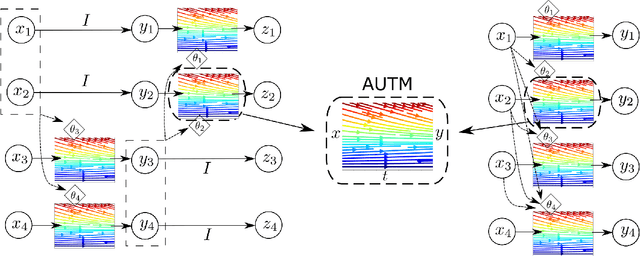
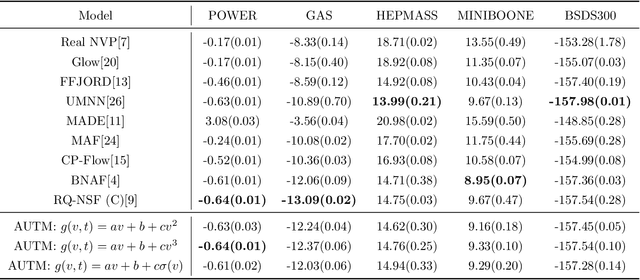
Nonlinear monotone transformations are used extensively in normalizing flows to construct invertible triangular mappings from simple distributions to complex ones. In existing literature, monotonicity is usually enforced by restricting function classes or model parameters and the inverse transformation is often approximated by root-finding algorithms as a closed-form inverse is unavailable. In this paper, we introduce a new integral-based approach termed "Atomic Unrestricted Time Machine (AUTM)", equipped with unrestricted integrands and easy-to-compute explicit inverse. AUTM offers a versatile and efficient way to the design of normalizing flows with explicit inverse and unrestricted function classes or parameters. Theoretically, we present a constructive proof that AUTM is universal: all monotonic normalizing flows can be viewed as limits of AUTM flows. We provide a concrete example to show how to approximate any given monotonic normalizing flow using AUTM flows with guaranteed convergence. The result implies that AUTM can be used to transform an existing flow into a new one equipped with explicit inverse and unrestricted parameters. The performance of the new approach is evaluated on high dimensional density estimation, variational inference and image generation. Experiments demonstrate superior speed and memory efficiency of AUTM.