GPS++: An Optimised Hybrid MPNN/Transformer for Molecular Property Prediction

This technical report presents GPS++, the first-place solution to the Open Graph Benchmark Large-Scale Challenge (OGB-LSC 2022) for the PCQM4Mv2 molecular property prediction task. Our approach implements several key principles from the prior literature. At its core our GPS++ method is a hybrid MPNN/Transformer model that incorporates 3D atom positions and an auxiliary denoising task. The effectiveness of GPS++ is demonstrated by achieving 0.0719 mean absolute error on the independent test-challenge PCQM4Mv2 split. Thanks to Graphcore IPU acceleration, GPS++ scales to deep architectures (16 layers), training at 3 minutes per epoch, and large ensemble (112 models), completing the final predictions in 1 hour 32 minutes, well under the 4 hour inference budget allocated. Our implementation is publicly available at: https://github.com/graphcore/ogb-lsc-pcqm4mv2.

Long Range Graph Benchmark

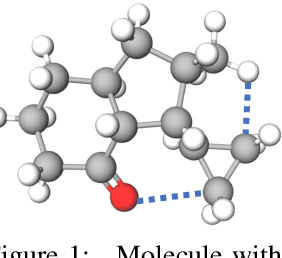
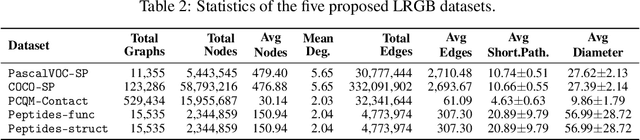
Graph Neural Networks (GNNs) that are based on the message passing (MP) paradigm exchange information between 1-hop neighbors to build node representations at each layer. In principle, such networks are not able to capture long-range interactions (LRI) that may be desired or necessary for learning a given task on graphs. Recently, there has been an increasing interest in development of Transformer-based methods for graphs that can consider full node connectivity beyond the original sparse structure, thus enabling the modeling of LRI. However, MP-GNNs that simply rely on 1-hop message passing often fare better in several existing graph benchmarks when combined with positional feature representations, among other innovations, hence limiting the perceived utility and ranking of Transformer-like architectures. Here, we present the Long Range Graph Benchmark (LRGB) with 5 graph learning datasets: PascalVOC-SP, COCO-SP, PCQM-Contact, Peptides-func and Peptides-struct that arguably require LRI reasoning to achieve strong performance in a given task. We benchmark both baseline GNNs and Graph Transformer networks to verify that the models which capture long-range dependencies perform significantly better on these tasks. Therefore, these datasets are suitable for benchmarking and exploration of MP-GNNs and Graph Transformer architectures that are intended to capture LRI.

Recipe for a General, Powerful, Scalable Graph Transformer

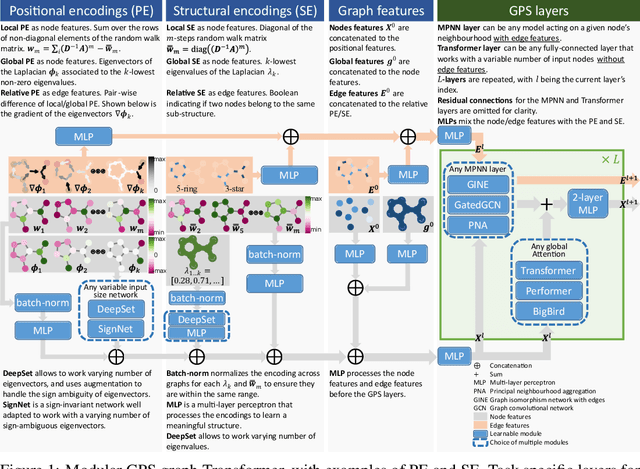
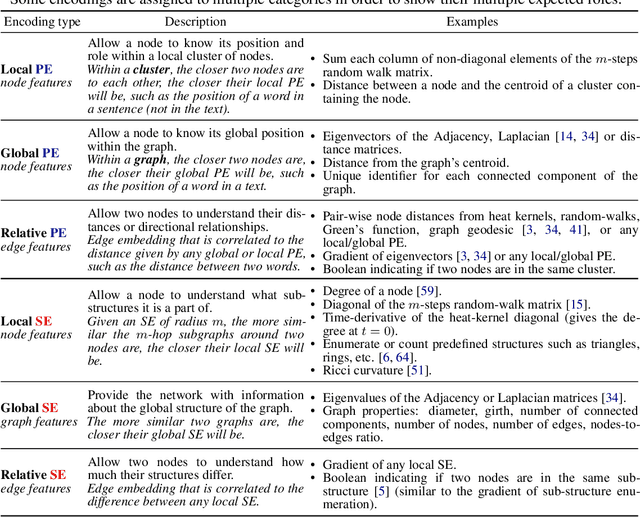
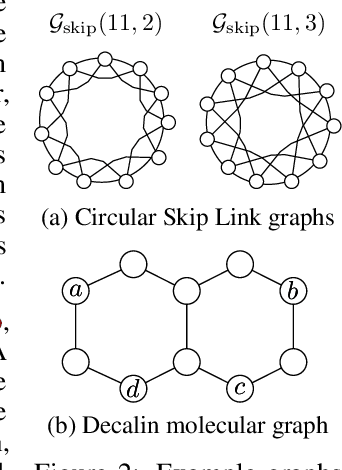
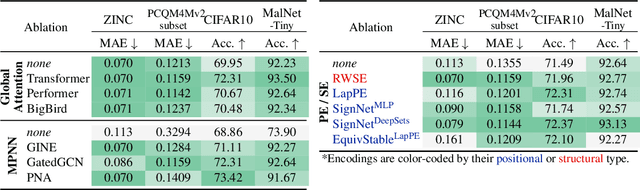
We propose a recipe on how to build a general, powerful, scalable (GPS) graph Transformer with linear complexity and state-of-the-art results on a diverse set of benchmarks. Graph Transformers (GTs) have gained popularity in the field of graph representation learning with a variety of recent publications but they lack a common foundation about what constitutes a good positional or structural encoding, and what differentiates them. In this paper, we summarize the different types of encodings with a clearer definition and categorize them as being $\textit{local}$, $\textit{global}$ or $\textit{relative}$. Further, GTs remain constrained to small graphs with few hundred nodes, and we propose the first architecture with a complexity linear to the number of nodes and edges $O(N+E)$ by decoupling the local real-edge aggregation from the fully-connected Transformer. We argue that this decoupling does not negatively affect the expressivity, with our architecture being a universal function approximator for graphs. Our GPS recipe consists of choosing 3 main ingredients: (i) positional/structural encoding, (ii) local message-passing mechanism, and (iii) global attention mechanism. We build and open-source a modular framework $\textit{GraphGPS}$ that supports multiple types of encodings and that provides efficiency and scalability both in small and large graphs. We test our architecture on 11 benchmarks and show very competitive results on all of them, show-casing the empirical benefits gained by the modularity and the combination of different strategies.

3D Infomax improves GNNs for Molecular Property Prediction

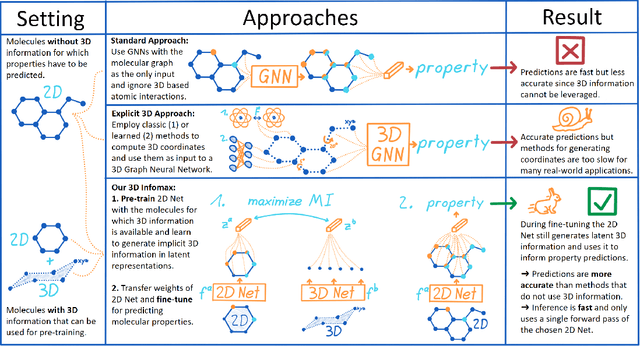
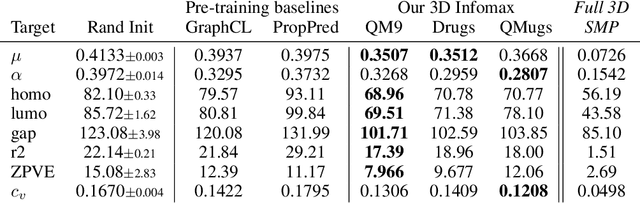
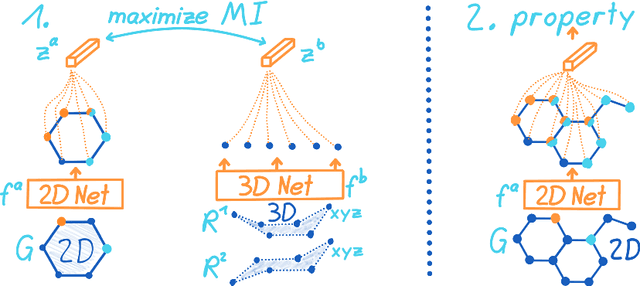
Molecular property prediction is one of the fastest-growing applications of deep learning with critical real-world impacts. Including 3D molecular structure as input to learned models their performance for many molecular tasks. However, this information is infeasible to compute at the scale required by several real-world applications. We propose pre-training a model to reason about the geometry of molecules given only their 2D molecular graphs. Using methods from self-supervised learning, we maximize the mutual information between 3D summary vectors and the representations of a Graph Neural Network (GNN) such that they contain latent 3D information. During fine-tuning on molecules with unknown geometry, the GNN still generates implicit 3D information and can use it to improve downstream tasks. We show that 3D pre-training provides significant improvements for a wide range of properties, such as a 22% average MAE reduction on eight quantum mechanical properties. Moreover, the learned representations can be effectively transferred between datasets in different molecular spaces.

Rethinking Graph Transformers with Spectral Attention

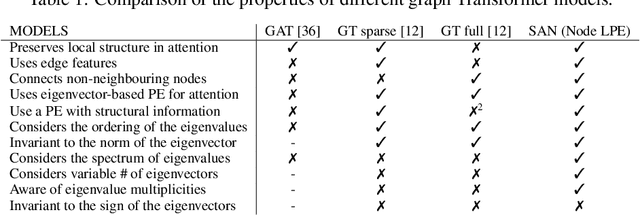
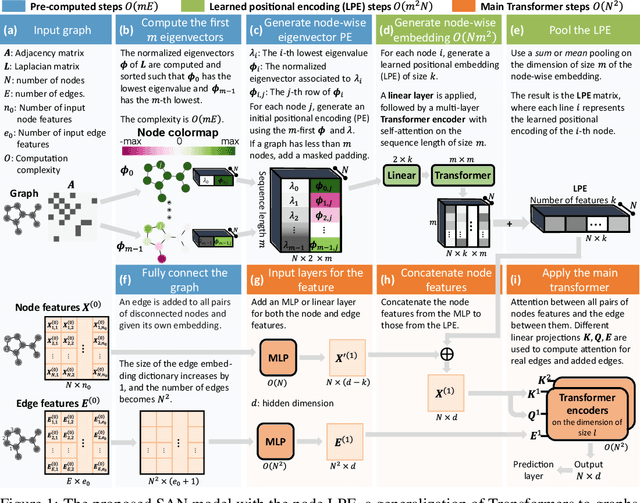
In recent years, the Transformer architecture has proven to be very successful in sequence processing, but its application to other data structures, such as graphs, has remained limited due to the difficulty of properly defining positions. Here, we present the $\textit{Spectral Attention Network}$ (SAN), which uses a learned positional encoding (LPE) that can take advantage of the full Laplacian spectrum to learn the position of each node in a given graph. This LPE is then added to the node features of the graph and passed to a fully-connected Transformer. By leveraging the full spectrum of the Laplacian, our model is theoretically powerful in distinguishing graphs, and can better detect similar sub-structures from their resonance. Further, by fully connecting the graph, the Transformer does not suffer from over-squashing, an information bottleneck of most GNNs, and enables better modeling of physical phenomenons such as heat transfer and electric interaction. When tested empirically on a set of 4 standard datasets, our model performs on par or better than state-of-the-art GNNs, and outperforms any attention-based model by a wide margin, becoming the first fully-connected architecture to perform well on graph benchmarks.

Directional Graph Networks

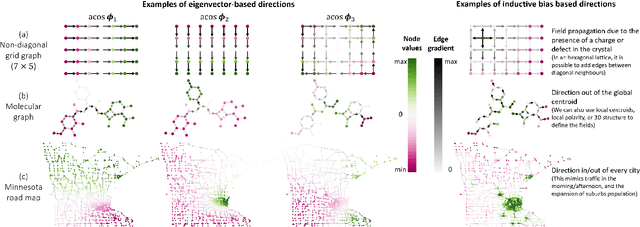
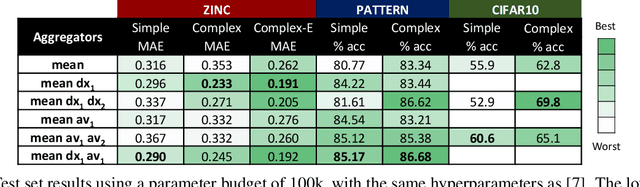
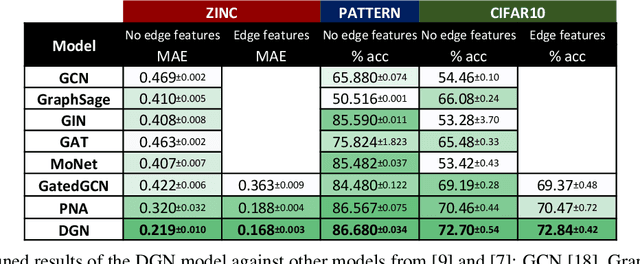
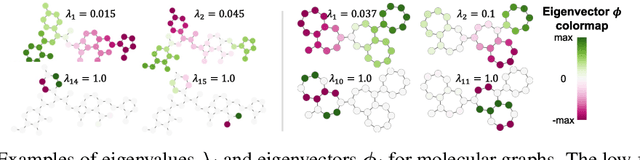
In order to overcome the expressive limitations of graph neural networks (GNNs), we propose the first method that exploits vector flows over graphs to develop globally consistent directional and asymmetric aggregation functions. We show that our directional graph networks (DGNs) generalize convolutional neural networks (CNNs) when applied on a grid. Whereas recent theoretical works focus on understanding local neighbourhoods, local structures and local isomorphism with no global information flow, our novel theoretical framework allows directional convolutional kernels in any graph. First, by defining a vector field in the graph, we develop a method of applying directional derivatives and smoothing by projecting node-specific messages into the field. Then we propose the use of the Laplacian eigenvectors as such vector field, and we show that the method generalizes CNNs on an n-dimensional grid. Finally, we bring the power of CNN data augmentation to graphs by providing a means of doing reflection, rotation and distortion on the underlying directional field. We evaluate our method on different standard benchmarks and see a relative error reduction of 8% on the CIFAR10 graph dataset and 11% to 32% on the molecular ZINC dataset. An important outcome of this work is that it enables to translate any physical or biological problems with intrinsic directional axes into a graph network formalism with an embedded directional field.

Principal Neighbourhood Aggregation for Graph Nets

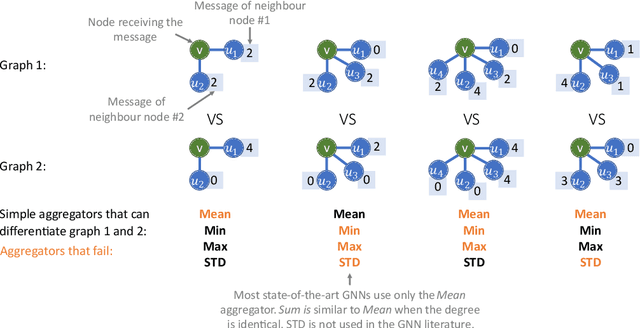
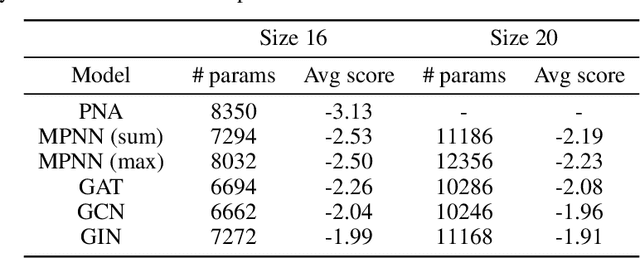
Graph Neural Networks (GNNs) have been shown to be effective models for different predictive tasks on graph-structured data. Recent work on their expressive power has focused on isomorphism tasks and countable feature spaces. We extend this theoretical framework to include continuous features - which occur regularly in real-world input domains and within the hidden layers of GNNs - and we demonstrate the requirement for multiple aggregation functions in this setting. Accordingly, we propose Principal Neighbourhood Aggregation (PNA), a novel architecture combining multiple aggregators with degree-scalers (which generalize the sum aggregator). Finally, we compare the capacity of different models to capture and exploit the graph structure via a benchmark containing multiple tasks taken from classical graph theory, which demonstrates the capacity of our model.

Improving Convolutional Neural Networks Via Conservative Field Regularisation and Integration

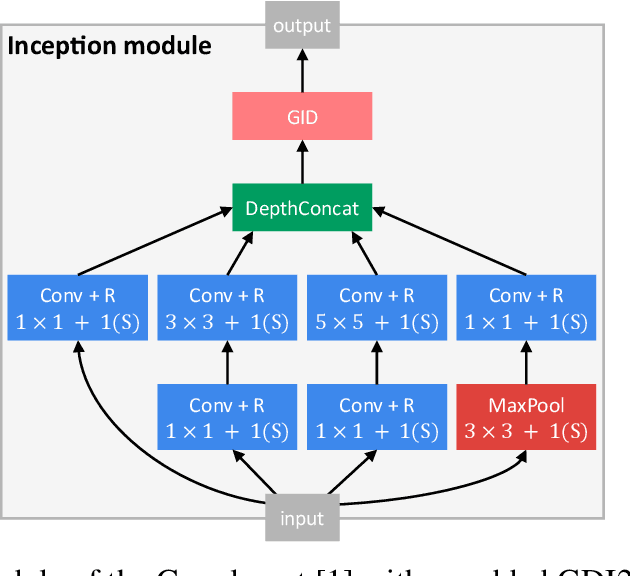
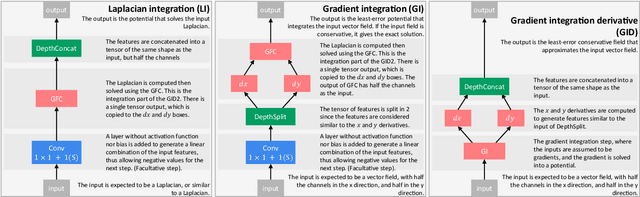
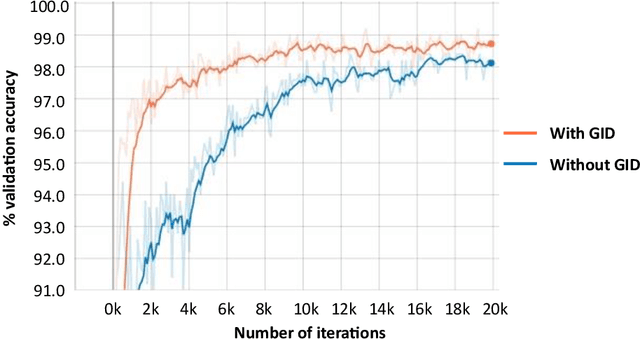
Current research in convolutional neural networks (CNN) focuses mainly on changing the architecture of the networks, optimizing the hyper-parameters and improving the gradient descent. However, most work use only 3 standard families of operations inside the CNN, the convolution, the activation function, and the pooling. In this work, we propose a new family of operations based on the Green's function of the Laplacian, which allows the network to solve the Laplacian, to integrate any vector field and to regularize the field by forcing it to be conservative. Hence, the Green's function (GF) is the first operation that regularizes the 2D or 3D feature space by forcing it to be conservative and physically interpretable, instead of regularizing the norm of the weights. Our results show that such regularization allows the network to learn faster, to have smoother training curves and to better generalize, without any additional parameter. The current manuscript presents early results, more work is required to benchmark the proposed method.

Saliency Enhancement using Gradient Domain Edges Merging

In recent years, there has been a rapid progress in solving the binary problems in computer vision, such as edge detection which finds the boundaries of an image and salient object detection which finds the important object in an image. This progress happened thanks to the rise of deep-learning and convolutional neural networks (CNN) which allow to extract complex and abstract features. However, edge detection and saliency are still two different fields and do not interact together, although it is intuitive for a human to detect salient objects based on its boundaries. Those features are not well merged in a CNN because edges and surfaces do not intersect since one feature represents a region while the other represents boundaries between different regions. In the current work, the main objective is to develop a method to merge the edges with the saliency maps to improve the performance of the saliency. Hence, we developed the gradient-domain merging (GDM) which can be used to quickly combine the image-domain information of salient object detection with the gradient-domain information of the edge detection. This leads to our proposed saliency enhancement using edges (SEE) with an average improvement of the F-measure of at least 3.4 times higher on the DUT-OMRON dataset and 6.6 times higher on the ECSSD dataset, when compared to competing algorithm such as denseCRF and BGOF. The SEE algorithm is split into 2 parts, SEE-Pre for preprocessing and SEE-Post pour postprocessing.

Deep Green Function Convolution for Improving Saliency in Convolutional Neural Networks

Current saliency methods require to learn large scale regional features using small convolutional kernels, which is not possible with a simple feed-forward network. Some methods solve this problem by using segmentation into superpixels while others downscale the image through the network and rescale it back to its original size. The objective of this paper is to show that saliency convolutional neural networks (CNN) can be improved by using a Green's function convolution (GFC) to extrapolate edges features into salient regions. The GFC acts as a gradient integrator, allowing to produce saliency features from thin edge-like features directly inside the CNN. Hence, we propose the gradient integration and sum (GIS) layer that combines the edges features with the saliency features. Using the HED and DSS architecture, we demonstrated that adding a GIS layer near the network's output allows to reduce the sensitivity to the parameter initialization and overfitting, thus improving the repeatability of the training. By adding a GIS layer to the state-of-the-art DSS model, there is an increase of 1.6% for the F-measure on the DUT-OMRON dataset, with only 10ms of additional computation time. The GIS layer further allows the network to perform significantly better in the case of highly noisy images or low-brightness images. In fact, we observed an F-measure improvement of 5.2% on noisy images and 2.8% on low-light images. Since the GIS layer is model agnostic, it can be implemented inside different fully convolutional networks, and it outperforms the denseCRF post-processing method and is 40 times faster. A major contribution of the current work is the first implementation of Green's function convolution inside a neural network, which allows the network, via very minor architectural changes and no additional parameters, to operate in the feature domain and in the gradient domain at the same time.