On computable learning of continuous features

We introduce definitions of computable PAC learning for binary classification over computable metric spaces. We provide sufficient conditions for learners that are empirical risk minimizers (ERM) to be computable, and bound the strong Weihrauch degree of an ERM learner under more general conditions. We also give a presentation of a hypothesis class that does not admit any proper computable PAC learner with computable sample function, despite the underlying class being PAC learnable.

Deep Involutive Generative Models for Neural MCMC

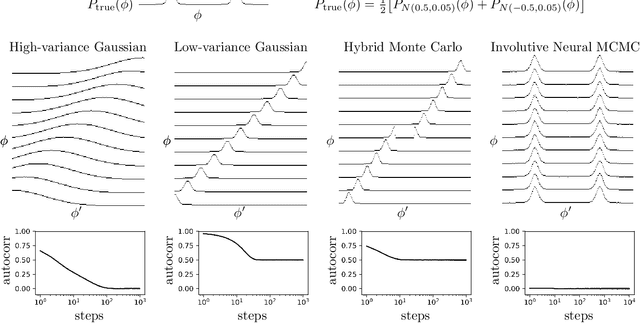
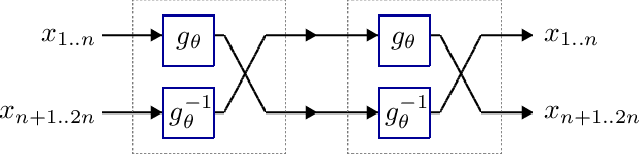
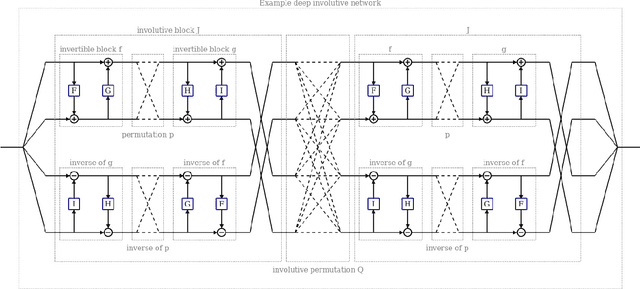
We introduce deep involutive generative models, a new architecture for deep generative modeling, and use them to define Involutive Neural MCMC, a new approach to fast neural MCMC. An involutive generative model represents a probability kernel $G(\phi \mapsto \phi')$ as an involutive (i.e., self-inverting) deterministic function $f(\phi, \pi)$ on an enlarged state space containing auxiliary variables $\pi$. We show how to make these models volume preserving, and how to use deep volume-preserving involutive generative models to make valid Metropolis-Hastings updates based on an auxiliary variable scheme with an easy-to-calculate acceptance ratio. We prove that deep involutive generative models and their volume-preserving special case are universal approximators for probability kernels. This result implies that with enough network capacity and training time, they can be used to learn arbitrarily complex MCMC updates. We define a loss function and optimization algorithm for training parameters given simulated data. We also provide initial experiments showing that Involutive Neural MCMC can efficiently explore multi-modal distributions that are intractable for Hybrid Monte Carlo, and can converge faster than A-NICE-MC, a recently introduced neural MCMC technique.

Priors on exchangeable directed graphs

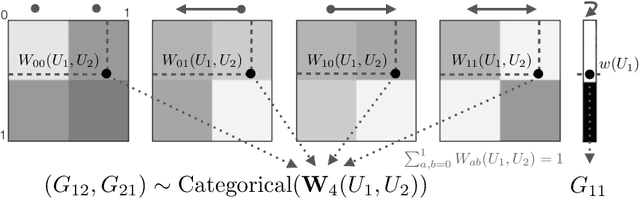
Directed graphs occur throughout statistical modeling of networks, and exchangeability is a natural assumption when the ordering of vertices does not matter. There is a deep structural theory for exchangeable undirected graphs, which extends to the directed case via measurable objects known as digraphons. Using digraphons, we first show how to construct models for exchangeable directed graphs, including special cases such as tournaments, linear orderings, directed acyclic graphs, and partial orderings. We then show how to construct priors on digraphons via the infinite relational digraphon model (di-IRM), a new Bayesian nonparametric block model for exchangeable directed graphs, and demonstrate inference on synthetic data.

An iterative step-function estimator for graphons

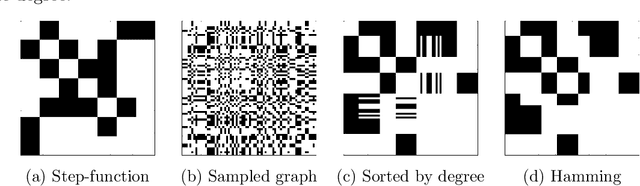
Exchangeable graphs arise via a sampling procedure from measurable functions known as graphons. A natural estimation problem is how well we can recover a graphon given a single graph sampled from it. One general framework for estimating a graphon uses step-functions obtained by partitioning the nodes of the graph according to some clustering algorithm. We propose an iterative step-function estimator (ISFE) that, given an initial partition, iteratively clusters nodes based on their edge densities with respect to the previous iteration's partition. We analyze ISFE and demonstrate its performance in comparison with other graphon estimation techniques.