Deep Ray
An optimal Petrov-Galerkin framework for operator networks
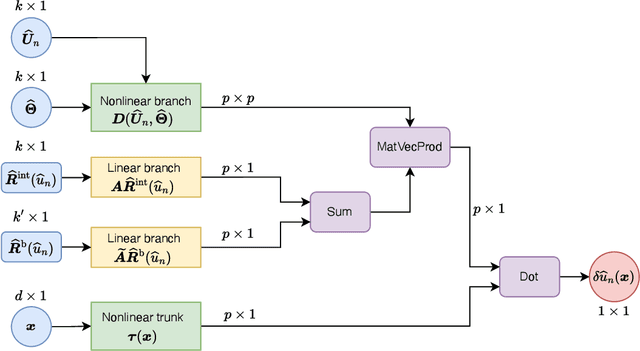
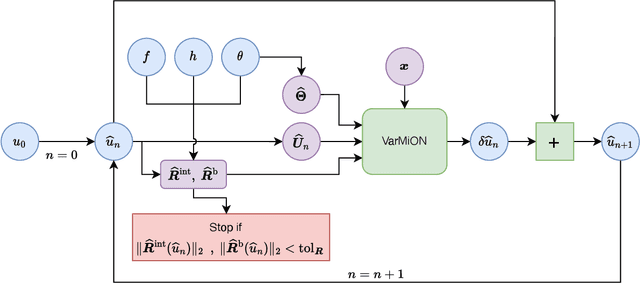
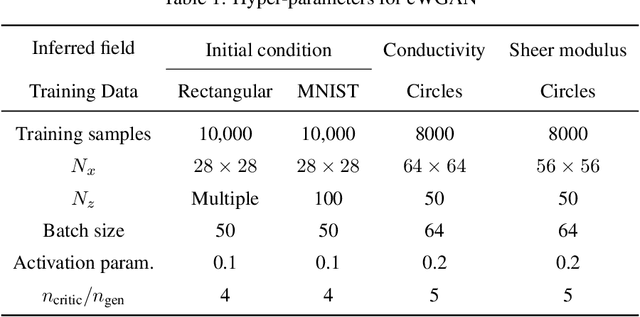
Mar 06, 2025Abstract:The optimal Petrov-Galerkin formulation to solve partial differential equations (PDEs) recovers the best approximation in a specified finite-dimensional (trial) space with respect to a suitable norm. However, the recovery of this optimal solution is contingent on being able to construct the optimal weighting functions associated with the trial basis. While explicit constructions are available for simple one- and two-dimensional problems, such constructions for a general multidimensional problem remain elusive. In the present work, we revisit the optimal Petrov-Galerkin formulation through the lens of deep learning. We propose an operator network framework called Petrov-Galerkin Variationally Mimetic Operator Network (PG-VarMiON), which emulates the optimal Petrov-Galerkin weak form of the underlying PDE. The PG-VarMiON is trained in a supervised manner using a labeled dataset comprising the PDE data and the corresponding PDE solution, with the training loss depending on the choice of the optimal norm. The special architecture of the PG-VarMiON allows it to implicitly learn the optimal weighting functions, thus endowing the proposed operator network with the ability to generalize well beyond the training set. We derive approximation error estimates for PG-VarMiON, highlighting the contributions of various error sources, particularly the error in learning the true weighting functions. Several numerical results are presented for the advection-diffusion equation to demonstrate the efficacy of the proposed method. By embedding the Petrov-Galerkin structure into the network architecture, PG-VarMiON exhibits greater robustness and improved generalization compared to other popular deep operator frameworks, particularly when the training data is limited.
Learning WENO for entropy stable schemes to solve conservation laws
Mar 21, 2024Abstract:Entropy conditions play a crucial role in the extraction of a physically relevant solution for a system of conservation laws, thus motivating the construction of entropy stable schemes that satisfy a discrete analogue of such conditions. TeCNO schemes (Fjordholm et al. 2012) form a class of arbitrary high-order entropy stable finite difference solvers, which require specialized reconstruction algorithms satisfying the sign property at each cell interface. Recently, third-order WENO schemes called SP-WENO (Fjordholm and Ray, 2016) and SP-WENOc (Ray, 2018) have been designed to satisfy the sign property. However, these WENO algorithms can perform poorly near shocks, with the numerical solutions exhibiting large spurious oscillations. In the present work, we propose a variant of the SP-WENO, termed as Deep Sign-Preserving WENO (DSP-WENO), where a neural network is trained to learn the WENO weighting strategy. The sign property and third-order accuracy are strongly imposed in the algorithm, which constrains the WENO weight selection region to a convex polygon. Thereafter, a neural network is trained to select the WENO weights from this convex region with the goal of improving the shock-capturing capabilities without sacrificing the rate of convergence in smooth regions. The proposed synergistic approach retains the mathematical framework of the TeCNO scheme while integrating deep learning to remedy the computational issues of the WENO-based reconstruction. We present several numerical experiments to demonstrate the significant improvement with DSP-WENO over the existing variants of WENO satisfying the sign property.
Generative Algorithms for Fusion of Physics-Based Wildfire Spread Models with Satellite Data for Initializing Wildfire Forecasts
Sep 05, 2023Abstract:Increases in wildfire activity and the resulting impacts have prompted the development of high-resolution wildfire behavior models for forecasting fire spread. Recent progress in using satellites to detect fire locations further provides the opportunity to use measurements to improve fire spread forecasts from numerical models through data assimilation. This work develops a method for inferring the history of a wildfire from satellite measurements, providing the necessary information to initialize coupled atmosphere-wildfire models from a measured wildfire state in a physics-informed approach. The fire arrival time, which is the time the fire reaches a given spatial location, acts as a succinct representation of the history of a wildfire. In this work, a conditional Wasserstein Generative Adversarial Network (cWGAN), trained with WRF-SFIRE simulations, is used to infer the fire arrival time from satellite active fire data. The cWGAN is used to produce samples of likely fire arrival times from the conditional distribution of arrival times given satellite active fire detections. Samples produced by the cWGAN are further used to assess the uncertainty of predictions. The cWGAN is tested on four California wildfires occurring between 2020 and 2022, and predictions for fire extent are compared against high resolution airborne infrared measurements. Further, the predicted ignition times are compared with reported ignition times. An average Sorensen's coefficient of 0.81 for the fire perimeters and an average ignition time error of 32 minutes suggest that the method is highly accurate.
Learning end-to-end inversion of circular Radon transforms in the partial radial setup
Aug 27, 2023



Abstract:We present a deep learning-based computational algorithm for inversion of circular Radon transforms in the partial radial setup, arising in photoacoustic tomography. We first demonstrate that the truncated singular value decomposition-based method, which is the only traditional algorithm available to solve this problem, leads to severe artifacts which renders the reconstructed field as unusable. With the objective of overcoming this computational bottleneck, we train a ResBlock based U-Net to recover the inferred field that directly operates on the measured data. Numerical results with augmented Shepp-Logan phantoms, in the presence of noisy full and limited view data, demonstrate the superiority of the proposed algorithm.
Solution of physics-based inverse problems using conditional generative adversarial networks with full gradient penalty
Jun 08, 2023Abstract:The solution of probabilistic inverse problems for which the corresponding forward problem is constrained by physical principles is challenging. This is especially true if the dimension of the inferred vector is large and the prior information about it is in the form of a collection of samples. In this work, a novel deep learning based approach is developed and applied to solving these types of problems. The approach utilizes samples of the inferred vector drawn from the prior distribution and a physics-based forward model to generate training data for a conditional Wasserstein generative adversarial network (cWGAN). The cWGAN learns the probability distribution for the inferred vector conditioned on the measurement and produces samples from this distribution. The cWGAN developed in this work differs from earlier versions in that its critic is required to be 1-Lipschitz with respect to both the inferred and the measurement vectors and not just the former. This leads to a loss term with the full (and not partial) gradient penalty. It is shown that this rather simple change leads to a stronger notion of convergence for the conditional density learned by the cWGAN and a more robust and accurate sampling strategy. Through numerical examples it is shown that this change also translates to better accuracy when solving inverse problems. The numerical examples considered include illustrative problems where the true distribution and/or statistics are known, and a more complex inverse problem motivated by applications in biomechanics.
Deep Learning and Computational Physics (Lecture Notes)
Jan 03, 2023



Abstract:These notes were compiled as lecture notes for a course developed and taught at the University of the Southern California. They should be accessible to a typical engineering graduate student with a strong background in Applied Mathematics. The main objective of these notes is to introduce a student who is familiar with concepts in linear algebra and partial differential equations to select topics in deep learning. These lecture notes exploit the strong connections between deep learning algorithms and the more conventional techniques of computational physics to achieve two goals. First, they use concepts from computational physics to develop an understanding of deep learning algorithms. Not surprisingly, many concepts in deep learning can be connected to similar concepts in computational physics, and one can utilize this connection to better understand these algorithms. Second, several novel deep learning algorithms can be used to solve challenging problems in computational physics. Thus, they offer someone who is interested in modeling a physical phenomena with a complementary set of tools.
Variationally Mimetic Operator Networks
Sep 26, 2022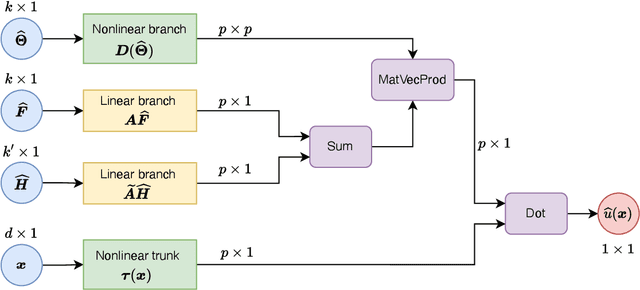

Abstract:Operator networks have emerged as promising deep learning tools for approximating the solution to partial differential equations (PDEs). These networks map input functions that describe material properties, forcing functions and boundary data to the solution of a PDE. This work describes a new architecture for operator networks that mimics the form of the numerical solution obtained from an approximation of the variational or weak formulation of the problem. The application of these ideas to a generic elliptic PDE leads to a variationally mimetic operator network (VarMiON). Like the conventional Deep Operator Network (DeepONet) the VarMiON is also composed of a sub-network that constructs the basis functions for the output and another that constructs the coefficients for these basis functions. However, in contrast to the DeepONet, in the VarMiON the architecture of these networks is precisely determined. An analysis of the error in the VarMiON solution reveals that it contains contributions from the error in the training data, the training error, quadrature error in sampling input and output functions, and a "covering error" that measures the distance between the test input functions and the nearest functions in the training dataset. It also depends on the stability constants for the exact network and its VarMiON approximation. The application of the VarMiON to a canonical elliptic PDE reveals that for approximately the same number of network parameters, on average the VarMiON incurs smaller errors than a standard DeepONet. Further, its performance is more robust to variations in input functions, the techniques used to sample the input and output functions, the techniques used to construct the basis functions, and the number of input functions.
The efficacy and generalizability of conditional GANs for posterior inference in physics-based inverse problems
Feb 15, 2022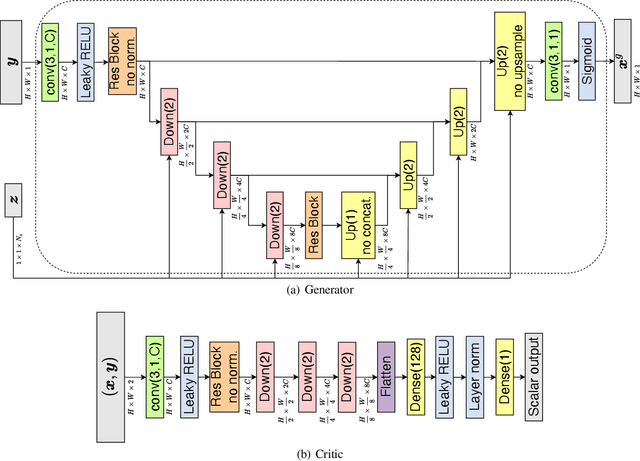
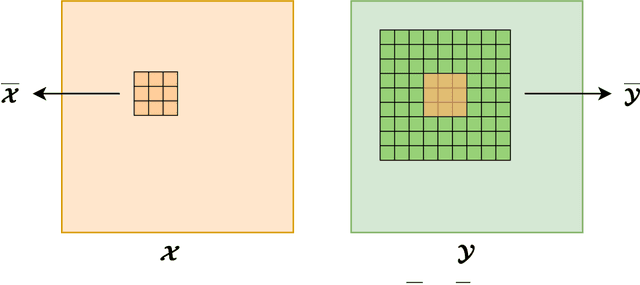
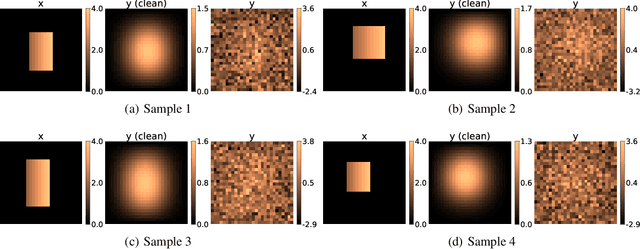
Abstract:In this work, we train conditional Wasserstein generative adversarial networks to effectively sample from the posterior of physics-based Bayesian inference problems. The generator is constructed using a U-Net architecture, with the latent information injected using conditional instance normalization. The former facilitates a multiscale inverse map, while the latter enables the decoupling of the latent space dimension from the dimension of the measurement, and introduces stochasticity at all scales of the U-Net. We solve PDE-based inverse problems to demonstrate the performance of our approach in quantifying the uncertainty in the inferred field. Further, we show the generator can learn inverse maps which are local in nature, which in turn promotes generalizability when testing with out-of-distribution samples.
Solution of Physics-based Bayesian Inverse Problems with Deep Generative Priors
Jul 06, 2021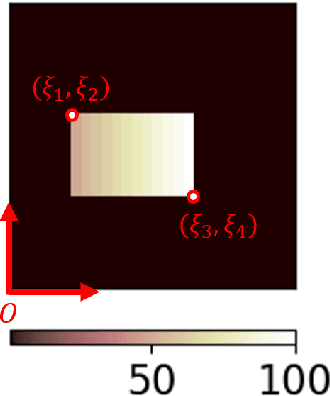
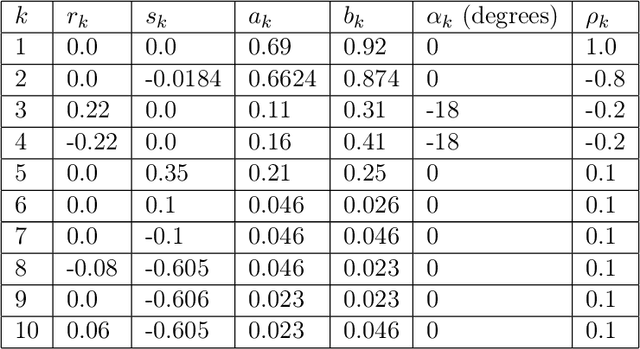
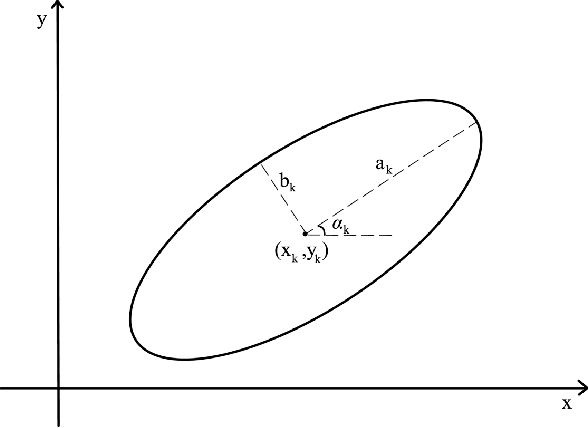
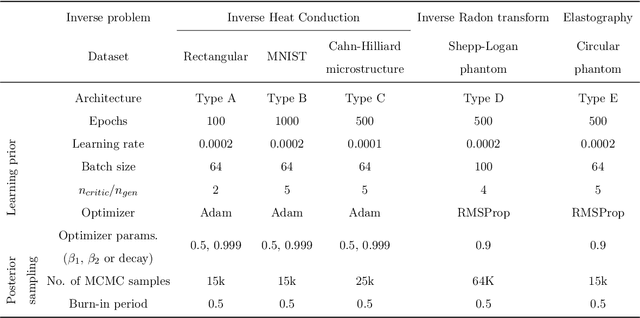
Abstract:Inverse problems are notoriously difficult to solve because they can have no solutions, multiple solutions, or have solutions that vary significantly in response to small perturbations in measurements. Bayesian inference, which poses an inverse problem as a stochastic inference problem, addresses these difficulties and provides quantitative estimates of the inferred field and the associated uncertainty. However, it is difficult to employ when inferring vectors of large dimensions, and/or when prior information is available through previously acquired samples. In this paper, we describe how deep generative adversarial networks can be used to represent the prior distribution in Bayesian inference and overcome these challenges. We apply these ideas to inverse problems that are diverse in terms of the governing physical principles, sources of prior knowledge, type of measurement, and the extent of available information about measurement noise. In each case we apply the proposed approach to infer the most likely solution and quantitative estimates of uncertainty.
Iterative Surrogate Model Optimization (ISMO): An active learning algorithm for PDE constrained optimization with deep neural networks
Aug 13, 2020


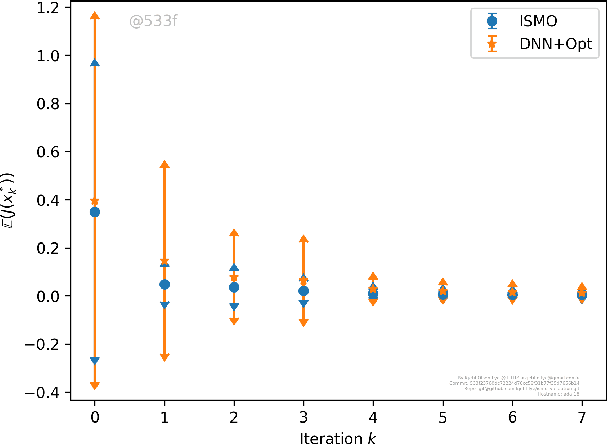
Abstract:We present a novel active learning algorithm, termed as iterative surrogate model optimization (ISMO), for robust and efficient numerical approximation of PDE constrained optimization problems. This algorithm is based on deep neural networks and its key feature is the iterative selection of training data through a feedback loop between deep neural networks and any underlying standard optimization algorithm. Under suitable hypotheses, we show that the resulting optimizers converge exponentially fast (and with exponentially decaying variance), with respect to increasing number of training samples. Numerical examples for optimal control, parameter identification and shape optimization problems for PDEs are provided to validate the proposed theory and to illustrate that ISMO significantly outperforms a standard deep neural network based surrogate optimization algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge