Iterative Surrogate Model Optimization (ISMO): An active learning algorithm for PDE constrained optimization with deep neural networks

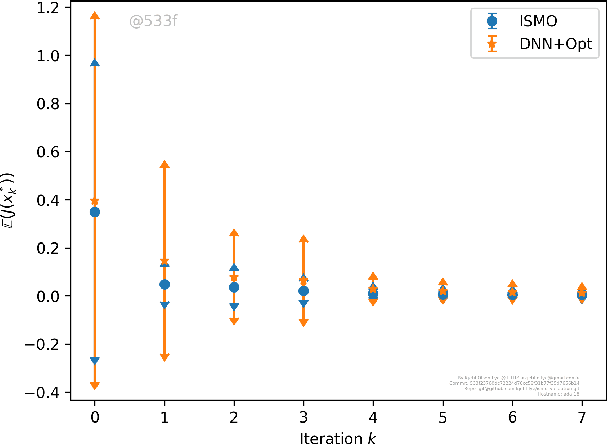
We present a novel active learning algorithm, termed as iterative surrogate model optimization (ISMO), for robust and efficient numerical approximation of PDE constrained optimization problems. This algorithm is based on deep neural networks and its key feature is the iterative selection of training data through a feedback loop between deep neural networks and any underlying standard optimization algorithm. Under suitable hypotheses, we show that the resulting optimizers converge exponentially fast (and with exponentially decaying variance), with respect to increasing number of training samples. Numerical examples for optimal control, parameter identification and shape optimization problems for PDEs are provided to validate the proposed theory and to illustrate that ISMO significantly outperforms a standard deep neural network based surrogate optimization algorithm.

A Multi-level procedure for enhancing accuracy of machine learning algorithms

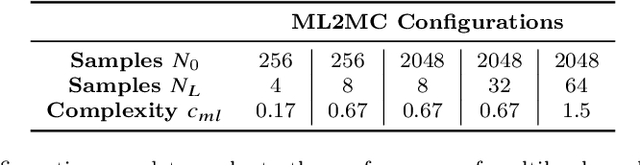
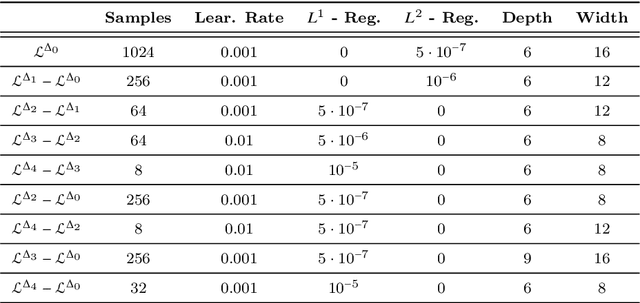
We propose a multi-level method to increase the accuracy of machine learning algorithms for approximating observables in scientific computing, particularly those that arise in systems modeled by differential equations. The algorithm relies on judiciously combining a large number of computationally cheap training data on coarse resolutions with a few expensive training samples on fine grid resolutions. Theoretical arguments for lowering the generalization error, based on reducing the variance of the underlying maps, are provided and numerical evidence, indicating significant gains over underlying single-level machine learning algorithms, are presented. Moreover, we also apply the multi-level algorithm in the context of forward uncertainty quantification and observe a considerable speed-up over competing algorithms.

Deep learning observables in computational fluid dynamics

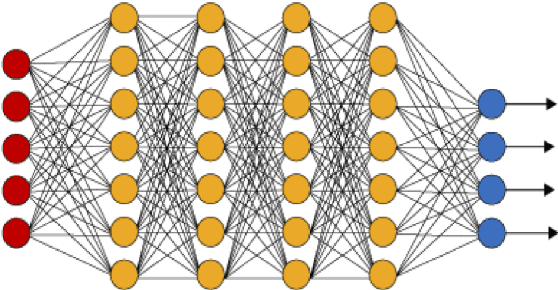
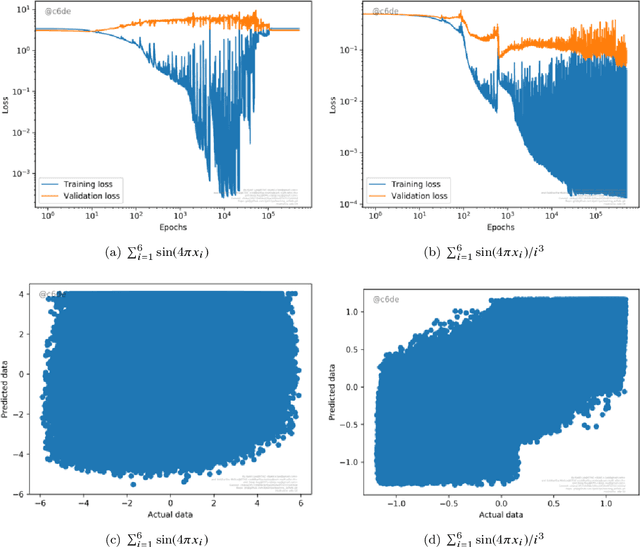
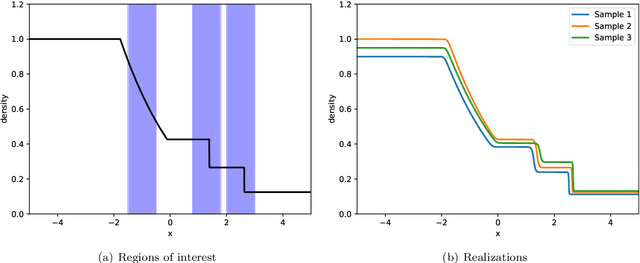
Many large scale problems in computational fluid dynamics such as uncertainty quantification, Bayesian inversion, data assimilation and PDE constrained optimization are considered very challenging computationally as they require a large number of expensive (forward) numerical solutions of the corresponding PDEs. We propose a machine learning algorithm, based on deep artificial neural networks, that learns the underlying input parameters to observable map from a few training samples (computed realizations of this map). By a judicious combination of theoretical arguments and empirical observations, we find suitable network architectures and training hyperparameters that result in robust and efficient neural network approximations of the parameters to observable map. Numerical experiments for realistic high dimensional test problems, demonstrate that even with approximately 100 training samples, the resulting neural networks have a prediction error of less than one to two percent, at a computational cost which is several orders of magnitude lower than the cost of the underlying PDE solver. Moreover, we combine the proposed deep learning algorithm with Monte Carlo (MC) and Quasi-Monte Carlo (QMC) methods to efficiently compute uncertainty propagation for nonlinear PDEs. Under the assumption that the underlying neural networks generalize well, we prove that the deep learning MC and QMC algorithms are guaranteed to be faster than the baseline (quasi-) Monte Carlo methods. Numerical experiments demonstrating one to two orders of magnitude speed up over baseline QMC and MC algorithms, for the intricate problem of computing probability distributions of the observable, are also presented.