Time-dependent density estimation using binary classifiers

We propose a data-driven method to learn the time-dependent probability density of a multivariate stochastic process from sample paths, assuming that the initial probability density is known and can be evaluated. Our method uses a novel time-dependent binary classifier trained using a contrastive estimation-based objective that trains the classifier to discriminate between realizations of the stochastic process at two nearby time instants. Significantly, the proposed method explicitly models the time-dependent probability distribution, which means that it is possible to obtain the value of the probability density within the time horizon of interest. Additionally, the input before the final activation in the time-dependent classifier is a second-order approximation to the partial derivative, with respect to time, of the logarithm of the density. We apply the proposed approach to approximate the time-dependent probability density functions for systems driven by stochastic excitations. We also use the proposed approach to synthesize new samples of a random vector from a given set of its realizations. In such applications, we generate sample paths necessary for training using stochastic interpolants. Subsequently, new samples are generated using gradient-based Markov chain Monte Carlo methods because automatic differentiation can efficiently provide the necessary gradient. Further, we demonstrate the utility of an explicit approximation to the time-dependent probability density function through applications in unsupervised outlier detection. Through several numerical experiments, we show that the proposed method accurately reconstructs complex time-dependent, multi-modal, and near-degenerate densities, scales effectively to moderately high-dimensional problems, and reliably detects rare events among real-world data.

Generative Algorithms for Wildfire Progression Reconstruction from Multi-Modal Satellite Active Fire Measurements and Terrain Height

Increasing wildfire occurrence has spurred growing interest in wildfire spread prediction. However, even the most complex wildfire models diverge from observed progression during multi-day simulations, motivating need for data assimilation. A useful approach to assimilating measurement data into complex coupled atmosphere-wildfire models is to estimate wildfire progression from measurements and use this progression to develop a matching atmospheric state. In this study, an approach is developed for estimating fire progression from VIIRS active fire measurements, GOES-derived ignition times, and terrain height data. A conditional Generative Adversarial Network is trained with simulations of historic wildfires from the atmosphere-wildfire model WRF-SFIRE, thus allowing incorporation of WRF-SFIRE physics into estimates. Fire progression is succinctly represented by fire arrival time, and measurements for training are obtained by applying an approximate observation operator to WRF-SFIRE solutions, eliminating need for satellite data during training. The model is trained on tuples of fire arrival times, measurements, and terrain, and once trained leverages measurements of real fires and corresponding terrain data to generate samples of fire arrival times. The approach is validated on five Pacific US wildfires, with results compared against high-resolution perimeters measured via aircraft, finding an average Sorensen-Dice coefficient of 0.81. The influence of terrain height on the arrival time inference is also evaluated and it is observed that terrain has minimal influence when the inference is conditioned on satellite measurements.

Unifying and extending Diffusion Models through PDEs for solving Inverse Problems

Diffusion models have emerged as powerful generative tools with applications in computer vision and scientific machine learning (SciML), where they have been used to solve large-scale probabilistic inverse problems. Traditionally, these models have been derived using principles of variational inference, denoising, statistical signal processing, and stochastic differential equations. In contrast to the conventional presentation, in this study we derive diffusion models using ideas from linear partial differential equations and demonstrate that this approach has several benefits that include a constructive derivation of the forward and reverse processes, a unified derivation of multiple formulations and sampling strategies, and the discovery of a new class of models. We also apply the conditional version of these models to solving canonical conditional density estimation problems and challenging inverse problems. These problems help establish benchmarks for systematically quantifying the performance of different formulations and sampling strategies in this study, and for future studies. Finally, we identify and implement a mechanism through which a single diffusion model can be applied to measurements obtained from multiple measurement operators. Taken together, the contents of this manuscript provide a new understanding and several new directions in the application of diffusion models to solving physics-based inverse problems.

Memorization and Regularization in Generative Diffusion Models

Diffusion models have emerged as a powerful framework for generative modeling. At the heart of the methodology is score matching: learning gradients of families of log-densities for noisy versions of the data distribution at different scales. When the loss function adopted in score matching is evaluated using empirical data, rather than the population loss, the minimizer corresponds to the score of a time-dependent Gaussian mixture. However, use of this analytically tractable minimizer leads to data memorization: in both unconditioned and conditioned settings, the generative model returns the training samples. This paper contains an analysis of the dynamical mechanism underlying memorization. The analysis highlights the need for regularization to avoid reproducing the analytically tractable minimizer; and, in so doing, lays the foundations for a principled understanding of how to regularize. Numerical experiments investigate the properties of: (i) Tikhonov regularization; (ii) regularization designed to promote asymptotic consistency; and (iii) regularizations induced by under-parameterization of a neural network or by early stopping when training a neural network. These experiments are evaluated in the context of memorization, and directions for future development of regularization are highlighted.

Diffusion Models for Generating Ballistic Spacecraft Trajectories

Generative modeling has drawn much attention in creative and scientific data generation tasks. Score-based Diffusion Models, a type of generative model that iteratively learns to denoise data, have shown state-of-the-art results on tasks such as image generation, multivariate time series forecasting, and robotic trajectory planning. Using score-based diffusion models, this work implements a novel generative framework to generate ballistic transfers from Earth to Mars. We further analyze the model's ability to learn the characteristics of the original dataset and its ability to produce transfers that follow the underlying dynamics. Ablation studies were conducted to determine how model performance varies with model size and trajectory temporal resolution. In addition, a performance benchmark is designed to assess the generative model's usefulness for trajectory design, conduct model performance comparisons, and lay the groundwork for evaluating different generative models for trajectory design beyond diffusion. The results of this analysis showcase several useful properties of diffusion models that, when taken together, can enable a future system for generative trajectory design powered by diffusion models.

Solution of physics-based inverse problems using conditional generative adversarial networks with full gradient penalty

The solution of probabilistic inverse problems for which the corresponding forward problem is constrained by physical principles is challenging. This is especially true if the dimension of the inferred vector is large and the prior information about it is in the form of a collection of samples. In this work, a novel deep learning based approach is developed and applied to solving these types of problems. The approach utilizes samples of the inferred vector drawn from the prior distribution and a physics-based forward model to generate training data for a conditional Wasserstein generative adversarial network (cWGAN). The cWGAN learns the probability distribution for the inferred vector conditioned on the measurement and produces samples from this distribution. The cWGAN developed in this work differs from earlier versions in that its critic is required to be 1-Lipschitz with respect to both the inferred and the measurement vectors and not just the former. This leads to a loss term with the full (and not partial) gradient penalty. It is shown that this rather simple change leads to a stronger notion of convergence for the conditional density learned by the cWGAN and a more robust and accurate sampling strategy. Through numerical examples it is shown that this change also translates to better accuracy when solving inverse problems. The numerical examples considered include illustrative problems where the true distribution and/or statistics are known, and a more complex inverse problem motivated by applications in biomechanics.

Uncertainty quantification for ptychography using normalizing flows

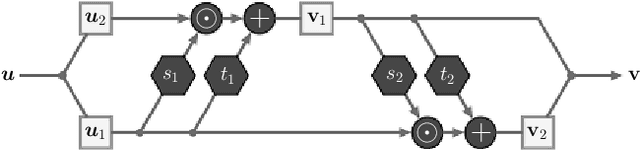
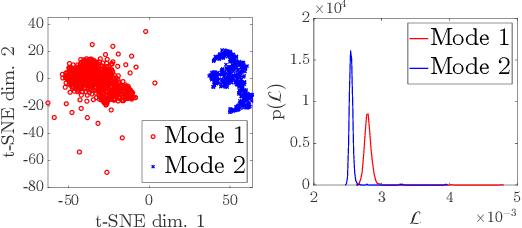
Ptychography, as an essential tool for high-resolution and nondestructive material characterization, presents a challenging large-scale nonlinear and non-convex inverse problem; however, its intrinsic photon statistics create clear opportunities for statistical-based deep learning approaches to tackle these challenges, which has been underexplored. In this work, we explore normalizing flows to obtain a surrogate for the high-dimensional posterior, which also enables the characterization of the uncertainty associated with the reconstruction: an extremely desirable capability when judging the reconstruction quality in the absence of ground truth, spotting spurious artifacts and guiding future experiments using the returned uncertainty patterns. We demonstrate the performance of the proposed method on a synthetic sample with added noise and in various physical experimental settings.

Gaussian Process for Tomography

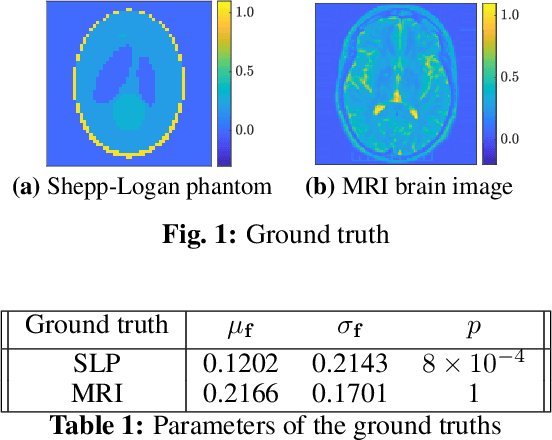
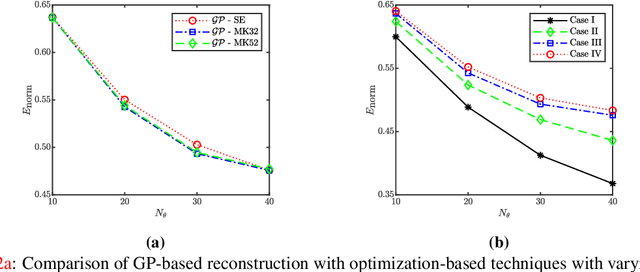
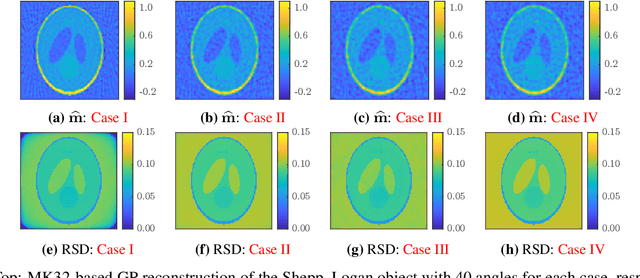
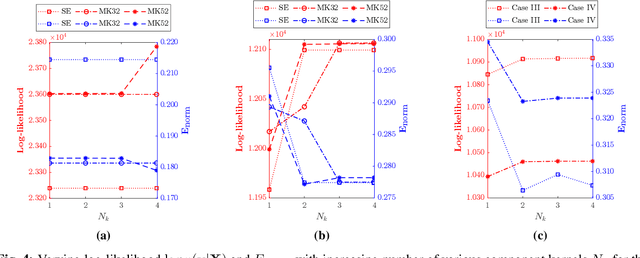
Tomographic reconstruction, despite its revolutionary impact on a wide range of applications, suffers from its ill-posed nature in that there is no unique solution because of limited and noisy measurements. Traditional optimization-based reconstruction relies on regularization to address this issue; however, it faces its own challenge because the type of regularizer and choice of regularization parameter are a critical but difficult decision. Moreover, traditional reconstruction yields point estimates for the reconstruction with no further indication of the quality of the solution. In this work we address these challenges by exploring Gaussian processes (GPs). Our proposed GP approach yields not only the reconstructed object through the posterior mean but also a quantification of the solution uncertainties through the posterior covariance. Furthermore, we explore the flexibility of the GP framework to provide a robust model of the information across various length scales in the object, as well as the complex noise in the measurements. We illustrate the proposed approach on both synthetic and real tomography images and show its unique capability of uncertainty quantification in the presence of various types of noise, as well as reconstruction comparison with existing methods.