Bounding Causal Effects with Leaky Instruments

Instrumental variables (IVs) are a popular and powerful tool for estimating causal effects in the presence of unobserved confounding. However, classical approaches rely on strong assumptions such as the $\textit{exclusion criterion}$, which states that instrumental effects must be entirely mediated by treatments. This assumption often fails in practice. When IV methods are improperly applied to data that do not meet the exclusion criterion, estimated causal effects may be badly biased. In this work, we propose a novel solution that provides $\textit{partial}$ identification in linear models given a set of $\textit{leaky instruments}$, which are allowed to violate the exclusion criterion to some limited degree. We derive a convex optimization objective that provides provably sharp bounds on the average treatment effect under some common forms of information leakage, and implement inference procedures to quantify the uncertainty of resulting estimates. We demonstrate our method in a set of experiments with simulated data, where it performs favorably against the state of the art.

Explaining Predictive Uncertainty with Information Theoretic Shapley Values

Researchers in explainable artificial intelligence have developed numerous methods for helping users understand the predictions of complex supervised learning models. By contrast, explaining the $\textit{uncertainty}$ of model outputs has received relatively little attention. We adapt the popular Shapley value framework to explain various types of predictive uncertainty, quantifying each feature's contribution to the conditional entropy of individual model outputs. We consider games with modified characteristic functions and find deep connections between the resulting Shapley values and fundamental quantities from information theory and conditional independence testing. We outline inference procedures for finite sample error rate control with provable guarantees, and implement an efficient algorithm that performs well in a range of experiments on real and simulated data. Our method has applications to covariate shift detection, active learning, feature selection, and active feature-value acquisition.

Intervention Generalization: A View from Factor Graph Models

One of the goals of causal inference is to generalize from past experiments and observational data to novel conditions. While it is in principle possible to eventually learn a mapping from a novel experimental condition to an outcome of interest, provided a sufficient variety of experiments is available in the training data, coping with a large combinatorial space of possible interventions is hard. Under a typical sparse experimental design, this mapping is ill-posed without relying on heavy regularization or prior distributions. Such assumptions may or may not be reliable, and can be hard to defend or test. In this paper, we take a close look at how to warrant a leap from past experiments to novel conditions based on minimal assumptions about the factorization of the distribution of the manipulated system, communicated in the well-understood language of factor graph models. A postulated $\textit{interventional factor model}$ (IFM) may not always be informative, but it conveniently abstracts away a need for explicit unmeasured confounding and feedback mechanisms, leading to directly testable claims. We derive necessary and sufficient conditions for causal effect identifiability with IFMs using data from a collection of experimental settings, and implement practical algorithms for generalizing expected outcomes to novel conditions never observed in the data.

Conditional Feature Importance for Mixed Data

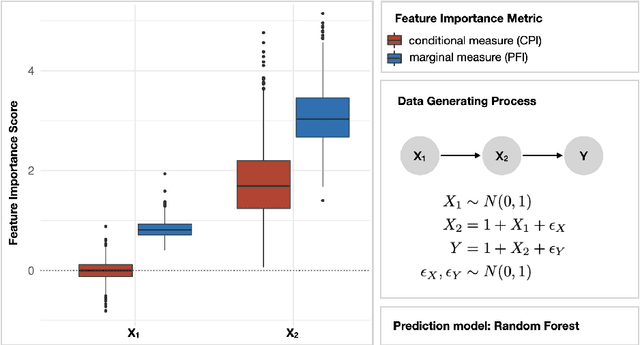
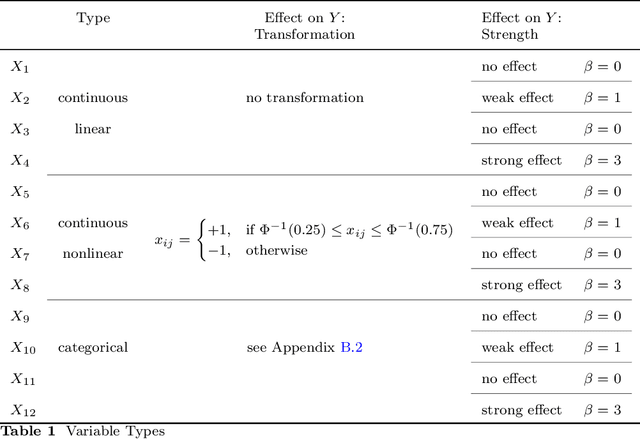
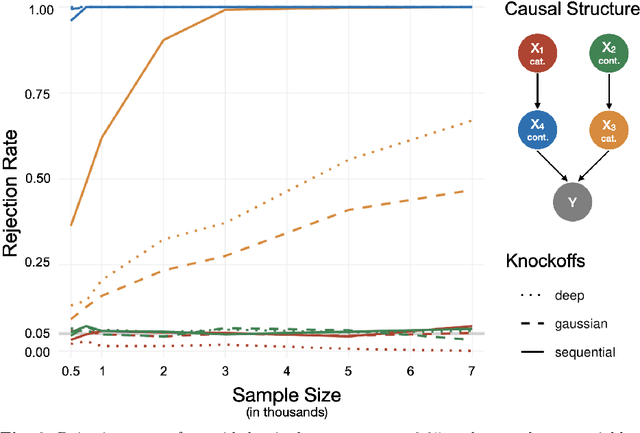
Despite the popularity of feature importance measures in interpretable machine learning, the statistical adequacy of these methods is rarely discussed. From a statistical perspective, a major distinction is between analyzing a variable's importance before and after adjusting for covariates - i.e., between marginal and conditional measures. Our work draws attention to this rarely acknowledged, yet crucial distinction and showcases its implications. Further, we reveal that for testing conditional feature importance (CFI), only few methods are available and practitioners have hitherto been severely restricted in method application due to mismatching data requirements. Most real-world data exhibits complex feature dependencies and incorporates both continuous and categorical data (mixed data). Both properties are oftentimes neglected by CFI measures. To fill this gap, we propose to combine the conditional predictive impact (CPI) framework (arXiv:1901.09917) with sequential knockoff sampling (arXiv:2010.14026). The CPI enables CFI measurement that controls for any feature dependencies by sampling valid knockoffs - hence, generating synthetic data with similar statistical properties - for the data to be analyzed. Sequential knockoffs were deliberately designed to handle mixed data and thus allow us to extend the CPI approach to such datasets. We demonstrate through numerous simulations and a real-world example that our proposed workflow controls type I error, achieves high power and is in line with results given by other CFI measures, whereas marginal feature importance metrics result in misleading interpretations. Our findings highlight the necessity of developing statistically adequate, specialized methods for mixed data.

Smooth densities and generative modeling with unsupervised random forests

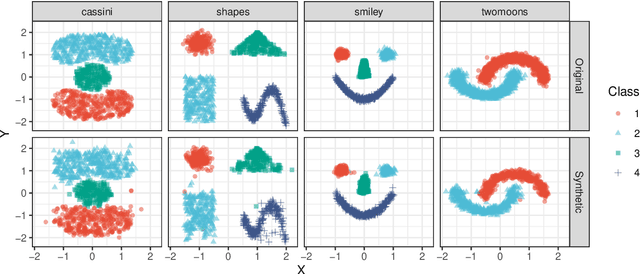
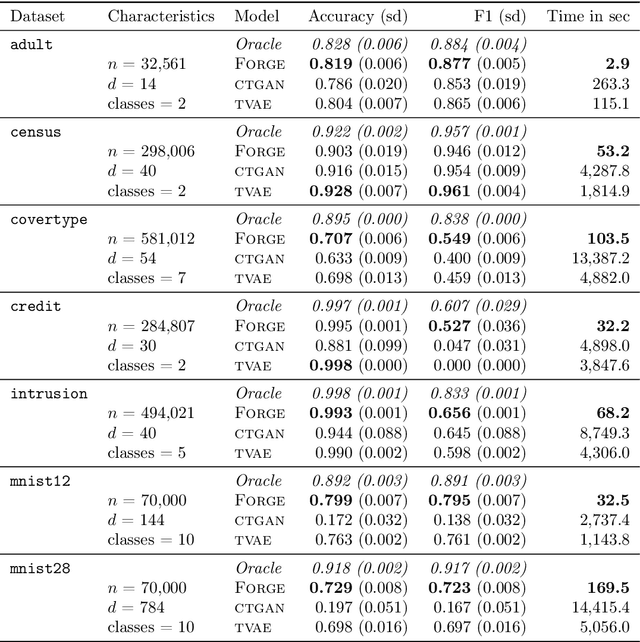
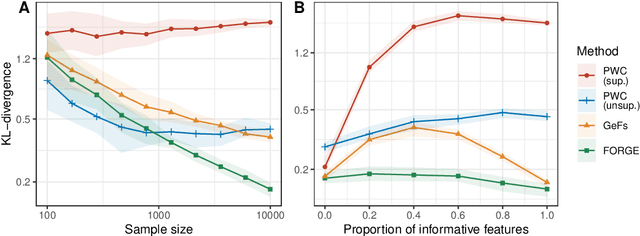
Density estimation is a fundamental problem in statistics, and any attempt to do so in high dimensions typically requires strong assumptions or complex deep learning architectures. An important application for density estimators is synthetic data generation, an area currently dominated by neural networks that often demand enormous training datasets and extensive tuning. We propose a new method based on unsupervised random forests for estimating smooth densities in arbitrary dimensions without parametric constraints, as well as generating realistic synthetic data. We prove the consistency of our approach and demonstrate its advantages over existing tree-based density estimators, which generally rely on ill-chosen split criteria and do not scale well with data dimensionality. Experiments illustrate that our algorithm compares favorably to state-of-the-art deep learning generative models, achieving superior performance in a range of benchmark trials while executing about two orders of magnitude faster on average. Our method is implemented in easy-to-use $\texttt{R}$ and Python packages.

Rational Shapley Values

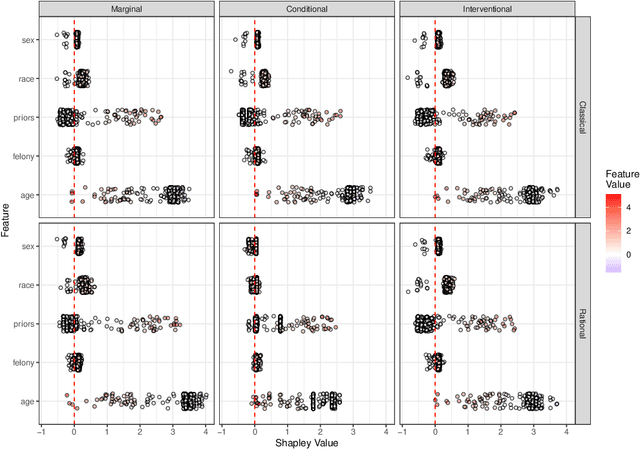
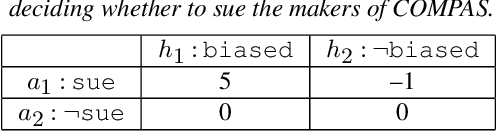
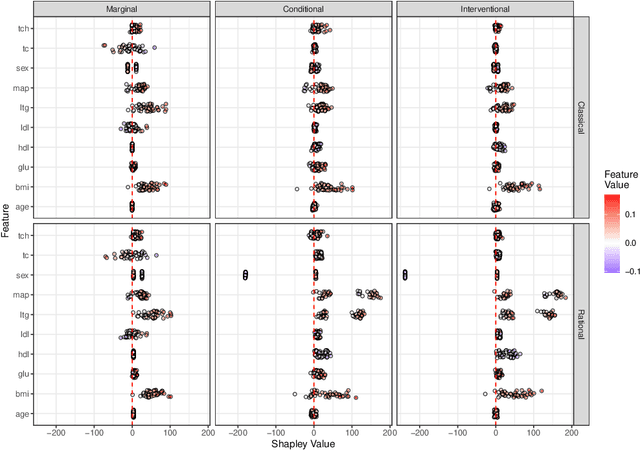
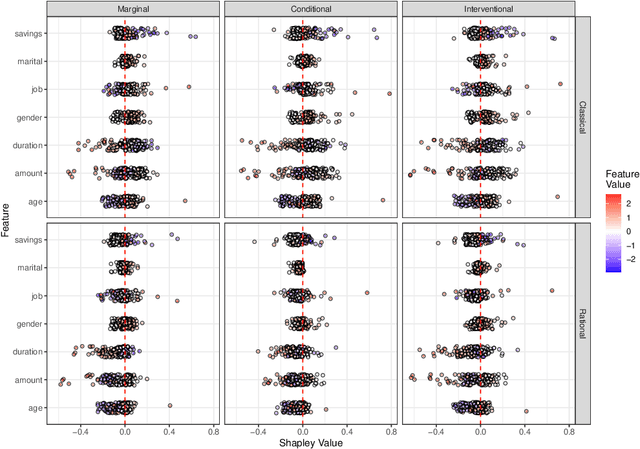
Explaining the predictions of opaque machine learning algorithms is an important and challenging task, especially as complex models are increasingly used to assist in high-stakes decisions such as those arising in healthcare and finance. Most popular tools for post-hoc explainable artificial intelligence (XAI) are either insensitive to context (e.g., feature attributions) or difficult to summarize (e.g., counterfactuals). In this paper, I introduce \emph{rational Shapley values}, a novel XAI method that synthesizes and extends these seemingly incompatible approaches in a rigorous, flexible manner. I leverage tools from decision theory and causal modeling to formalize and implement a pragmatic approach that resolves a number of known challenges in XAI. By pairing the distribution of random variables with the appropriate reference class for a given explanation task, I illustrate through theory and experiments how user goals and knowledge can inform and constrain the solution set in an iterative fashion. The method compares favorably to state of the art XAI tools in a range of quantitative and qualitative comparisons.

Operationalizing Complex Causes: A Pragmatic View of Mediation

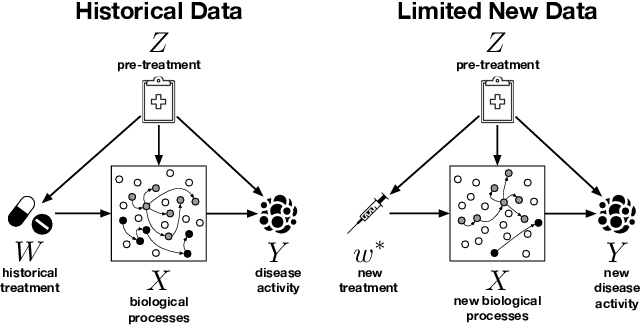
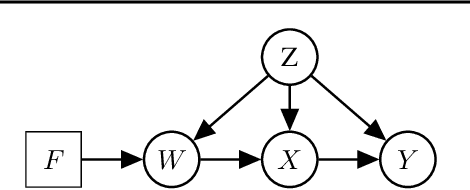
We examine the problem of causal response estimation for complex objects (e.g., text, images, genomics). In this setting, classical \emph{atomic} interventions are often not available (e.g., changes to characters, pixels, DNA base-pairs). Instead, we only have access to indirect or \emph{crude} interventions (e.g., enrolling in a writing program, modifying a scene, applying a gene therapy). In this work, we formalize this problem and provide an initial solution. Given a collection of candidate mediators, we propose (a) a two-step method for predicting the causal responses of crude interventions; and (b) a testing procedure to identify mediators of crude interventions. We demonstrate, on a range of simulated and real-world-inspired examples, that our approach allows us to efficiently estimate the effect of crude interventions with limited data from new treatment regimes.

Testing Conditional Predictive Independence in Supervised Learning Algorithms

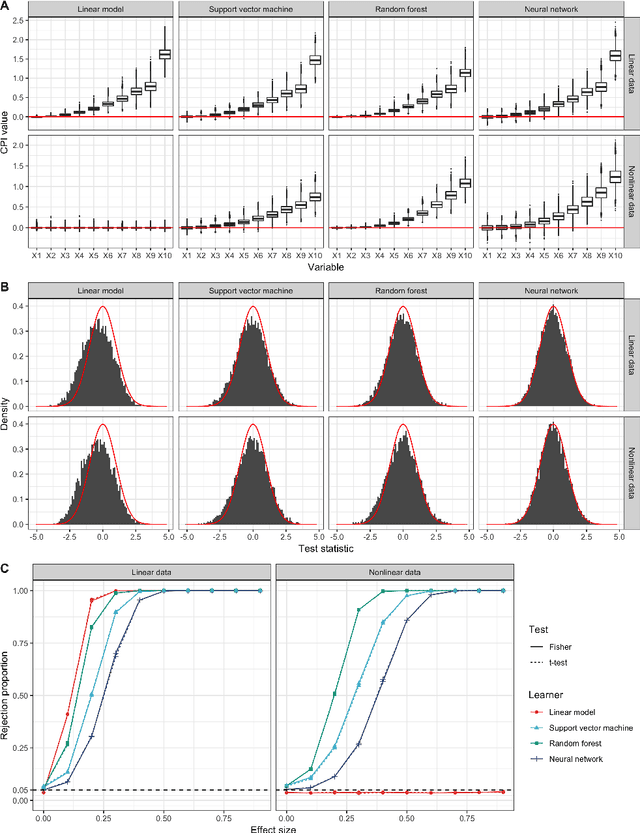
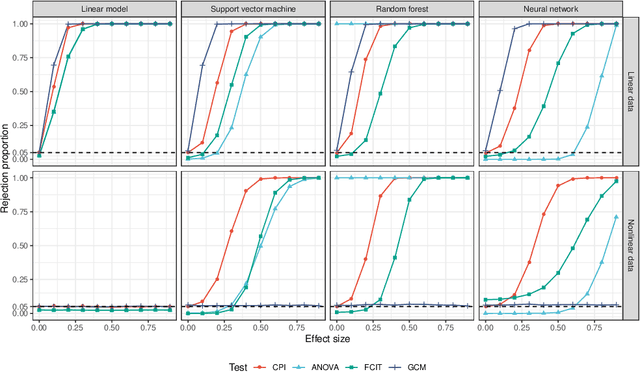
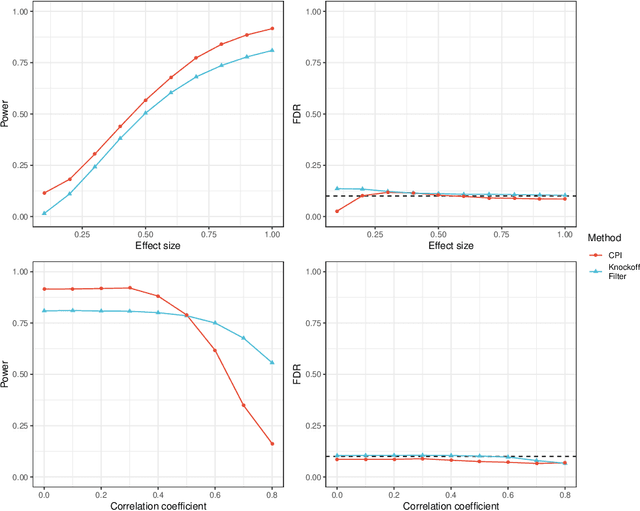
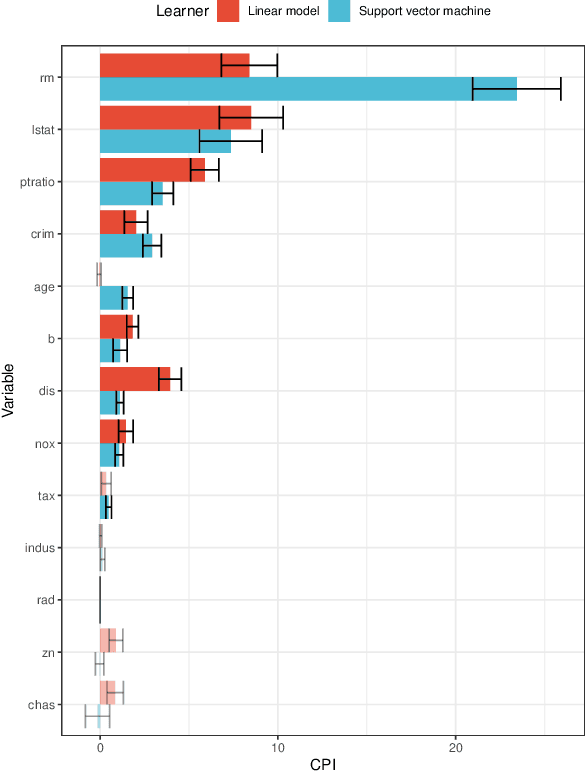
We propose a general test of conditional independence. The conditional predictive impact (CPI) is a provably consistent and unbiased estimator of one or several features' association with a given outcome, conditional on a (potentially empty) reduced feature set. The measure can be calculated using any supervised learning algorithm and loss function. It relies on no parametric assumptions and applies equally well to continuous and categorical predictors and outcomes. The CPI can be efficiently computed for low- or high-dimensional data without any sparsity constraints. We illustrate PAC-Bayesian convergence rates for the CPI and develop statistical inference procedures for evaluating its magnitude, significance, and precision. These tests aid in feature and model selection, extending traditional frequentist and Bayesian techniques to general supervised learning tasks. The CPI may also be used in conjunction with causal discovery algorithms to identify underlying graph structures for multivariate systems. We test our method in conjunction with various algorithms, including linear regression, neural networks, random forests, and support vector machines. Empirical results show that the CPI compares favorably to alternative variable importance measures and other nonparametric tests of conditional independence on a diverse array of real and simulated datasets. Simulations confirm that our inference procedures successfully control Type I error and achieve nominal coverage probability. Our method has been implemented in an R package, cpi, which can be downloaded from https://github.com/dswatson/cpi.