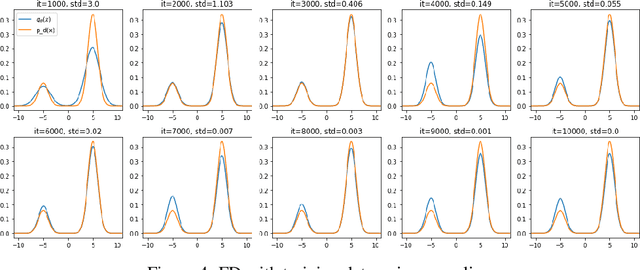
Moment Matching Denoising Gibbs Sampling

Energy-Based Models (EBMs) offer a versatile framework for modeling complex data distributions. However, training and sampling from EBMs continue to pose significant challenges. The widely-used Denoising Score Matching (DSM) method for scalable EBM training suffers from inconsistency issues, causing the energy model to learn a `noisy' data distribution. In this work, we propose an efficient sampling framework: (pseudo)-Gibbs sampling with moment matching, which enables effective sampling from the underlying clean model when given a `noisy' model that has been well-trained via DSM. We explore the benefits of our approach compared to related methods and demonstrate how to scale the method to high-dimensional datasets.

Generalized Multiple Intent Conditioned Slot Filling

Natural language understanding includes the tasks of intent detection (identifying a user's objectives) and slot filling (extracting the entities relevant to those objectives). Prior slot filling methods assume that each intent type cannot occur more than once within a message, however this is often not a valid assumption for real-world settings. In this work, we generalize slot filling by removing the constraint of unique intents in a message. We cast this as a JSON generation task and approach it using a language model. We create a pre-training dataset by combining DBpedia and existing slot filling datasets that we convert for JSON generation. We also generate an in-domain dataset using GPT-3. We train T5 models for this task (with and without exemplars in the prompt) and find that both training datasets improve performance, and that the model is able to generalize to intent types not seen during training.

A hybrid CNN-RNN approach for survival analysis in a Lung Cancer Screening study

In this study, we present a hybrid CNN-RNN approach to investigate long-term survival of subjects in a lung cancer screening study. Subjects who died of cardiovascular and respiratory causes were identified whereby the CNN model was used to capture imaging features in the CT scans and the RNN model was used to investigate time series and thus global information. The models were trained on subjects who underwent cardiovascular and respiratory deaths and a control cohort matched to participant age, gender, and smoking history. The combined model can achieve an AUC of 0.76 which outperforms humans at cardiovascular mortality prediction. The corresponding F1 and Matthews Correlation Coefficient are 0.63 and 0.42 respectively. The generalisability of the model is further validated on an 'external' cohort. The same models were applied to survival analysis with the Cox Proportional Hazard model. It was demonstrated that incorporating the follow-up history can lead to improvement in survival prediction. The Cox neural network can achieve an IPCW C-index of 0.75 on the internal dataset and 0.69 on an external dataset. Delineating imaging features associated with long-term survival can help focus preventative interventions appropriately, particularly for under-recognised pathologies thereby potentially reducing patient morbidity.

Smoothed Q-learning

In Reinforcement Learning the Q-learning algorithm provably converges to the optimal solution. However, as others have demonstrated, Q-learning can also overestimate the values and thereby spend too long exploring unhelpful states. Double Q-learning is a provably convergent alternative that mitigates some of the overestimation issues, though sometimes at the expense of slower convergence. We introduce an alternative algorithm that replaces the max operation with an average, resulting also in a provably convergent off-policy algorithm which can mitigate overestimation yet retain similar convergence as standard Q-learning.

Towards Healing the Blindness of Score Matching

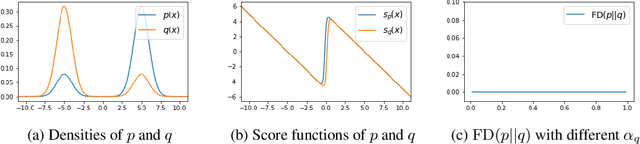
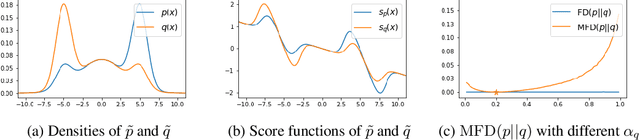
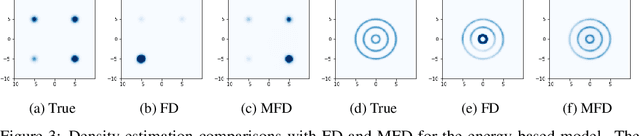
Score-based divergences have been widely used in machine learning and statistics applications. Despite their empirical success, a blindness problem has been observed when using these for multi-modal distributions. In this work, we discuss the blindness problem and propose a new family of divergences that can mitigate the blindness problem. We illustrate our proposed divergence in the context of density estimation and report improved performance compared to traditional approaches.

Integrated Weak Learning

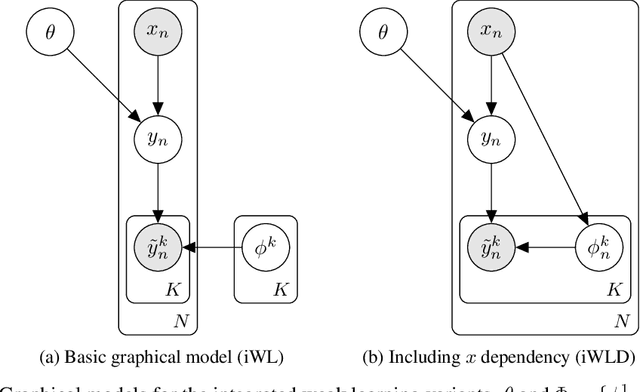
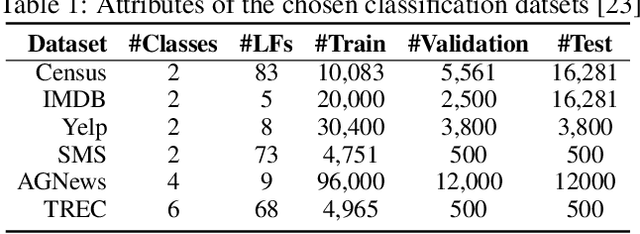
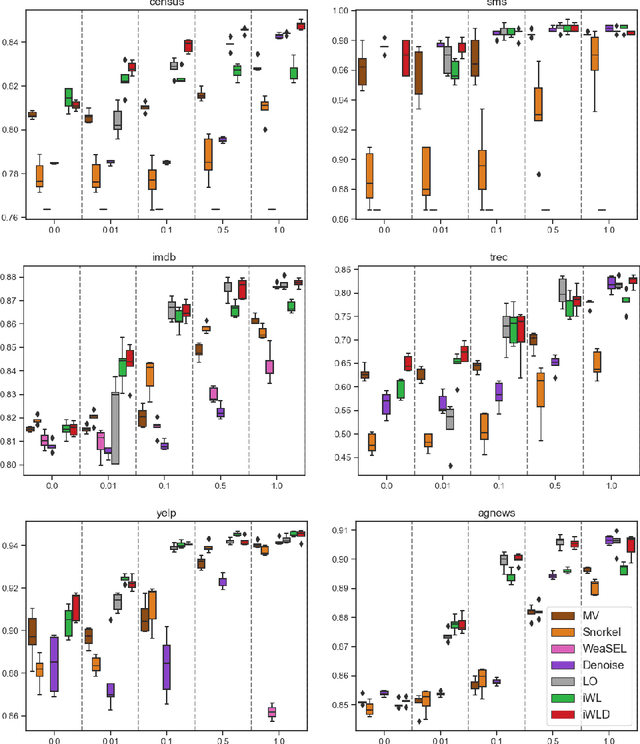
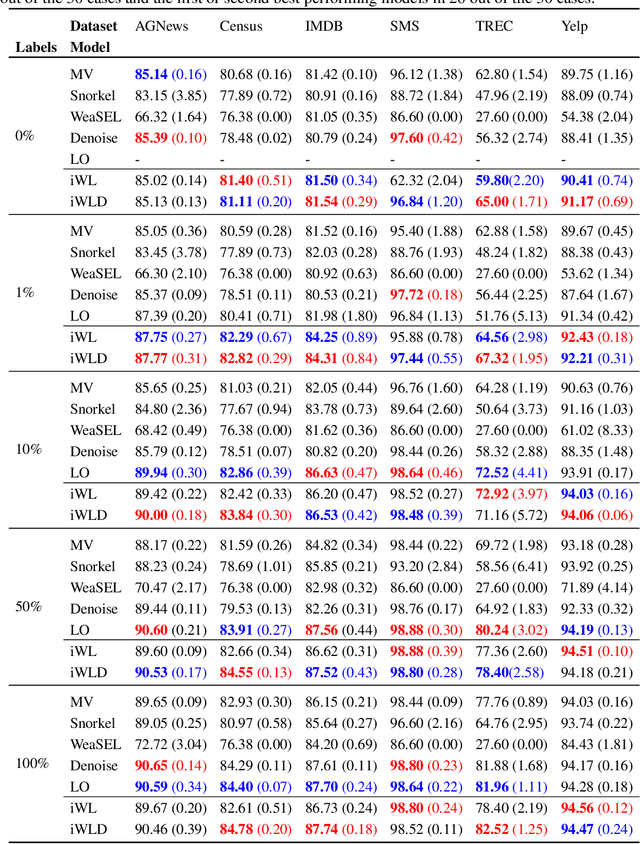
We introduce Integrated Weak Learning, a principled framework that integrates weak supervision into the training process of machine learning models. Our approach jointly trains the end-model and a label model that aggregates multiple sources of weak supervision. We introduce a label model that can learn to aggregate weak supervision sources differently for different datapoints and takes into consideration the performance of the end-model during training. We show that our approach outperforms existing weak learning techniques across a set of 6 benchmark classification datasets. When both a small amount of labeled data and weak supervision are present the increase in performance is both consistent and large, reliably getting a 2-5 point test F1 score gain over non-integrated methods.

Improving VAE-based Representation Learning

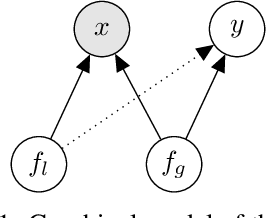
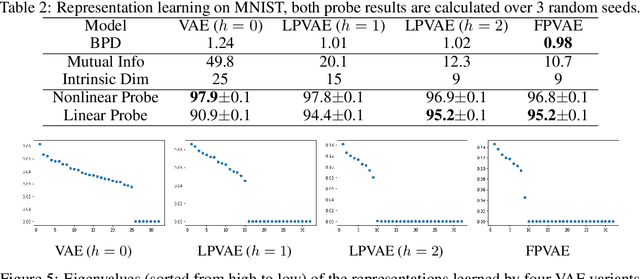
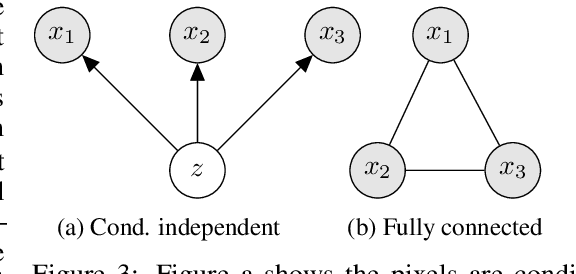
Latent variable models like the Variational Auto-Encoder (VAE) are commonly used to learn representations of images. However, for downstream tasks like semantic classification, the representations learned by VAE are less competitive than other non-latent variable models. This has led to some speculations that latent variable models may be fundamentally unsuitable for representation learning. In this work, we study what properties are required for good representations and how different VAE structure choices could affect the learned properties. We show that by using a decoder that prefers to learn local features, the remaining global features can be well captured by the latent, which significantly improves performance of a downstream classification task. We further apply the proposed model to semi-supervised learning tasks and demonstrate improvements in data efficiency.

Generalization Gap in Amortized Inference

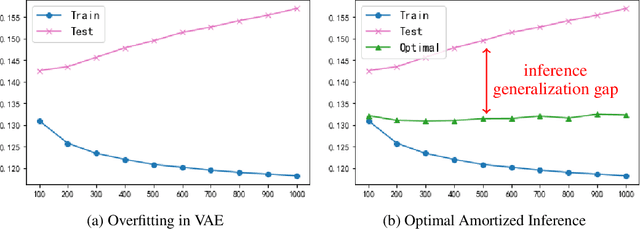
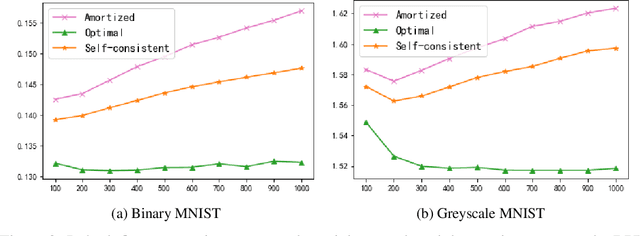
The ability of likelihood-based probabilistic models to generalize to unseen data is central to many machine learning applications such as lossless compression. In this work, we study the generalizations of a popular class of probabilistic models - the Variational Auto-Encoder (VAE). We point out the two generalization gaps that can affect the generalization ability of VAEs and show that the over-fitting phenomenon is usually dominated by the amortized inference network. Based on this observation we propose a new training objective, inspired by the classic wake-sleep algorithm, to improve the generalizations properties of amortized inference. We also demonstrate how it can improve generalization performance in the context of image modeling and lossless compression.

Survival Analysis for Idiopathic Pulmonary Fibrosis using CT Images and Incomplete Clinical Data

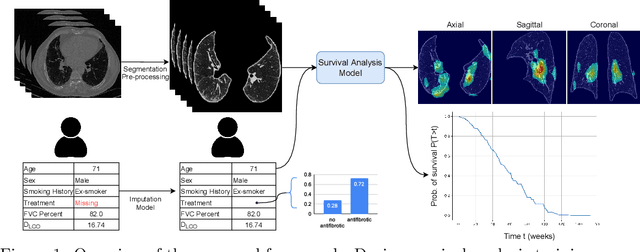
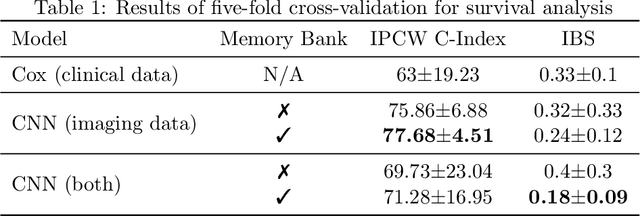
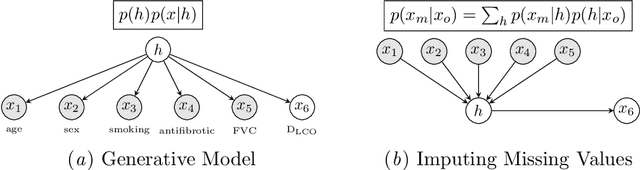
Idiopathic Pulmonary Fibrosis (IPF) is an inexorably progressive fibrotic lung disease with a variable and unpredictable rate of progression. CT scans of the lungs inform clinical assessment of IPF patients and contain pertinent information related to disease progression. In this work, we propose a multi-modal method that uses neural networks and memory banks to predict the survival of IPF patients using clinical and imaging data. The majority of clinical IPF patient records have missing data (e.g. missing lung function tests). To this end, we propose a probabilistic model that captures the dependencies between the observed clinical variables and imputes missing ones. This principled approach to missing data imputation can be naturally combined with a deep survival analysis model. We show that the proposed framework yields significantly better survival analysis results than baselines in terms of concordance index and integrated Brier score. Our work also provides insights into novel image-based biomarkers that are linked to mortality.

Parallel Neural Local Lossless Compression

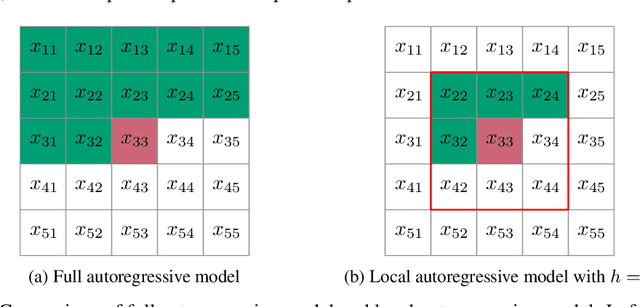
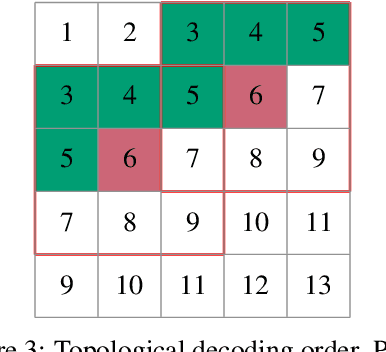
The recently proposed Neural Local Lossless Compression (NeLLoC), which is based on a local autoregressive model, has achieved state-of-the-art (SOTA) out-of-distribution (OOD) generalization performance in the image compression task. In addition to the encouragement of OOD generalization, the local model also allows parallel inference in the decoding stage. In this paper, we propose a parallelization scheme for local autoregressive models. We discuss the practicalities of implementing this scheme, and provide experimental evidence of significant gains in compression runtime compared to the previous, non-parallel implementation.