Mafin: Enhancing Black-Box Embeddings with Model Augmented Fine-Tuning

Retrieval Augmented Generation (RAG) has emerged as an effective solution for mitigating hallucinations in Large Language Models (LLMs). The retrieval stage in RAG typically involves a pre-trained embedding model, which converts queries and passages into vectors to capture their semantics. However, a standard pre-trained embedding model may exhibit sub-optimal performance when applied to specific domain knowledge, necessitating fine-tuning. This paper addresses scenarios where the embeddings are only available from a black-box model. We introduce Model augmented fine-tuning (Mafin) -- a novel approach for fine-tuning a black-box embedding model by augmenting it with a trainable embedding model. Our results demonstrate that Mafin significantly enhances the performance of the black-box embeddings by only requiring the training of a small augmented model. We validate the effectiveness of our method on both labeled and unlabeled datasets, illustrating its broad applicability and efficiency.

Active Preference Learning for Large Language Models

As large language models (LLMs) become more capable, fine-tuning techniques for aligning with human intent are increasingly important. A key consideration for aligning these models is how to most effectively use human resources, or model resources in the case where LLMs themselves are used as oracles. Reinforcement learning from Human or AI preferences (RLHF/RLAIF) is the most prominent example of such a technique, but is complex and often unstable. Direct Preference Optimization (DPO) has recently been proposed as a simpler and more stable alternative. In this work, we develop an active learning strategy for DPO to make better use of preference labels. We propose a practical acquisition function for prompt/completion pairs based on the predictive entropy of the language model and a measure of certainty of the implicit preference model optimized by DPO. We demonstrate how our approach improves both the rate of learning and final performance of fine-tuning on pairwise preference data.

Towards Healing the Blindness of Score Matching

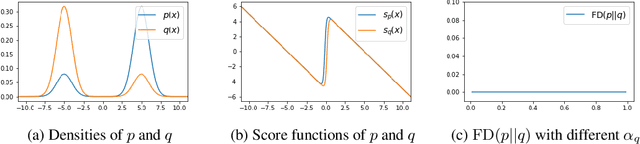
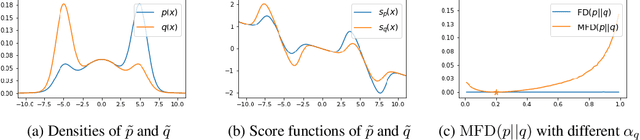
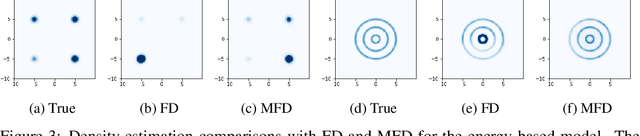
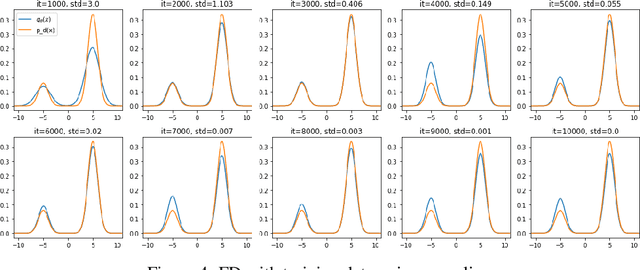
Score-based divergences have been widely used in machine learning and statistics applications. Despite their empirical success, a blindness problem has been observed when using these for multi-modal distributions. In this work, we discuss the blindness problem and propose a new family of divergences that can mitigate the blindness problem. We illustrate our proposed divergence in the context of density estimation and report improved performance compared to traditional approaches.

Integrated Weak Learning

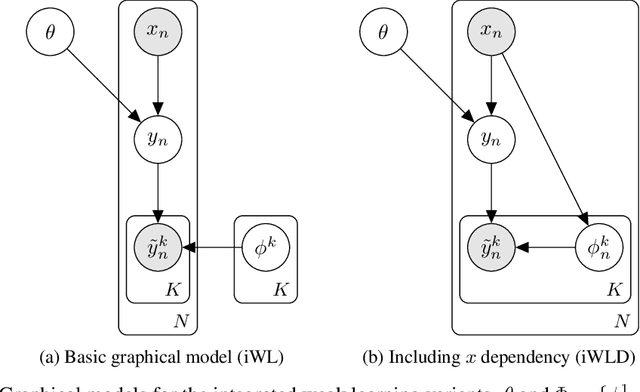
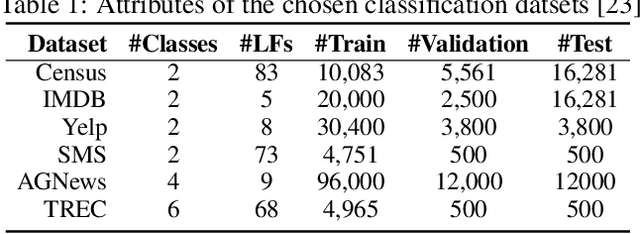
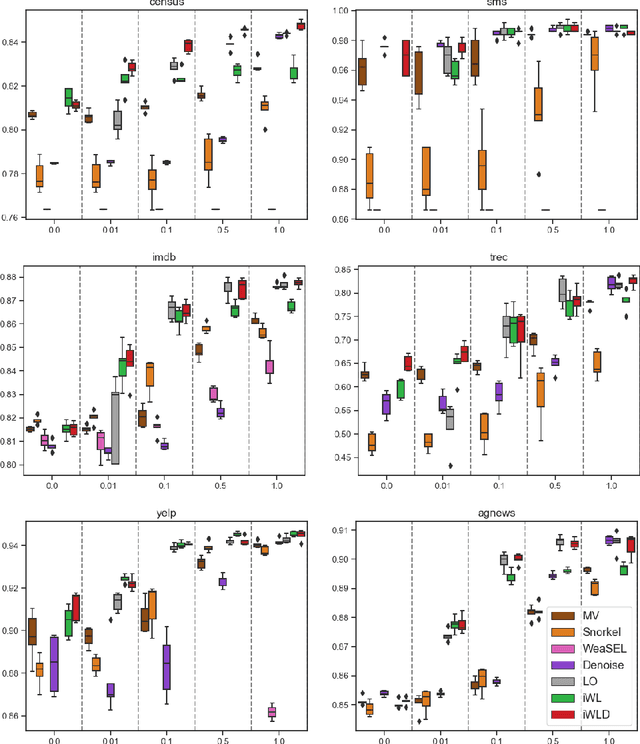
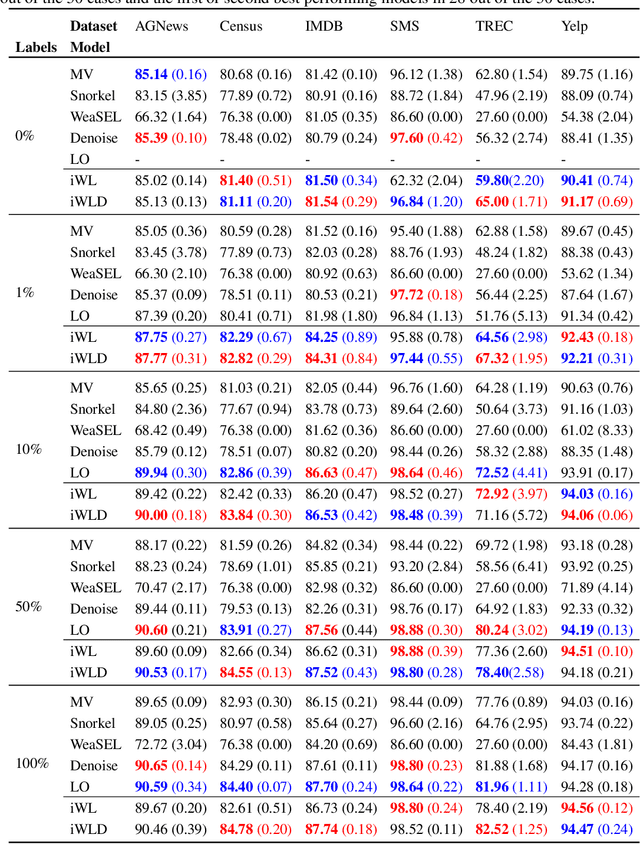
We introduce Integrated Weak Learning, a principled framework that integrates weak supervision into the training process of machine learning models. Our approach jointly trains the end-model and a label model that aggregates multiple sources of weak supervision. We introduce a label model that can learn to aggregate weak supervision sources differently for different datapoints and takes into consideration the performance of the end-model during training. We show that our approach outperforms existing weak learning techniques across a set of 6 benchmark classification datasets. When both a small amount of labeled data and weak supervision are present the increase in performance is both consistent and large, reliably getting a 2-5 point test F1 score gain over non-integrated methods.

Generalization Gap in Amortized Inference

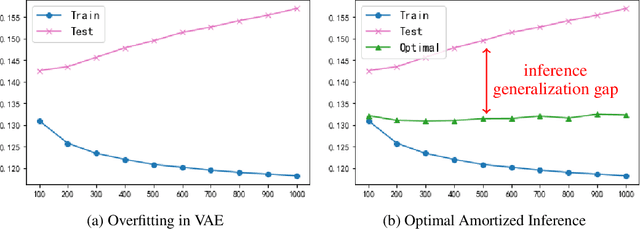
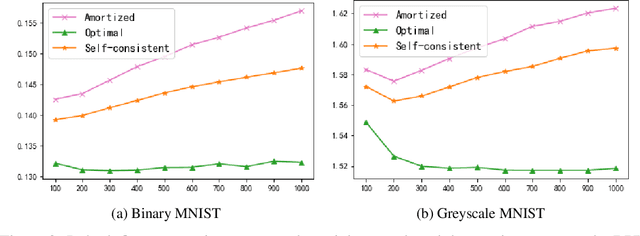
The ability of likelihood-based probabilistic models to generalize to unseen data is central to many machine learning applications such as lossless compression. In this work, we study the generalizations of a popular class of probabilistic models - the Variational Auto-Encoder (VAE). We point out the two generalization gaps that can affect the generalization ability of VAEs and show that the over-fitting phenomenon is usually dominated by the amortized inference network. Based on this observation we propose a new training objective, inspired by the classic wake-sleep algorithm, to improve the generalizations properties of amortized inference. We also demonstrate how it can improve generalization performance in the context of image modeling and lossless compression.

Sample Efficient Model Evaluation

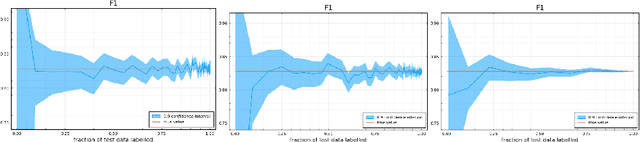
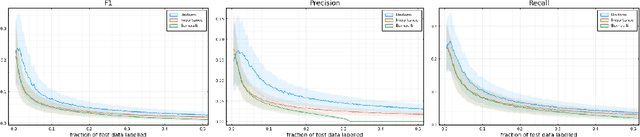
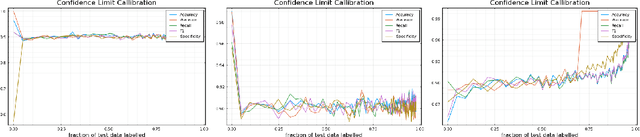
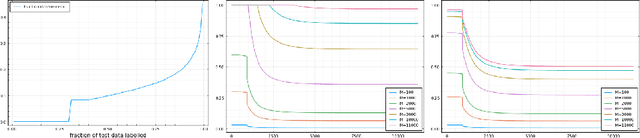
Labelling data is a major practical bottleneck in training and testing classifiers. Given a collection of unlabelled data points, we address how to select which subset to label to best estimate test metrics such as accuracy, $F_1$ score or micro/macro $F_1$. We consider two sampling based approaches, namely the well-known Importance Sampling and we introduce a novel application of Poisson Sampling. For both approaches we derive the minimal error sampling distributions and how to approximate and use them to form estimators and confidence intervals. We show that Poisson Sampling outperforms Importance Sampling both theoretically and experimentally.

Estimating the Uncertainty of Neural Network Forecasts for Influenza Prevalence Using Web Search Activity

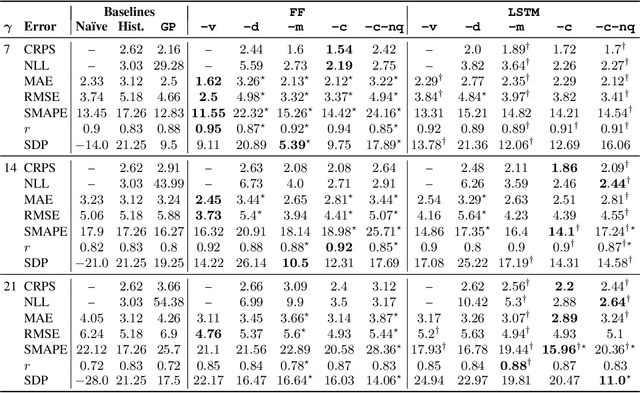
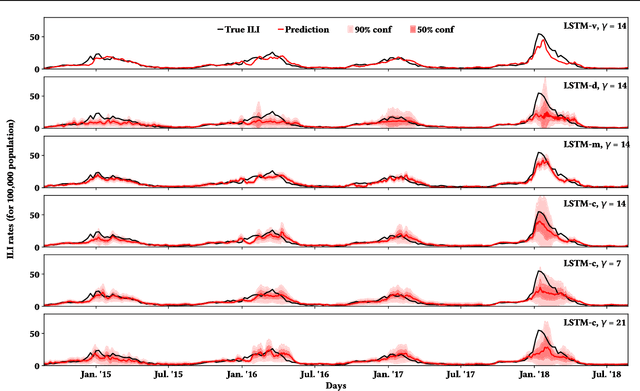
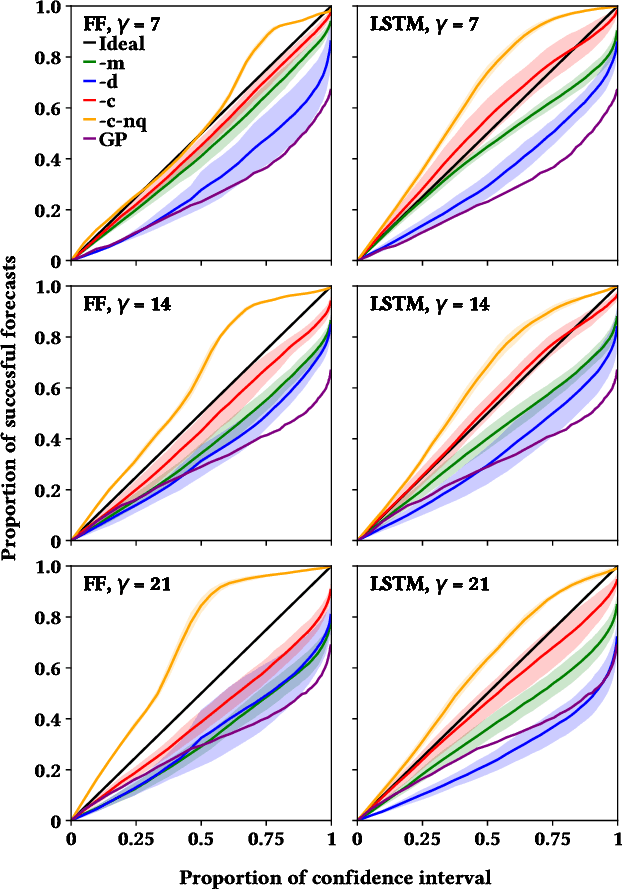
Influenza is an infectious disease with the potential to become a pandemic, and hence, forecasting its prevalence is an important undertaking for planning an effective response. Research has found that web search activity can be used to improve influenza models. Neural networks (NN) can provide state-of-the-art forecasting accuracy but do not commonly incorporate uncertainty in their estimates, something essential for using them effectively during decision making. In this paper, we demonstrate how Bayesian Neural Networks (BNNs) can be used to both provide a forecast and a corresponding uncertainty without significant loss in forecasting accuracy compared to traditional NNs. Our method accounts for two sources of uncertainty: data and model uncertainty, arising due to measurement noise and model specification, respectively. Experiments are conducted using 14 years of data for England, assessing the model's accuracy over the last 4 flu seasons in this dataset. We evaluate the performance of different models including competitive baselines with conventional metrics as well as error functions that incorporate uncertainty estimates. Our empirical analysis indicates that considering both sources of uncertainty simultaneously is superior to considering either one separately. We also show that a BNN with recurrent layers that models both sources of uncertainty yields superior accuracy for these metrics for forecasting horizons greater than 7 days.