Provable Privacy Attacks on Trained Shallow Neural Networks

We study what provable privacy attacks can be shown on trained, 2-layer ReLU neural networks. We explore two types of attacks; data reconstruction attacks, and membership inference attacks. We prove that theoretical results on the implicit bias of 2-layer neural networks can be used to provably reconstruct a set of which at least a constant fraction are training points in a univariate setting, and can also be used to identify with high probability whether a given point was used in the training set in a high dimensional setting. To the best of our knowledge, our work is the first to show provable vulnerabilities in this setting.

Depth Separations in Neural Networks: Separating the Dimension from the Accuracy

We prove an exponential separation between depth 2 and depth 3 neural networks, when approximating an $\mathcal{O}(1)$-Lipschitz target function to constant accuracy, with respect to a distribution with support in $[0,1]^{d}$, assuming exponentially bounded weights. This addresses an open problem posed in \citet{safran2019depth}, and proves that the curse of dimensionality manifests in depth 2 approximation, even in cases where the target function can be represented efficiently using depth 3. Previously, lower bounds that were used to separate depth 2 from depth 3 required that at least one of the Lipschitz parameter, target accuracy or (some measure of) the size of the domain of approximation scale polynomially with the input dimension, whereas we fix the former two and restrict our domain to the unit hypercube. Our lower bound holds for a wide variety of activation functions, and is based on a novel application of an average- to worst-case random self-reducibility argument, to reduce the problem to threshold circuits lower bounds.

How Many Neurons Does it Take to Approximate the Maximum?

We study the size of a neural network needed to approximate the maximum function over $d$ inputs, in the most basic setting of approximating with respect to the $L_2$ norm, for continuous distributions, for a network that uses ReLU activations. We provide new lower and upper bounds on the width required for approximation across various depths. Our results establish new depth separations between depth 2 and 3, and depth 3 and 5 networks, as well as providing a depth $\mathcal{O}(\log(\log(d)))$ and width $\mathcal{O}(d)$ construction which approximates the maximum function, significantly improving upon the depth requirements of the best previously known bounds for networks with linearly-bounded width. Our depth separation results are facilitated by a new lower bound for depth 2 networks approximating the maximum function over the uniform distribution, assuming an exponential upper bound on the size of the weights. Furthermore, we are able to use this depth 2 lower bound to provide tight bounds on the number of neurons needed to approximate the maximum by a depth 3 network. Our lower bounds are of potentially broad interest as they apply to the widely studied and used \emph{max} function, in contrast to many previous results that base their bounds on specially constructed or pathological functions and distributions.

On the Effective Number of Linear Regions in Shallow Univariate ReLU Networks: Convergence Guarantees and Implicit Bias

We study the dynamics and implicit bias of gradient flow (GF) on univariate ReLU neural networks with a single hidden layer in a binary classification setting. We show that when the labels are determined by the sign of a target network with $r$ neurons, with high probability over the initialization of the network and the sampling of the dataset, GF converges in direction (suitably defined) to a network achieving perfect training accuracy and having at most $\mathcal{O}(r)$ linear regions, implying a generalization bound. Our result may already hold for mild over-parameterization, where the width is $\tilde{\mathcal{O}}(r)$ and independent of the sample size.

Optimization-Based Separations for Neural Networks

Depth separation results propose a possible theoretical explanation for the benefits of deep neural networks over shallower architectures, establishing that the former possess superior approximation capabilities. However, there are no known results in which the deeper architecture leverages this advantage into a provable optimization guarantee. We prove that when the data are generated by a distribution with radial symmetry which satisfies some mild assumptions, gradient descent can efficiently learn ball indicator functions using a depth 2 neural network with two layers of sigmoidal activations, and where the hidden layer is held fixed throughout training. Since it is known that ball indicators are hard to approximate with respect to a certain heavy-tailed distribution when using depth 2 networks with a single layer of non-linearities (Safran and Shamir, 2017), this establishes what is to the best of our knowledge, the first optimization-based separation result where the approximation benefits of the stronger architecture provably manifest in practice. Our proof technique relies on a random features approach which reduces the problem to learning with a single neuron, where new tools are required to show the convergence of gradient descent when the distribution of the data is heavy-tailed.

Random Shuffling Beats SGD Only After Many Epochs on Ill-Conditioned Problems

Recently, there has been much interest in studying the convergence rates of without-replacement SGD, and proving that it is faster than with-replacement SGD in the worst case. However, these works ignore or do not provide tight bounds in terms of the problem's geometry, including its condition number. Perhaps surprisingly, we prove that when the condition number is taken into account, without-replacement SGD \emph{does not} significantly improve on with-replacement SGD in terms of worst-case bounds, unless the number of epochs (passes over the data) is larger than the condition number. Since many problems in machine learning and other areas are both ill-conditioned and involve large datasets, this indicates that without-replacement does not necessarily improve over with-replacement sampling for realistic iteration budgets. We show this by providing new lower and upper bounds which are tight (up to log factors), for quadratic problems with commuting quadratic terms, precisely quantifying the dependence on the problem parameters.

The Effects of Mild Over-parameterization on the Optimization Landscape of Shallow ReLU Neural Networks

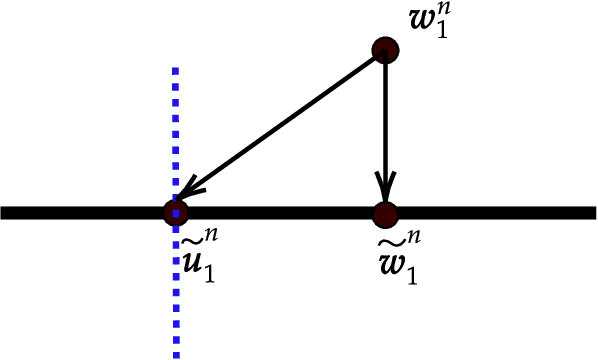
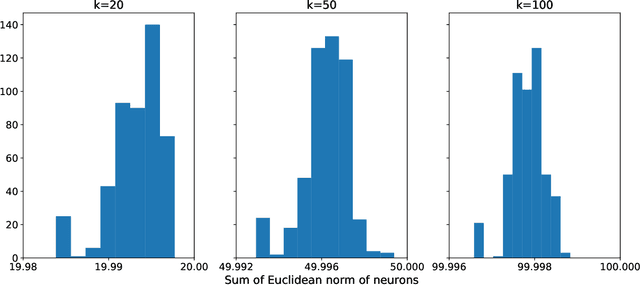
We study the effects of mild over-parameterization on the optimization landscape of a simple ReLU neural network of the form $\mathbf{x}\mapsto\sum_{i=1}^k\max\{0,\mathbf{w}_i^{\top}\mathbf{x}\}$, in a well-studied teacher-student setting where the target values are generated by the same architecture, and when directly optimizing over the population squared loss with respect to Gaussian inputs. We prove that while the objective is strongly convex around the global minima when the teacher and student networks possess the same number of neurons, it is not even \emph{locally convex} after any amount of over-parameterization. Moreover, related desirable properties (e.g., one-point strong convexity and the Polyak-{\L}ojasiewicz condition) also do not hold even locally. On the other hand, we establish that the objective remains one-point strongly convex in \emph{most} directions (suitably defined). For the non-global minima, we prove that adding even just a single neuron will turn a non-global minimum into a saddle point. This holds under some technical conditions which we validate empirically. These results provide a possible explanation for why recovering a global minimum becomes significantly easier when we over-parameterize, even if the amount of over-parameterization is very moderate.

How Good is SGD with Random Shuffling?

We study the performance of stochastic gradient descent (SGD) on smooth and strongly-convex finite-sum optimization problems. In contrast to the majority of existing theoretical works, which assume that individual functions are sampled with replacement, we focus here on popular but poorly-understood heuristics, which involve going over random permutations of the individual functions. This setting has been investigated in several recent works, but the optimal error rates remains unclear. In this paper, we provide lower bounds on the expected optimization error with these heuristics (using SGD with any constant step size), which elucidate their advantages and disadvantages. In particular, we prove that after $k$ passes over $n$ individual functions, if the functions are re-shuffled after every pass, the best possible optimization error for SGD is at least $\Omega\left(1/(nk)^2+1/nk^3\right)$, which partially corresponds to recently derived upper bounds, and we conjecture to be tight. Moreover, if the functions are only shuffled once, then the lower bound increases to $\Omega(1/nk^2)$. Since there are strictly smaller upper bounds for random reshuffling, this proves an inherent performance gap between SGD with single shuffling and repeated shuffling. As a more minor contribution, we also provide a non-asymptotic $\Omega(1/k^2)$ lower bound (independent of $n$) for cyclic gradient descent, where no random shuffling takes place.

Depth Separations in Neural Networks: What is Actually Being Separated?

Existing depth separation results for constant-depth networks essentially show that certain radial functions in $\mathbb{R}^d$, which can be easily approximated with depth $3$ networks, cannot be approximated by depth $2$ networks, even up to constant accuracy, unless their size is exponential in $d$. However, the functions used to demonstrate this are rapidly oscillating, with a Lipschitz parameter scaling polynomially with the dimension $d$ (or equivalently, by scaling the function, the hardness result applies to $\mathcal{O}(1)$-Lipschitz functions only when the target accuracy $\epsilon$ is at most $\text{poly}(1/d)$). In this paper, we study whether such depth separations might still hold in the natural setting of $\mathcal{O}(1)$-Lipschitz radial functions, when $\epsilon$ does not scale with $d$. Perhaps surprisingly, we show that the answer is negative: In contrast to the intuition suggested by previous work, it \emph{is} possible to approximate $\mathcal{O}(1)$-Lipschitz radial functions with depth $2$, size $\text{poly}(d)$ networks, for every constant $\epsilon$. We complement it by showing that approximating such functions is also possible with depth $2$, size $\text{poly}(1/\epsilon)$ networks, for every constant $d$. Finally, we show that it is not possible to have polynomial dependence in both $d,1/\epsilon$ simultaneously. Overall, our results indicate that in order to show depth separations for expressing $\mathcal{O}(1)$-Lipschitz functions with constant accuracy -- if at all possible -- one would need fundamentally different techniques than existing ones in the literature.

A Simple Explanation for the Existence of Adversarial Examples with Small Hamming Distance

The existence of adversarial examples in which an imperceptible change in the input can fool well trained neural networks was experimentally discovered by Szegedy et al in 2013, who called them "Intriguing properties of neural networks". Since then, this topic had become one of the hottest research areas within machine learning, but the ease with which we can switch between any two decisions in targeted attacks is still far from being understood, and in particular it is not clear which parameters determine the number of input coordinates we have to change in order to mislead the network. In this paper we develop a simple mathematical framework which enables us to think about this baffling phenomenon from a fresh perspective, turning it into a natural consequence of the geometry of $\mathbb{R}^n$ with the $L_0$ (Hamming) metric, which can be quantitatively analyzed. In particular, we explain why we should expect to find targeted adversarial examples with Hamming distance of roughly $m$ in arbitrarily deep neural networks which are designed to distinguish between $m$ input classes.