Generalized Linear Models with 1-Bit Measurements: Asymptotics of the Maximum Likelihood Estimator

This work establishes regularity conditions for consistency and asymptotic normality of the multiple parameter maximum likelihood estimator(MLE) from censored data, where the censoring mechanism is in the form of $1$-bit measurements. The underlying distribution of the uncensored data is assumed to belong to the exponential family, with natural parameters expressed as a linear combination of the predictors, known as generalized linear model (GLM). As part of the analysis, the Fisher information matrix is also derived for both censored and uncensored data, which helps to quantify the impact of censoring and assess the performance of the MLE. The choice of GLM allows one to consider a variety of practical examples where 1-bit estimation is of interest. In particular, it is shown how the derived results can be used to analyze two practically relevant scenarios: the Gaussian model with both unknown mean and variance, and the Poisson model with an unknown mean.

Max-sliced Wasserstein concentration and uniform ratio bounds of empirical measures on RKHS

Optimal transport and the Wasserstein distance $\mathcal{W}_p$ have recently seen a number of applications in the fields of statistics, machine learning, data science, and the physical sciences. These applications are however severely restricted by the curse of dimensionality, meaning that the number of data points needed to estimate these problems accurately increases exponentially in the dimension. To alleviate this problem, a number of variants of $\mathcal{W}_p$ have been introduced. We focus here on one of these variants, namely the max-sliced Wasserstein metric $\overline{\mathcal{W}}_p$. This metric reduces the high-dimensional minimization problem given by $\mathcal{W}_p$ to a maximum of one-dimensional measurements in an effort to overcome the curse of dimensionality. In this note we derive concentration results and upper bounds on the expectation of $\overline{\mathcal{W}}_p$ between the true and empirical measure on unbounded reproducing kernel Hilbert spaces. We show that, under quite generic assumptions, probability measures concentrate uniformly fast in one-dimensional subspaces, at (nearly) parametric rates. Our results rely on an improvement of currently known bounds for $\overline{\mathcal{W}}_p$ in the finite-dimensional case.

Is it easier to count communities than find them?

Random graph models with community structure have been studied extensively in the literature. For both the problems of detecting and recovering community structure, an interesting landscape of statistical and computational phase transitions has emerged. A natural unanswered question is: might it be possible to infer properties of the community structure (for instance, the number and sizes of communities) even in situations where actually finding those communities is believed to be computationally hard? We show the answer is no. In particular, we consider certain hypothesis testing problems between models with different community structures, and we show (in the low-degree polynomial framework) that testing between two options is as hard as finding the communities. In addition, our methods give the first computational lower bounds for testing between two different `planted' distributions, whereas previous results have considered testing between a planted distribution and an i.i.d. `null' distribution.

Entropic CLT for Order Statistics

It is well known that central order statistics exhibit a central limit behavior and converge to a Gaussian distribution as the sample size grows. This paper strengthens this known result by establishing an entropic version of the CLT that ensures a stronger mode of convergence using the relative entropy. In particular, an order $O(1/\sqrt{n})$ rate of convergence is established under mild conditions on the parent distribution of the sample generating the order statistics. To prove this result, ancillary results on order statistics are derived, which might be of independent interest.

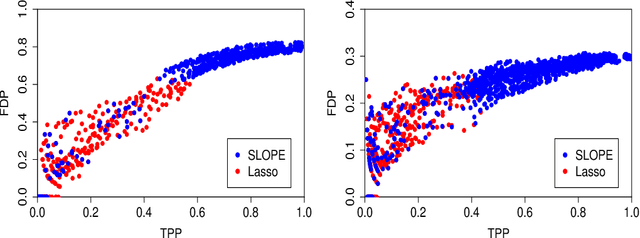
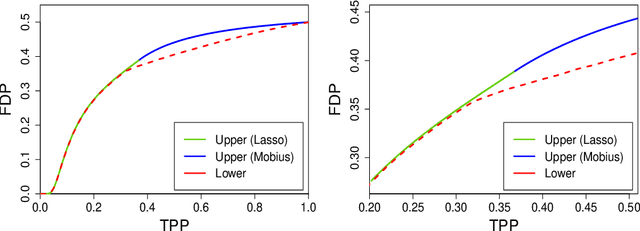
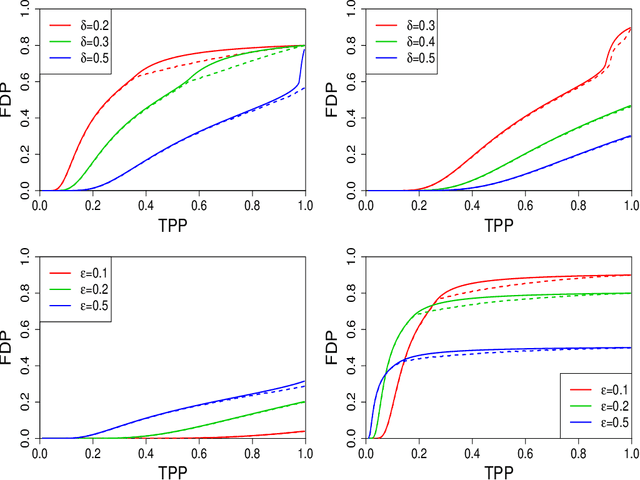
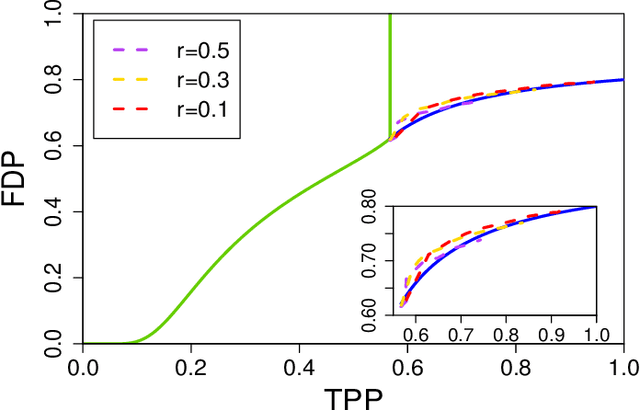
Characterizing the SLOPE Trade-off: A Variational Perspective and the Donoho-Tanner Limit

Sorted l1 regularization has been incorporated into many methods for solving high-dimensional statistical estimation problems, including the SLOPE estimator in linear regression. In this paper, we study how this relatively new regularization technique improves variable selection by characterizing the optimal SLOPE trade-off between the false discovery proportion (FDP) and true positive proportion (TPP) or, equivalently, between measures of type I error and power. Assuming a regime of linear sparsity and working under Gaussian random designs, we obtain an upper bound on the optimal trade-off for SLOPE, showing its capability of breaking the Donoho-Tanner power limit. To put it into perspective, this limit is the highest possible power that the Lasso, which is perhaps the most popular l1-based method, can achieve even with arbitrarily strong effect sizes. Next, we derive a tight lower bound that delineates the fundamental limit of sorted l1 regularization in optimally trading the FDP off for the TPP. Finally, we show that on any problem instance, SLOPE with a certain regularization sequence outperforms the Lasso, in the sense of having a smaller FDP, larger TPP and smaller l2 estimation risk simultaneously. Our proofs are based on a novel technique that reduces a variational calculus problem to a class of infinite-dimensional convex optimization problems and a very recent result from approximate message passing theory.

A unifying tutorial on Approximate Message Passing

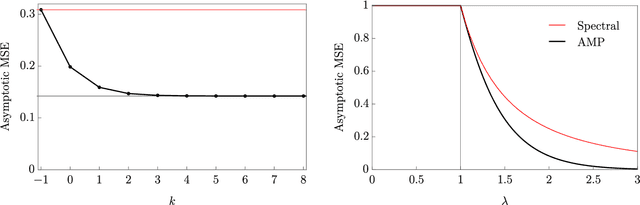
Over the last decade or so, Approximate Message Passing (AMP) algorithms have become extremely popular in various structured high-dimensional statistical problems. The fact that the origins of these techniques can be traced back to notions of belief propagation in the statistical physics literature lends a certain mystique to the area for many statisticians. Our goal in this work is to present the main ideas of AMP from a statistical perspective, to illustrate the power and flexibility of the AMP framework. Along the way, we strengthen and unify many of the results in the existing literature.

On the Robustness to Misspecification of $α$-Posteriors and Their Variational Approximations

$\alpha$-posteriors and their variational approximations distort standard posterior inference by downweighting the likelihood and introducing variational approximation errors. We show that such distortions, if tuned appropriately, reduce the Kullback-Leibler (KL) divergence from the true, but perhaps infeasible, posterior distribution when there is potential parametric model misspecification. To make this point, we derive a Bernstein-von Mises theorem showing convergence in total variation distance of $\alpha$-posteriors and their variational approximations to limiting Gaussian distributions. We use these distributions to evaluate the KL divergence between true and reported posteriors. We show this divergence is minimized by choosing $\alpha$ strictly smaller than one, assuming there is a vanishingly small probability of model misspecification. The optimized value becomes smaller as the the misspecification becomes more severe. The optimized KL divergence increases logarithmically in the degree of misspecification and not linearly as with the usual posterior.

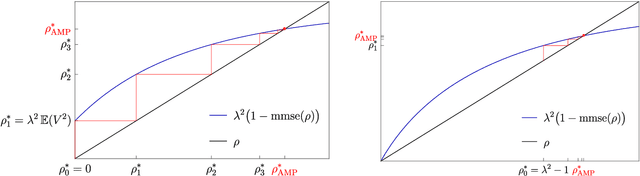
All-or-nothing statistical and computational phase transitions in sparse spiked matrix estimation

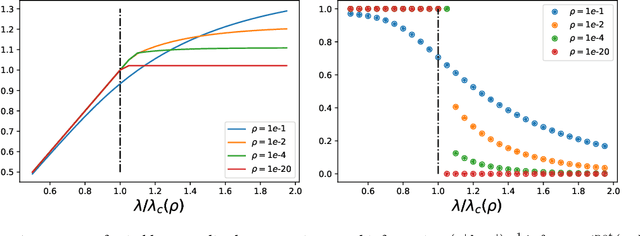
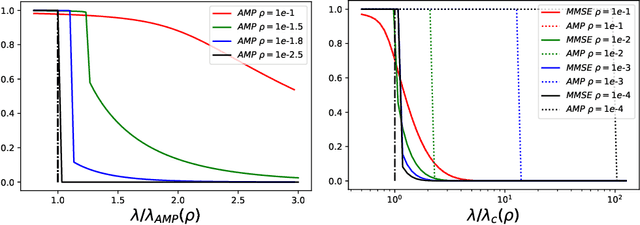
We determine statistical and computational limits for estimation of a rank-one matrix (the spike) corrupted by an additive gaussian noise matrix, in a sparse limit, where the underlying hidden vector (that constructs the rank-one matrix) has a number of non-zero components that scales sub-linearly with the total dimension of the vector, and the signal-to-noise ratio tends to infinity at an appropriate speed. We prove explicit low-dimensional variational formulas for the asymptotic mutual information between the spike and the observed noisy matrix and analyze the approximate message passing algorithm in the sparse regime. For Bernoulli and Bernoulli-Rademacher distributed vectors, and when the sparsity and signal strength satisfy an appropriate scaling relation, we find all-or-nothing phase transitions for the asymptotic minimum and algorithmic mean-square errors. These jump from their maximum possible value to zero, at well defined signal-to-noise thresholds whose asymptotic values we determine exactly. In the asymptotic regime the statistical-to-algorithmic gap diverges indicating that sparse recovery is hard for approximate message passing.

Rigorous State Evolution Analysis for Approximate Message Passing with Side Information

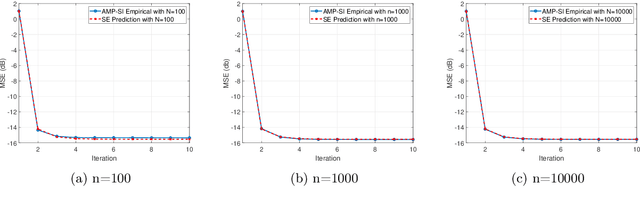
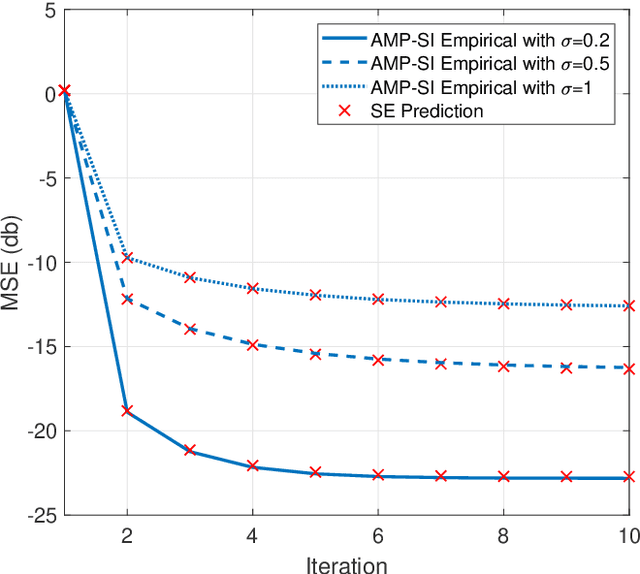
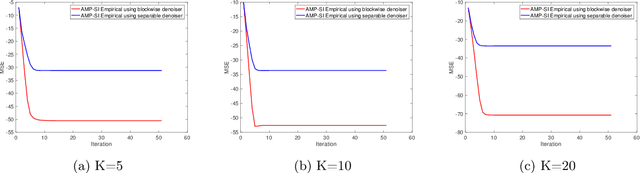
A common goal in many research areas is to reconstruct an unknown signal x from noisy linear measurements. Approximate message passing (AMP) is a class of low-complexity algorithms that can be used for efficiently solving such high-dimensional regression tasks. Often, it is the case that side information (SI) is available during reconstruction. For this reason, a novel algorithmic framework that incorporates SI into AMP, referred to as approximate message passing with side information (AMP-SI), has been recently introduced. In this work, we provide rigorous performance guarantees for AMP-SI when there are statistical dependencies between the signal and SI pairs and the entries of the measurement matrix are independent and identically distributed Gaussian. The AMP-SI performance is shown to be provably tracked by a scalar iteration referred to as state evolution. Moreover, we provide numerical examples that demonstrate empirically that the SE can predict the AMP-SI mean square error accurately.

Algorithmic Analysis and Statistical Estimation of SLOPE via Approximate Message Passing

SLOPE is a relatively new convex optimization procedure for high-dimensional linear regression via the sorted l1 penalty: the larger the rank of the fitted coefficient, the larger the penalty. This non-separable penalty renders many existing techniques invalid or inconclusive in analyzing the SLOPE solution. In this paper, we develop an asymptotically exact characterization of the SLOPE solution under Gaussian random designs through solving the SLOPE problem using approximate message passing (AMP). This algorithmic approach allows us to approximate the SLOPE solution via the much more amenable AMP iterates. Explicitly, we characterize the asymptotic dynamics of the AMP iterates relying on a recently developed state evolution analysis for non-separable penalties, thereby overcoming the difficulty caused by the sorted l1 penalty. Moreover, we prove that the AMP iterates converge to the SLOPE solution in an asymptotic sense, and numerical simulations show that the convergence is surprisingly fast. Our proof rests on a novel technique that specifically leverages the SLOPE problem. In contrast to prior literature, our work not only yields an asymptotically sharp analysis but also offers an algorithmic, flexible, and constructive approach to understanding the SLOPE problem.