Stochastic Gradient Flow Dynamics of Test Risk and its Exact Solution for Weak Features

We investigate the test risk of continuous-time stochastic gradient flow dynamics in learning theory. Using a path integral formulation we provide, in the regime of a small learning rate, a general formula for computing the difference between test risk curves of pure gradient and stochastic gradient flows. We apply the general theory to a simple model of weak features, which displays the double descent phenomenon, and explicitly compute the corrections brought about by the added stochastic term in the dynamics, as a function of time and model parameters. The analytical results are compared to simulations of discrete-time stochastic gradient descent and show good agreement.

Gradient flow on extensive-rank positive semi-definite matrix denoising

In this work, we present a new approach to analyze the gradient flow for a positive semi-definite matrix denoising problem in an extensive-rank and high-dimensional regime. We use recent linear pencil techniques of random matrix theory to derive fixed point equations which track the complete time evolution of the matrix-mean-square-error of the problem. The predictions of the resulting fixed point equations are validated by numerical experiments. In this short note we briefly illustrate a few predictions of our formalism by way of examples, and in particular we uncover continuous phase transitions in the extensive-rank and high-dimensional regime, which connect to the classical phase transitions of the low-rank problem in the appropriate limit. The formalism has much wider applicability than shown in this communication.

Gradient flow in the gaussian covariate model: exact solution of learning curves and multiple descent structures

A recent line of work has shown remarkable behaviors of the generalization error curves in simple learning models. Even the least-squares regression has shown atypical features such as the model-wise double descent, and further works have observed triple or multiple descents. Another important characteristic are the epoch-wise descent structures which emerge during training. The observations of model-wise and epoch-wise descents have been analytically derived in limited theoretical settings (such as the random feature model) and are otherwise experimental. In this work, we provide a full and unified analysis of the whole time-evolution of the generalization curve, in the asymptotic large-dimensional regime and under gradient-flow, within a wider theoretical setting stemming from a gaussian covariate model. In particular, we cover most cases already disparately observed in the literature, and also provide examples of the existence of multiple descent structures as a function of a model parameter or time. Furthermore, we show that our theoretical predictions adequately match the learning curves obtained by gradient descent over realistic datasets. Technically we compute averages of rational expressions involving random matrices using recent developments in random matrix theory based on "linear pencils". Another contribution, which is also of independent interest in random matrix theory, is a new derivation of related fixed point equations (and an extension there-off) using Dyson brownian motions.

Model, sample, and epoch-wise descents: exact solution of gradient flow in the random feature model

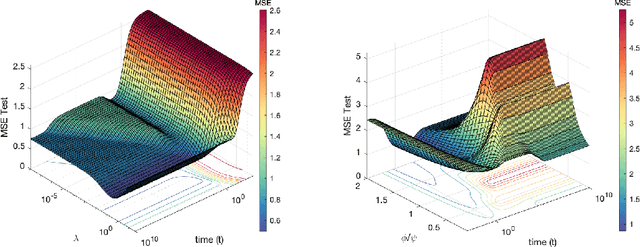
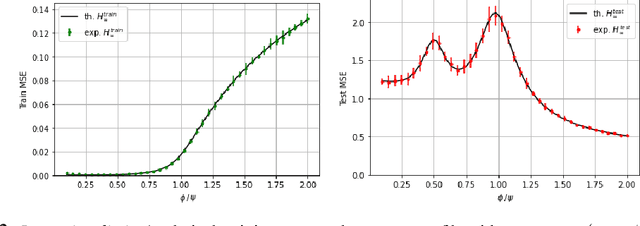
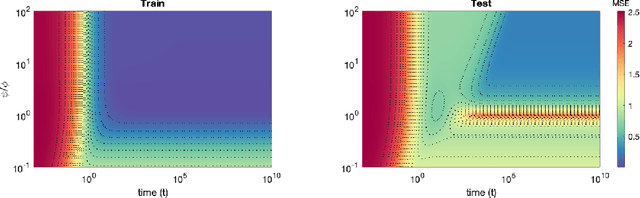
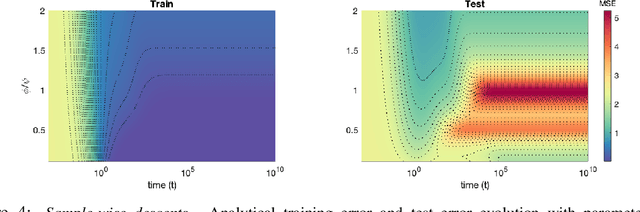
Recent evidence has shown the existence of a so-called double-descent and even triple-descent behavior for the generalization error of deep-learning models. This important phenomenon commonly appears in implemented neural network architectures, and also seems to emerge in epoch-wise curves during the training process. A recent line of research has highlighted that random matrix tools can be used to obtain precise analytical asymptotics of the generalization (and training) errors of the random feature model. In this contribution, we analyze the whole temporal behavior of the generalization and training errors under gradient flow for the random feature model. We show that in the asymptotic limit of large system size the full time-evolution path of both errors can be calculated analytically. This allows us to observe how the double and triple descents develop over time, if and when early stopping is an option, and also observe time-wise descent structures. Our techniques are based on Cauchy complex integral representations of the errors together with recent random matrix methods based on linear pencils.

Statistical limits of dictionary learning: random matrix theory and the spectral replica method

We consider increasingly complex models of matrix denoising and dictionary learning in the Bayes-optimal setting, in the challenging regime where the matrices to infer have a rank growing linearly with the system size. This is in contrast with most existing literature concerned with the low-rank (i.e., constant-rank) regime. We first consider a class of rotationally invariant matrix denoising problems whose mutual information and minimum mean-square error are computable using standard techniques from random matrix theory. Next, we analyze the more challenging models of dictionary learning. To do so we introduce a novel combination of the replica method from statistical mechanics together with random matrix theory, coined spectral replica method. It allows us to conjecture variational formulas for the mutual information between hidden representations and the noisy data as well as for the overlaps quantifying the optimal reconstruction error. The proposed methods reduce the number of degrees of freedom from $\Theta(N^2)$ (matrix entries) to $\Theta(N)$ (eigenvalues or singular values), and yield Coulomb gas representations of the mutual information which are reminiscent of matrix models in physics. The main ingredients are the use of HarishChandra-Itzykson-Zuber spherical integrals combined with a new replica symmetric decoupling ansatz at the level of the probability distributions of eigenvalues (or singular values) of certain overlap matrices.

Mismatched Estimation of rank-one symmetric matrices under Gaussian noise

We consider the estimation of an n-dimensional vector s from the noisy element-wise measurements of $\mathbf{s}\mathbf{s}^T$, a generic problem that arises in statistics and machine learning. We study a mismatched Bayesian inference setting, where some of the parameters are not known to the statistician. We derive the full exact analytic expression of the asymptotic mean squared error (MSE) in the large system size limit for the particular case of Gaussian priors and additive noise. From our formulas, we see that estimation is still possible in the mismatched case; and also that the minimum MSE (MMSE) can be achieved if the statistician chooses suitable parameters. Our technique relies on the asymptotics of the spherical integrals and can be applied as long as the statistician chooses a rotationally invariant prior.

Rank-one matrix estimation: analytic time evolution of gradient descent dynamics

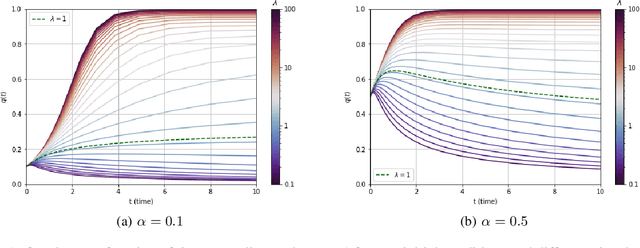
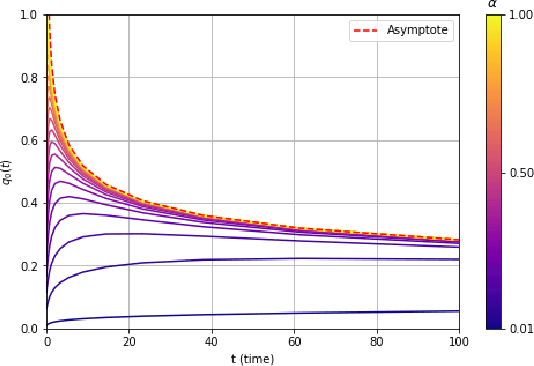
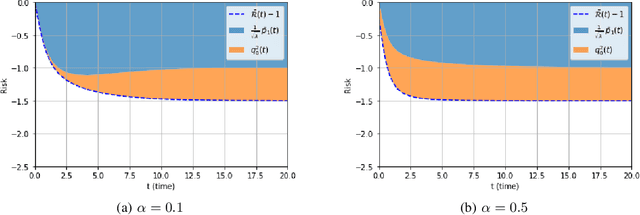
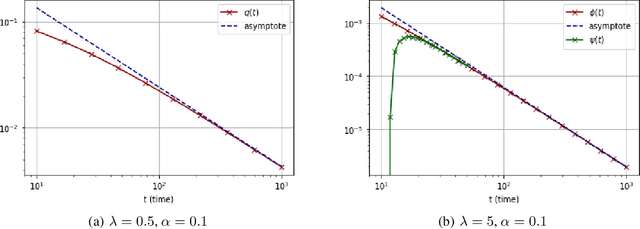
We consider a rank-one symmetric matrix corrupted by additive noise. The rank-one matrix is formed by an $n$-component unknown vector on the sphere of radius $\sqrt{n}$, and we consider the problem of estimating this vector from the corrupted matrix in the high dimensional limit of $n$ large, by gradient descent for a quadratic cost function on the sphere. Explicit formulas for the whole time evolution of the overlap between the estimator and unknown vector, as well as the cost, are rigorously derived. In the long time limit we recover the well known spectral phase transition, as a function of the signal-to-noise ratio. The explicit formulas also allow to point out interesting transient features of the time evolution. Our analysis technique is based on recent progress in random matrix theory and uses local versions of the semi-circle law.

Solving non-linear Kolmogorov equations in large dimensions by using deep learning: a numerical comparison of discretization schemes

Non-linear partial differential Kolmogorov equations are successfully used to describe a wide range of time dependent phenomena, in natural sciences, engineering or even finance. For example, in physical systems, the Allen-Cahn equation describes pattern formation associated to phase transitions. In finance, instead, the Black-Scholes equation describes the evolution of the price of derivative investment instruments. Such modern applications often require to solve these equations in high-dimensional regimes in which classical approaches are ineffective. Recently, an interesting new approach based on deep learning has been introduced by E, Han, and Jentzen [1][2]. The main idea is to construct a deep network which is trained from the samples of discrete stochastic differential equations underlying Kolmogorov's equation. The network is able to approximate, numerically at least, the solutions of the Kolmogorov equation with polynomial complexity in whole spatial domains. In this contribution we study variants of the deep networks by using different discretizations schemes of the stochastic differential equation. We compare the performance of the associated networks, on benchmarked examples, and show that, for some discretization schemes, improvements in the accuracy are possible without affecting the observed computational complexity.

Information theoretic limits of learning a sparse rule

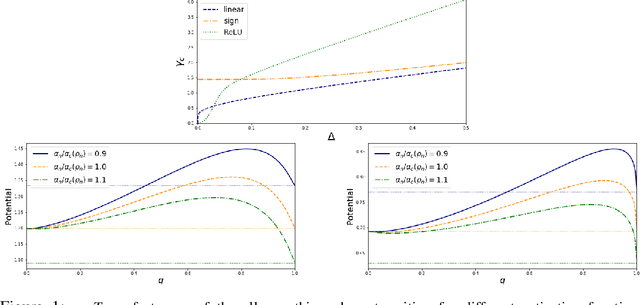
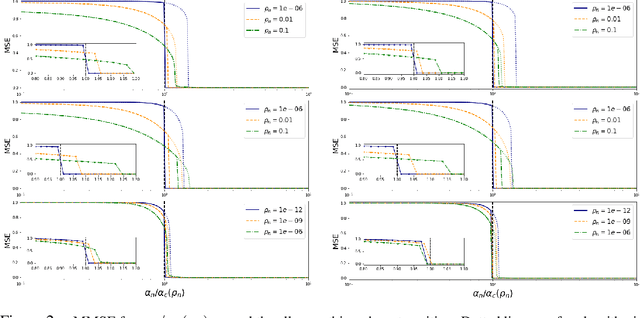
We consider generalized linear models in regimes where the number of nonzerocomponents of the signal and accessible data points are sublinear with respect to the size of the signal. We prove a variational formula for the asymptotic mutual information per sample when the system size grows to infinity. This result allows us to heuristically derive an expression for the minimum mean-square error (MMSE)of the Bayesian estimator. We then find that, for discrete signals and suitable vanishing scalings of the sparsity and sampling rate, the MMSE displays an all-or-nothing phenomenon, namely, the MMSE sharply jumps from its maximum value to zero at a critical sampling rate. The all-or-nothing phenomenon has recently been proved to occur in high-dimensional linear regression. Our analysis goes beyond the linear case and applies to learning the weights of a perceptron with general activation function in a teacher-student scenario. In particular we discuss an all-or-nothing phenomenon for the generalization error with a sublinear set of training examples.

All-or-nothing statistical and computational phase transitions in sparse spiked matrix estimation

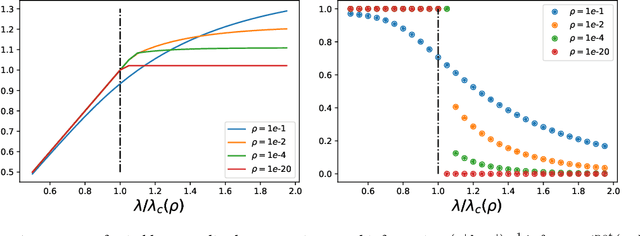
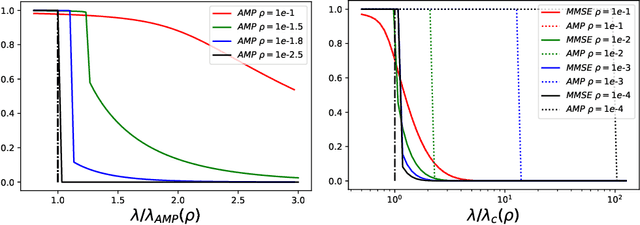
We determine statistical and computational limits for estimation of a rank-one matrix (the spike) corrupted by an additive gaussian noise matrix, in a sparse limit, where the underlying hidden vector (that constructs the rank-one matrix) has a number of non-zero components that scales sub-linearly with the total dimension of the vector, and the signal-to-noise ratio tends to infinity at an appropriate speed. We prove explicit low-dimensional variational formulas for the asymptotic mutual information between the spike and the observed noisy matrix and analyze the approximate message passing algorithm in the sparse regime. For Bernoulli and Bernoulli-Rademacher distributed vectors, and when the sparsity and signal strength satisfy an appropriate scaling relation, we find all-or-nothing phase transitions for the asymptotic minimum and algorithmic mean-square errors. These jump from their maximum possible value to zero, at well defined signal-to-noise thresholds whose asymptotic values we determine exactly. In the asymptotic regime the statistical-to-algorithmic gap diverges indicating that sparse recovery is hard for approximate message passing.