Multi-Group Proportional Representation

Image search and retrieval tasks can perpetuate harmful stereotypes, erase cultural identities, and amplify social disparities. Current approaches to mitigate these representational harms balance the number of retrieved items across population groups defined by a small number of (often binary) attributes. However, most existing methods overlook intersectional groups determined by combinations of group attributes, such as gender, race, and ethnicity. We introduce Multi-Group Proportional Representation (MPR), a novel metric that measures representation across intersectional groups. We develop practical methods for estimating MPR, provide theoretical guarantees, and propose optimization algorithms to ensure MPR in retrieval. We demonstrate that existing methods optimizing for equal and proportional representation metrics may fail to promote MPR. Crucially, our work shows that optimizing MPR yields more proportional representation across multiple intersectional groups specified by a rich function class, often with minimal compromise in retrieval accuracy.

A Comprehensive Study on Ziv-Zakai Lower Bounds on the MMSE

This paper explores Bayesian lower bounds on the minimum mean squared error (MMSE) that belong to the Ziv-Zakai (ZZ) family. The ZZ technique relies on connecting the bound to an M-ary hypothesis testing problem. Three versions of the ZZ bound (ZZB) exist: the first relies on the so-called valley-filling function (VFF), the second omits the VFF, and the third, i.e., the single-point ZZB (SZZB), uses a single point maximization. The first part of this paper provides the most general version of the bounds. First, it is shown that these bounds hold without any assumption on the distribution of the estimand. Second, the SZZB bound is extended to an M-ary setting and a version of it for the multivariate case is provided. In the second part, general properties of the bounds are provided. First, it is shown that all the bounds tensorize. Second, a complete characterization of the high-noise asymptotic is provided, which is used to argue about the tightness of the bounds. Third, the low-noise asymptotic is provided for mixed-input distributions and Gaussian additive noise channels. Specifically, in the low-noise, it is shown that the SZZB is not always tight. In the third part, the tightness of the bounds is evaluated. First, it is shown that in the low-noise regime the ZZB bound without the VFF is tight for mixed-input distributions and Gaussian additive noise channels. Second, for discrete inputs, the ZZB with the VFF is shown to be always sub-optimal, and equal to zero without the VFF. Third, unlike for the ZZB, an example is shown for which the SZZB is tight to the MMSE for discrete inputs. Fourth, sufficient and necessary conditions for the tightness of the bounds are provided. Finally, some examples are shown in which the bounds in the ZZ family outperform other well-known Bayesian bounds, i.e., the Cram\'er-Rao bound and the maximum entropy bound.

Data-Driven Estimation of the False Positive Rate of the Bayes Binary Classifier via Soft Labels

Classification is a fundamental task in many applications on which data-driven methods have shown outstanding performances. However, it is challenging to determine whether such methods have achieved the optimal performance. This is mainly because the best achievable performance is typically unknown and hence, effectively estimating it is of prime importance. In this paper, we consider binary classification problems and we propose an estimator for the false positive rate (FPR) of the Bayes classifier, that is, the optimal classifier with respect to accuracy, from a given dataset. Our method utilizes soft labels, or real-valued labels, which are gaining significant traction thanks to their properties. We thoroughly examine various theoretical properties of our estimator, including its consistency, unbiasedness, rate of convergence, and variance. To enhance the versatility of our estimator beyond soft labels, we also consider noisy labels, which encompass binary labels. For noisy labels, we develop effective FPR estimators by leveraging a denoising technique and the Nadaraya-Watson estimator. Due to the symmetry of the problem, our results can be readily applied to estimate the false negative rate of the Bayes classifier.

Functional Properties of the Ziv-Zakai bound with Arbitrary Inputs

This paper explores the Ziv-Zakai bound (ZZB), which is a well-known Bayesian lower bound on the Minimum Mean Squared Error (MMSE). First, it is shown that the ZZB holds without any assumption on the distribution of the estimand, that is, the estimand does not necessarily need to have a probability density function. The ZZB is then further analyzed in the high-noise and low-noise regimes and shown to always tensorize. Finally, the tightness of the ZZB is investigated under several aspects, such as the number of hypotheses and the usefulness of the valley-filling function. In particular, a sufficient and necessary condition for the tightness of the bound with continuous inputs is provided, and it is shown that the bound is never tight for discrete input distributions with a support set that does not have an accumulation point at zero.

Proactive Resilient Transmission and Scheduling Mechanisms for mmWave Networks

This paper aims to develop resilient transmission mechanisms to suitably distribute traffic across multiple paths in an arbitrary millimeter-wave (mmWave) network. The main contributions include: (a) the development of proactive transmission mechanisms that build resilience against network disruptions in advance, while achieving a high end-to-end packet rate; (b) the design of a heuristic path selection algorithm that efficiently selects (in polynomial time in the network size) multiple proactively resilient paths with high packet rates; and (c) the development of a hybrid scheduling algorithm that combines the proposed path selection algorithm with a deep reinforcement learning (DRL) based online approach for decentralized adaptation to blocked links and failed paths. To achieve resilience to link failures, a state-of-the-art Soft Actor-Critic DRL algorithm, which adapts the information flow through the network, is investigated. The proposed scheduling algorithm robustly adapts to link failures over different topologies, channel and blockage realizations while offering a superior performance to alternative algorithms.

An MMSE Lower Bound via Poincaré Inequality

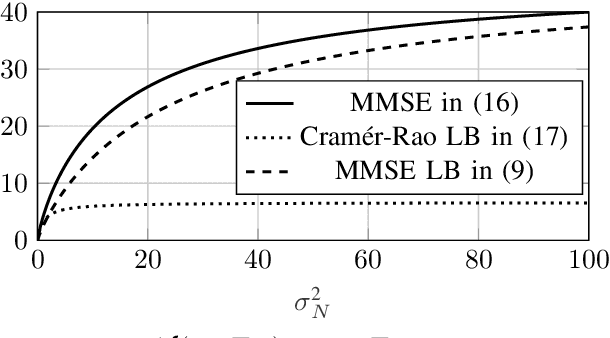
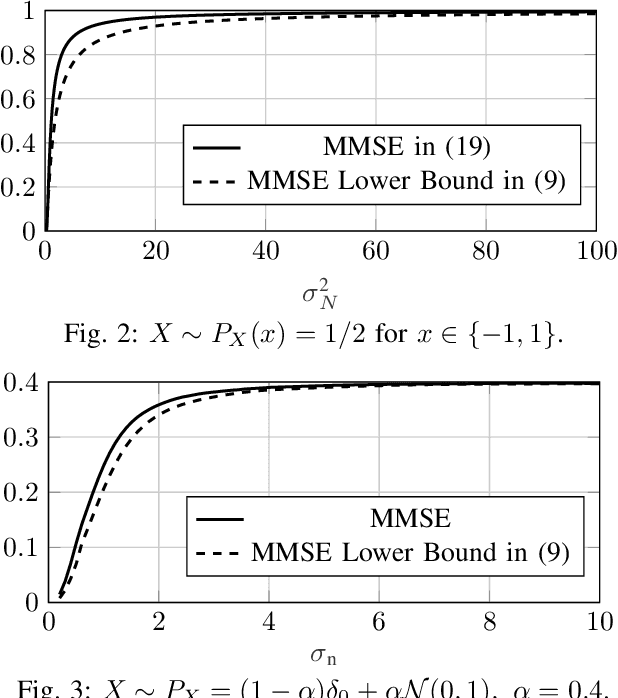
This paper studies the minimum mean squared error (MMSE) of estimating $\mathbf{X} \in \mathbb{R}^d$ from the noisy observation $\mathbf{Y} \in \mathbb{R}^k$, under the assumption that the noise (i.e., $\mathbf{Y}|\mathbf{X}$) is a member of the exponential family. The paper provides a new lower bound on the MMSE. Towards this end, an alternative representation of the MMSE is first presented, which is argued to be useful in deriving closed-form expressions for the MMSE. This new representation is then used together with the Poincar\'e inequality to provide a new lower bound on the MMSE. Unlike, for example, the Cram\'{e}r-Rao bound, the new bound holds for all possible distributions on the input $\mathbf{X}$. Moreover, the lower bound is shown to be tight in the high-noise regime for the Gaussian noise setting under the assumption that $\mathbf{X}$ is sub-Gaussian. Finally, several numerical examples are shown which demonstrate that the bound performs well in all noise regimes.

Entropic CLT for Order Statistics

It is well known that central order statistics exhibit a central limit behavior and converge to a Gaussian distribution as the sample size grows. This paper strengthens this known result by establishing an entropic version of the CLT that ensures a stronger mode of convergence using the relative entropy. In particular, an order $O(1/\sqrt{n})$ rate of convergence is established under mild conditions on the parent distribution of the sample generating the order statistics. To prove this result, ancillary results on order statistics are derived, which might be of independent interest.

Retrieving Data Permutations from Noisy Observations: High and Low Noise Asymptotics

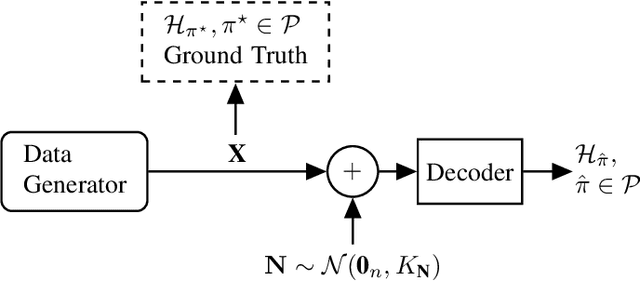
This paper considers the problem of recovering the permutation of an n-dimensional random vector X observed in Gaussian noise. First, a general expression for the probability of error is derived when a linear decoder (i.e., linear estimator followed by a sorting operation) is used. The derived expression holds with minimal assumptions on the distribution of X and when the noise has memory. Second, for the case of isotropic noise (i.e., noise with a diagonal scalar covariance matrix), the rates of convergence of the probability of error are characterized in the high and low noise regimes. In the low noise regime, for every dimension n, the probability of error is shown to behave proportionally to {\sigma}, where {\sigma} is the noise standard deviation. Moreover, the slope is computed exactly for several distributions and it is shown to behave quadratically in n. In the high noise regime, for every dimension n, the probability of correctness is shown to behave as 1/{\sigma}, and the exact expression for the rate of convergence is also provided.