Learning the score under shape constraints

Score estimation has recently emerged as a key modern statistical challenge, due to its pivotal role in generative modelling via diffusion models. Moreover, it is an essential ingredient in a new approach to linear regression via convex $M$-estimation, where the corresponding error densities are projected onto the log-concave class. Motivated by these applications, we study the minimax risk of score estimation with respect to squared $L^2(P_0)$-loss, where $P_0$ denotes an underlying log-concave distribution on $\mathbb{R}$. Such distributions have decreasing score functions, but on its own, this shape constraint is insufficient to guarantee a finite minimax risk. We therefore define subclasses of log-concave densities that capture two fundamental aspects of the estimation problem. First, we establish the crucial impact of tail behaviour on score estimation by determining the minimax rate over a class of log-concave densities whose score function exhibits controlled growth relative to the quantile levels. Second, we explore the interplay between smoothness and log-concavity by considering the class of log-concave densities with a scale restriction and a $(β,L)$-Hölder assumption on the log-density for some $β\in [1,2]$. We show that the minimax risk over this latter class is of order $L^{2/(2β+1)}n^{-β/(2β+1)}$ up to poly-logarithmic factors, where $n$ denotes the sample size. When $β< 2$, this rate is faster than could be obtained under either the shape constraint or the smoothness assumption alone. Our upper bounds are attained by a locally adaptive, multiscale estimator constructed from a uniform confidence band for the score function. This study highlights intriguing differences between the score estimation and density estimation problems over this shape-constrained class.

Deep learning with missing data

In the context of multivariate nonparametric regression with missing covariates, we propose Pattern Embedded Neural Networks (PENNs), which can be applied in conjunction with any existing imputation technique. In addition to a neural network trained on the imputed data, PENNs pass the vectors of observation indicators through a second neural network to provide a compact representation. The outputs are then combined in a third neural network to produce final predictions. Our main theoretical result exploits an assumption that the observation patterns can be partitioned into cells on which the Bayes regression function behaves similarly, and belongs to a compositional H\"older class. It provides a finite-sample excess risk bound that holds for an arbitrary missingness mechanism, and in combination with a complementary minimax lower bound, demonstrates that our PENN estimator attains in typical cases the minimax rate of convergence as if the cells of the partition were known in advance, up to a poly-logarithmic factor in the sample size. Numerical experiments on simulated, semi-synthetic and real data confirm that the PENN estimator consistently improves, often dramatically, on standard neural networks without pattern embedding. Code to reproduce our experiments, as well as a tutorial on how to apply our method, is publicly available.

High-probability minimax lower bounds

The minimax risk is often considered as a gold standard against which we can compare specific statistical procedures. Nevertheless, as has been observed recently in robust and heavy-tailed estimation problems, the inherent reduction of the (random) loss to its expectation may entail a significant loss of information regarding its tail behaviour. In an attempt to avoid such a loss, we introduce the notion of a minimax quantile, and seek to articulate its dependence on the quantile level. To this end, we develop high-probability variants of the classical Le Cam and Fano methods, as well as a technique to convert local minimax risk lower bounds to lower bounds on minimax quantiles. To illustrate the power of our framework, we deploy our techniques on several examples, recovering recent results in robust mean estimation and stochastic convex optimisation, as well as obtaining several new results in covariance matrix estimation, sparse linear regression, nonparametric density estimation and isotonic regression. Our overall goal is to argue that minimax quantiles can provide a finer-grained understanding of the difficulty of statistical problems, and that, in wide generality, lower bounds on these quantities can be obtained via user-friendly tools.

Optimal convex $M$-estimation via score matching

In the context of linear regression, we construct a data-driven convex loss function with respect to which empirical risk minimisation yields optimal asymptotic variance in the downstream estimation of the regression coefficients. Our semiparametric approach targets the best decreasing approximation of the derivative of the log-density of the noise distribution. At the population level, this fitting process is a nonparametric extension of score matching, corresponding to a log-concave projection of the noise distribution with respect to the Fisher divergence. The procedure is computationally efficient, and we prove that our procedure attains the minimal asymptotic covariance among all convex $M$-estimators. As an example of a non-log-concave setting, for Cauchy errors, the optimal convex loss function is Huber-like, and our procedure yields an asymptotic efficiency greater than 0.87 relative to the oracle maximum likelihood estimator of the regression coefficients that uses knowledge of this error distribution; in this sense, we obtain robustness without sacrificing much efficiency. Numerical experiments confirm the practical merits of our proposal.

Sharp-SSL: Selective high-dimensional axis-aligned random projections for semi-supervised learning

We propose a new method for high-dimensional semi-supervised learning problems based on the careful aggregation of the results of a low-dimensional procedure applied to many axis-aligned random projections of the data. Our primary goal is to identify important variables for distinguishing between the classes; existing low-dimensional methods can then be applied for final class assignment. Motivated by a generalized Rayleigh quotient, we score projections according to the traces of the estimated whitened between-class covariance matrices on the projected data. This enables us to assign an importance weight to each variable for a given projection, and to select our signal variables by aggregating these weights over high-scoring projections. Our theory shows that the resulting Sharp-SSL algorithm is able to recover the signal coordinates with high probability when we aggregate over sufficiently many random projections and when the base procedure estimates the whitened between-class covariance matrix sufficiently well. The Gaussian EM algorithm is a natural choice as a base procedure, and we provide a new analysis of its performance in semi-supervised settings that controls the parameter estimation error in terms of the proportion of labeled data in the sample. Numerical results on both simulated data and a real colon tumor dataset support the excellent empirical performance of the method.

The Projected Covariance Measure for assumption-lean variable significance testing

Testing the significance of a variable or group of variables $X$ for predicting a response $Y$, given additional covariates $Z$, is a ubiquitous task in statistics. A simple but common approach is to specify a linear model, and then test whether the regression coefficient for $X$ is non-zero. However, when the model is misspecified, the test may have poor power, for example when $X$ is involved in complex interactions, or lead to many false rejections. In this work we study the problem of testing the model-free null of conditional mean independence, i.e. that the conditional mean of $Y$ given $X$ and $Z$ does not depend on $X$. We propose a simple and general framework that can leverage flexible nonparametric or machine learning methods, such as additive models or random forests, to yield both robust error control and high power. The procedure involves using these methods to perform regressions, first to estimate a form of projection of $Y$ on $X$ and $Z$ using one half of the data, and then to estimate the expected conditional covariance between this projection and $Y$ on the remaining half of the data. While the approach is general, we show that a version of our procedure using spline regression achieves what we show is the minimax optimal rate in this nonparametric testing problem. Numerical experiments demonstrate the effectiveness of our approach both in terms of maintaining Type I error control, and power, compared to several existing approaches.

Optimal subgroup selection

In clinical trials and other applications, we often see regions of the feature space that appear to exhibit interesting behaviour, but it is unclear whether these observed phenomena are reflected at the population level. Focusing on a regression setting, we consider the subgroup selection challenge of identifying a region of the feature space on which the regression function exceeds a pre-determined threshold. We formulate the problem as one of constrained optimisation, where we seek a low-complexity, data-dependent selection set on which, with a guaranteed probability, the regression function is uniformly at least as large as the threshold; subject to this constraint, we would like the region to contain as much mass under the marginal feature distribution as possible. This leads to a natural notion of regret, and our main contribution is to determine the minimax optimal rate for this regret in both the sample size and the Type I error probability. The rate involves a delicate interplay between parameters that control the smoothness of the regression function, as well as exponents that quantify the extent to which the optimal selection set at the population level can be approximated by families of well-behaved subsets. Finally, we expand the scope of our previous results by illustrating how they may be generalised to a treatment and control setting, where interest lies in the heterogeneous treatment effect.

Adaptive transfer learning

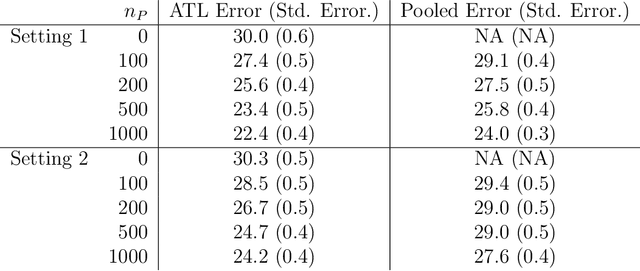
In transfer learning, we wish to make inference about a target population when we have access to data both from the distribution itself, and from a different but related source distribution. We introduce a flexible framework for transfer learning in the context of binary classification, allowing for covariate-dependent relationships between the source and target distributions that are not required to preserve the Bayes decision boundary. Our main contributions are to derive the minimax optimal rates of convergence (up to poly-logarithmic factors) in this problem, and show that the optimal rate can be achieved by an algorithm that adapts to key aspects of the unknown transfer relationship, as well as the smoothness and tail parameters of our distributional classes. This optimal rate turns out to have several regimes, depending on the interplay between the relative sample sizes and the strength of the transfer relationship, and our algorithm achieves optimality by careful, decision tree-based calibration of local nearest-neighbour procedures.

A unifying tutorial on Approximate Message Passing

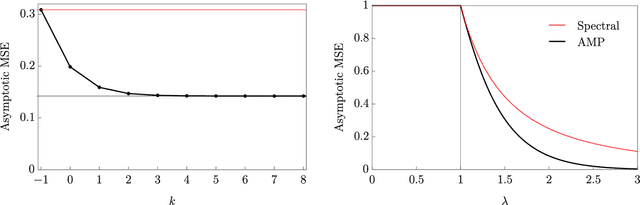
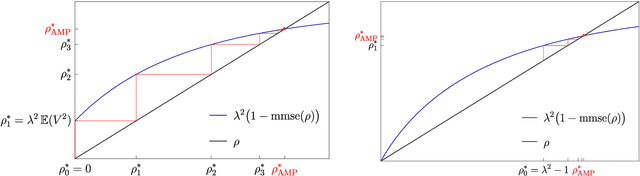
Over the last decade or so, Approximate Message Passing (AMP) algorithms have become extremely popular in various structured high-dimensional statistical problems. The fact that the origins of these techniques can be traced back to notions of belief propagation in the statistical physics literature lends a certain mystique to the area for many statisticians. Our goal in this work is to present the main ideas of AMP from a statistical perspective, to illustrate the power and flexibility of the AMP framework. Along the way, we strengthen and unify many of the results in the existing literature.

USP: an independence test that improves on Pearson's chi-squared and the $G$-test

We present the $U$-Statistic Permutation (USP) test of independence in the context of discrete data displayed in a contingency table. Either Pearson's chi-squared test of independence, or the $G$-test, are typically used for this task, but we argue that these tests have serious deficiencies, both in terms of their inability to control the size of the test, and their power properties. By contrast, the USP test is guaranteed to control the size of the test at the nominal level for all sample sizes, has no issues with small (or zero) cell counts, and is able to detect distributions that violate independence in only a minimal way. The test statistic is derived from a $U$-statistic estimator of a natural population measure of dependence, and we prove that this is the unique minimum variance unbiased estimator of this population quantity. The practical utility of the USP test is demonstrated on both simulated data, where its power can be dramatically greater than those of Pearson's test and the $G$-test, and on real data. The USP test is implemented in the R package USP.