An AI-driven framework for the prediction of personalised health response to air pollution

Air pollution poses a significant threat to public health, causing or exacerbating many respiratory and cardiovascular diseases. In addition, climate change is bringing about more extreme weather events such as wildfires and heatwaves, which can increase levels of pollution and worsen the effects of pollution exposure. Recent advances in personal sensing have transformed the collection of behavioural and physiological data, leading to the potential for new improvements in healthcare. We wish to capitalise on this data, alongside new capabilities in AI for making time series predictions, in order to monitor and predict health outcomes for an individual. Thus, we present a novel workflow for predicting personalised health responses to pollution by integrating physiological data from wearable fitness devices with real-time environmental exposures. The data is collected from various sources in a secure and ethical manner, and is used to train an AI model to predict individual health responses to pollution exposure within a cloud-based, modular framework. We demonstrate that the AI model -- an Adversarial Autoencoder neural network in this case -- accurately reconstructs time-dependent health signals and captures nonlinear responses to pollution. Transfer learning is applied using data from a personal smartwatch, which increases the generalisation abilities of the AI model and illustrates the adaptability of the approach to real-world, user-generated data.

Parameter estimation for land-surface models using machine learning libraries

The Neural Networks for Partial Differential Equations (NN4PDEs) approach is used to determine the parameters of a simple land-surface model using PyTorch's backpropagation engine. In order to test the inverse model, a synthetic dataset is created by running the model in forward mode with known parameter values to create soil temperature time series that can be used as observations for the inverse model. We show that it is not possible to obtain a reliable parameter estimation using a single observed soil temperature time series. Using measurements at two depths, reliable parameter estimates can be obtained although it is not possible to differentiate between latent and sensible heat fluxes. We apply the inverse model to urban flux tower data in Phoenix, United States, and show that the thermal conductivity, volumetric heat capacity, and the combined sensible-latent heat transfer coefficient can be reliably estimated using an observed value for the effective surface albedo. The resulting model accurately predicts the outgoing longwave radiation, conductive soil fluxes and the combined sensible-latent heat fluxes.

Using AI libraries for Incompressible Computational Fluid Dynamics

Recently, there has been a huge effort focused on developing highly efficient open source libraries to perform Artificial Intelligence (AI) related computations on different computer architectures (for example, CPUs, GPUs and new AI processors). This has not only made the algorithms based on these libraries highly efficient and portable between different architectures, but also has substantially simplified the entry barrier to develop methods using AI. Here, we present a novel methodology to bring the power of both AI software and hardware into the field of numerical modelling by repurposing AI methods, such as Convolutional Neural Networks (CNNs), for the standard operations required in the field of the numerical solution of Partial Differential Equations (PDEs). The aim of this work is to bring the high performance, architecture agnosticism and ease of use into the field of the numerical solution of PDEs. We use the proposed methodology to solve the advection-diffusion equation, the non-linear Burgers equation and incompressible flow past a bluff body. For the latter, a convolutional neural network is used as a multigrid solver in order to enforce the incompressibility constraint. We show that the presented methodology can solve all these problems using repurposed AI libraries in an efficient way, and presents a new avenue to explore in the development of methods to solve PDEs and Computational Fluid Dynamics problems with implicit methods.

Solving the Discretised Multiphase Flow Equations with Interface Capturing on Structured Grids Using Machine Learning Libraries

This paper solves the multiphase flow equations with interface capturing using the AI4PDEs approach (Artificial Intelligence for Partial Differential Equations). The solver within AI4PDEs uses tools from machine learning (ML) libraries to solve (exactly) partial differential equations (PDEs) that have been discretised using numerical methods. Convolutional layers can be used to express the discretisations as a neural network, whose weights are determined by the numerical method, rather than by training. To solve the system, a multigrid solver is implemented through a neural network with a U-Net architecture. Immiscible two-phase flow is modelled by the 3D incompressible Navier-Stokes equations with surface tension and advection of a volume fraction field, which describes the interface between the fluids. A new compressive algebraic volume-of-fluids method is introduced, based on a residual formulation using Petrov-Galerkin for accuracy and designed with AI4PDEs in mind. High-order finite-element based schemes are chosen to model a collapsing water column and a rising bubble. Results compare well with experimental data and other numerical results from the literature, demonstrating that, for the first time, finite element discretisations of multiphase flows can be solved using the neural network solver from the AI4PDEs approach. A benefit of expressing numerical discretisations as neural networks is that the code can run, without modification, on CPUs, GPUs or the latest accelerators designed especially to run AI codes.

An AI-based Domain-Decomposition Non-Intrusive Reduced-Order Model for Extended Domains applied to Multiphase Flow in Pipes

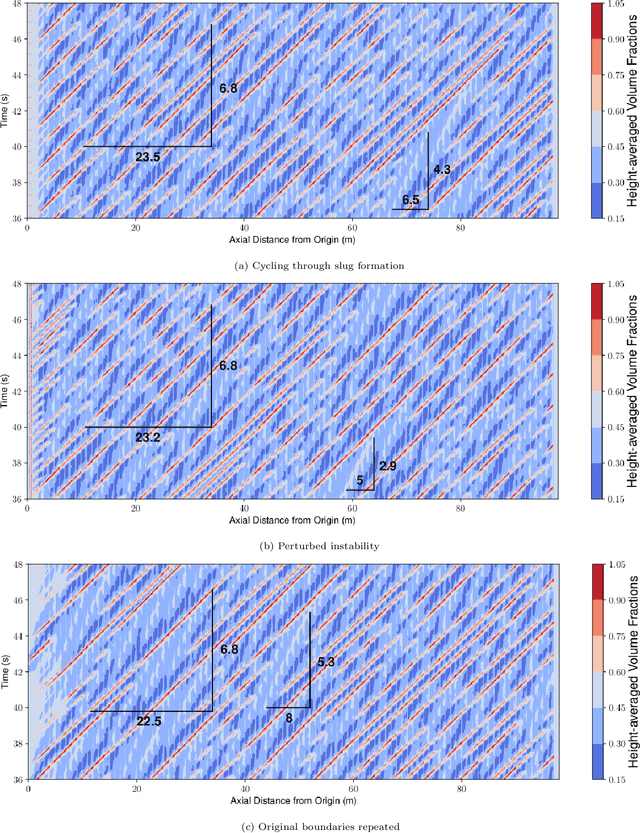
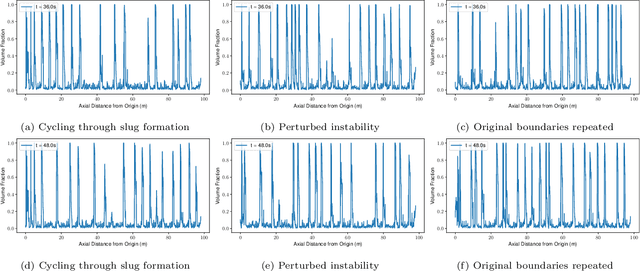
The modelling of multiphase flow in a pipe presents a significant challenge for high-resolution computational fluid dynamics (CFD) models due to the high aspect ratio (length over diameter) of the domain. In subsea applications, the pipe length can be several hundreds of kilometres versus a pipe diameter of just a few inches. In this paper, we present a new AI-based non-intrusive reduced-order model within a domain decomposition framework (AI-DDNIROM) which is capable of making predictions for domains significantly larger than the domain used in training. This is achieved by using domain decomposition; dimensionality reduction; training a neural network to make predictions for a single subdomain; and by using an iteration-by-subdomain technique to converge the solution over the whole domain. To find the low-dimensional space, we explore several types of autoencoder networks, known for their ability to compress information accurately and compactly. The performance of the autoencoders is assessed on two advection-dominated problems: flow past a cylinder and slug flow in a pipe. To make predictions in time, we exploit an adversarial network which aims to learn the distribution of the training data, in addition to learning the mapping between particular inputs and outputs. This type of network has shown the potential to produce realistic outputs. The whole framework is applied to multiphase slug flow in a horizontal pipe for which an AI-DDNIROM is trained on high-fidelity CFD simulations of a pipe of length 10 m with an aspect ratio of 13:1, and tested by simulating the flow for a pipe of length 98 m with an aspect ratio of almost 130:1. Statistics of the flows obtained from the CFD simulations are compared to those of the AI-DDNIROM predictions to demonstrate the success of our approach.

GAN for time series prediction, data assimilation and uncertainty quantification

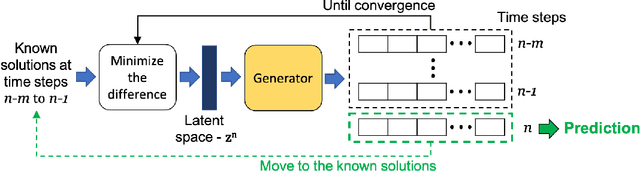
We propose a new method in which a generative adversarial network (GAN) is used to quantify the uncertainty of forward simulations in the presence of observed data. Previously, a method has been developed which enables GANs to make time series predictions and data assimilation by training a GAN with unconditional simulations of a high-fidelity numerical model. After training, the GAN can be used to predict the evolution of the spatial distribution of the simulation states and observed data is assimilated. In this paper, we describe the process required in order to quantify uncertainty, during which no additional simulations of the high-fidelity numerical model are required. These methods take advantage of the adjoint-like capabilities of generative models and the ability to simulate forwards and backwards in time. Set within a reduced-order model framework for efficiency, we apply these methods to a compartmental model in epidemiology to predict the spread of COVID-19 in an idealised town. The results show that the proposed method can efficiently quantify uncertainty in the presence of measurements using only unconditional simulations of the high-fidelity numerical model.

Digital twins based on bidirectional LSTM and GAN for modelling COVID-19

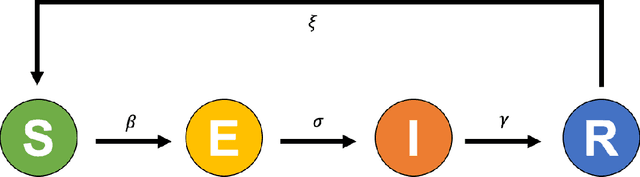
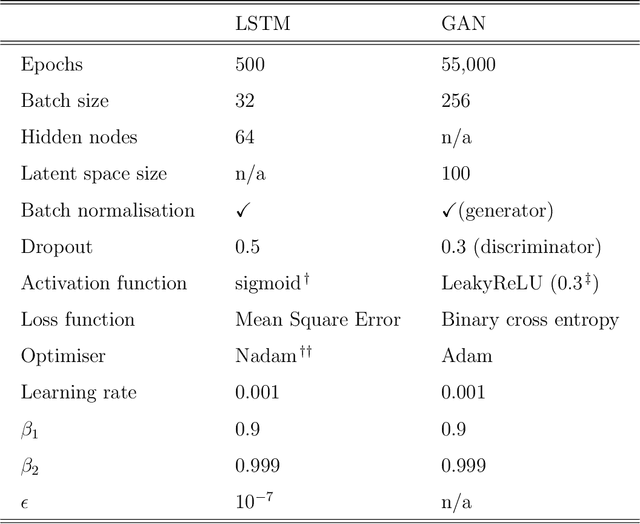
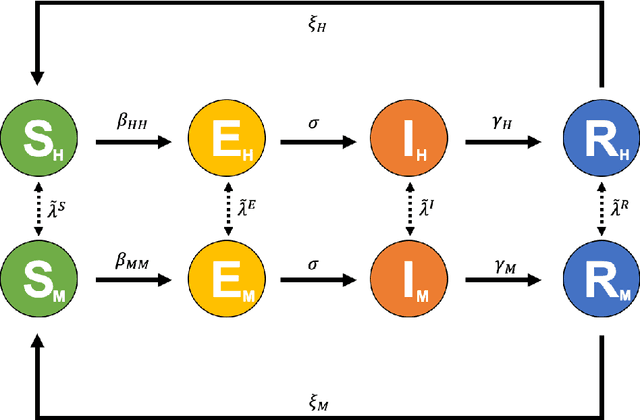
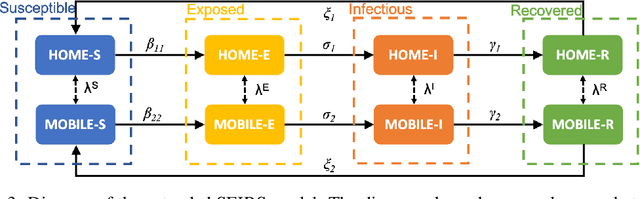
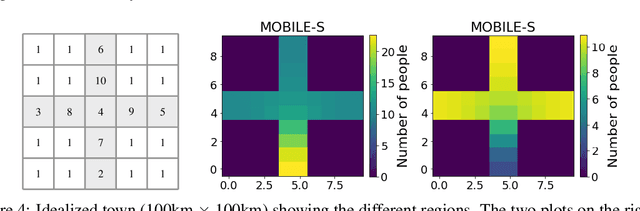
The outbreak of the coronavirus disease 2019 (COVID-19) has now spread throughout the globe infecting over 100 million people and causing the death of over 2.2 million people. Thus, there is an urgent need to study the dynamics of epidemiological models to gain a better understanding of how such diseases spread. While epidemiological models can be computationally expensive, recent advances in machine learning techniques have given rise to neural networks with the ability to learn and predict complex dynamics at reduced computational costs. Here we introduce two digital twins of a SEIRS model applied to an idealised town. The SEIRS model has been modified to take account of spatial variation and, where possible, the model parameters are based on official virus spreading data from the UK. We compare predictions from a data-corrected Bidirectional Long Short-Term Memory network and a predictive Generative Adversarial Network. The predictions given by these two frameworks are accurate when compared to the original SEIRS model data. Additionally, these frameworks are data-agnostic and could be applied to towns, idealised or real, in the UK or in other countries. Also, more compartments could be included in the SEIRS model, in order to study more realistic epidemiological behaviour.

An autoencoder-based reduced-order model for eigenvalue problems with application to neutron diffusion

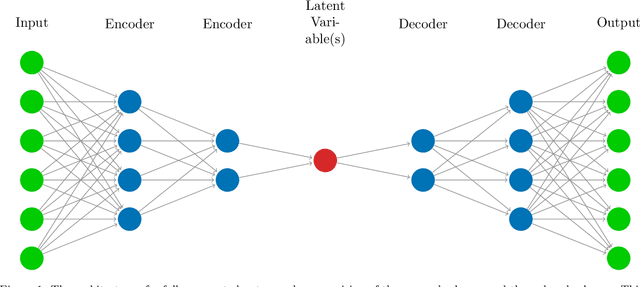
Using an autoencoder for dimensionality reduction, this paper presents a novel projection-based reduced-order model for eigenvalue problems. Reduced-order modelling relies on finding suitable basis functions which define a low-dimensional space in which a high-dimensional system is approximated. Proper orthogonal decomposition (POD) and singular value decomposition (SVD) are often used for this purpose and yield an optimal linear subspace. Autoencoders provide a nonlinear alternative to POD/SVD, that may capture, more efficiently, features or patterns in the high-fidelity model results. Reduced-order models based on an autoencoder and a novel hybrid SVD-autoencoder are developed. These methods are compared with the standard POD-Galerkin approach and are applied to two test cases taken from the field of nuclear reactor physics.