Mitigating loss of variance in ensemble data assimilation: machine learning-based and distance-free localizations for better covariance estimation

We propose two new methods based/inspired by machine learning for tabular data and distance-free localization to enhance the covariance estimations in an ensemble data assimilation. The main goal is to enhance the data assimilation results by mitigating loss of variance due to sampling errors. We also analyze the suitability of several machine learning models and the balance between accuracy and computational cost of the covariance estimations. We introduce two distance-free localization techniques leveraging machine learning methods specifically tailored for tabular data. The methods are integrated into the Ensemble Smoother with Multiple Data Assimilation (ES-MDA) framework. The results show that the proposed localizations improve covariance accuracy and enhance data assimilation and uncertainty quantification results. We observe reduced variance loss for the input variables using the proposed methods. Furthermore, we compare several machine learning models, assessing their suitability for the problem in terms of computational cost, and quality of the covariance estimation and data match. The influence of ensemble size is also investigated, providing insights into balancing accuracy and computational efficiency. Our findings demonstrate that certain machine learning models are more suitable for this problem. This study introduces two novel methods that mitigate variance loss for model parameters in ensemble-based data assimilation, offering practical solutions that are easy to implement and do not require any additional numerical simulation or hyperparameter tuning.

GAN for time series prediction, data assimilation and uncertainty quantification

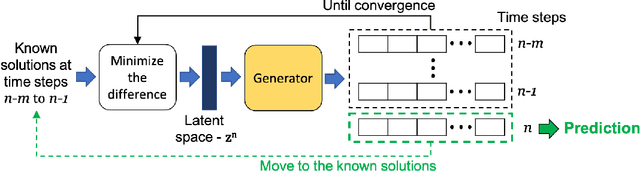
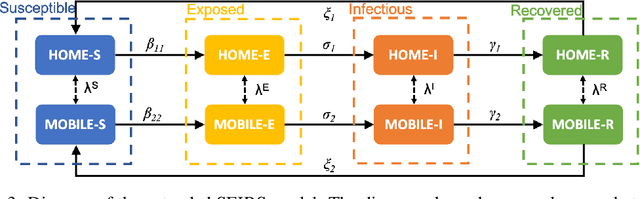
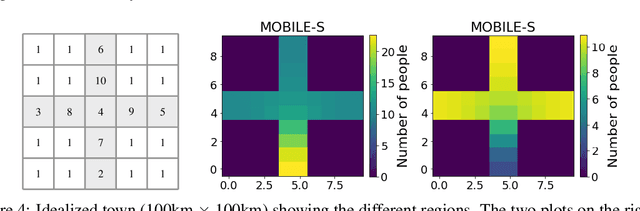
We propose a new method in which a generative adversarial network (GAN) is used to quantify the uncertainty of forward simulations in the presence of observed data. Previously, a method has been developed which enables GANs to make time series predictions and data assimilation by training a GAN with unconditional simulations of a high-fidelity numerical model. After training, the GAN can be used to predict the evolution of the spatial distribution of the simulation states and observed data is assimilated. In this paper, we describe the process required in order to quantify uncertainty, during which no additional simulations of the high-fidelity numerical model are required. These methods take advantage of the adjoint-like capabilities of generative models and the ability to simulate forwards and backwards in time. Set within a reduced-order model framework for efficiency, we apply these methods to a compartmental model in epidemiology to predict the spread of COVID-19 in an idealised town. The results show that the proposed method can efficiently quantify uncertainty in the presence of measurements using only unconditional simulations of the high-fidelity numerical model.