Model Analysis And Design Of Ellipse Based Segmented Varying Curved Foot For Biped Robot Walking

This paper presents the modeling, design, and experimental validation of an Ellipse-based Segmented Varying Curvature (ESVC) foot for bipedal robots. Inspired by the segmented curvature rollover shape of human feet, the ESVC foot aims to enhance gait energy efficiency while maintaining analytical tractability for foot location based controller. First, we derive a complete analytical contact model for the ESVC foot by formulating spatial transformations of elliptical segments only using elementary functions. Then a nonlinear programming approach is engaged to determine optimal elliptical parameters of hind foot and fore foot based on a known mid-foot. An error compensation method is introduced to address approximation inaccuracies in rollover length calculation. The proposed ESVC foot is then integrated with a Hybrid Linear Inverted Pendulum model-based walking controller and validated through both simulation and physical experiments on the TT II biped robot. Experimental results across marking time, sagittal, and lateral walking tasks show that the ESVC foot consistently reduces energy consumption compared to line, and flat feet, with up to 18.52\% improvement in lateral walking. These findings demonstrate that the ESVC foot provides a practical and energy-efficient alternative for real-world bipedal locomotion. The proposed design methodology also lays a foundation for data-driven foot shape optimization in future research.

An AI-driven framework for the prediction of personalised health response to air pollution

Air pollution poses a significant threat to public health, causing or exacerbating many respiratory and cardiovascular diseases. In addition, climate change is bringing about more extreme weather events such as wildfires and heatwaves, which can increase levels of pollution and worsen the effects of pollution exposure. Recent advances in personal sensing have transformed the collection of behavioural and physiological data, leading to the potential for new improvements in healthcare. We wish to capitalise on this data, alongside new capabilities in AI for making time series predictions, in order to monitor and predict health outcomes for an individual. Thus, we present a novel workflow for predicting personalised health responses to pollution by integrating physiological data from wearable fitness devices with real-time environmental exposures. The data is collected from various sources in a secure and ethical manner, and is used to train an AI model to predict individual health responses to pollution exposure within a cloud-based, modular framework. We demonstrate that the AI model -- an Adversarial Autoencoder neural network in this case -- accurately reconstructs time-dependent health signals and captures nonlinear responses to pollution. Transfer learning is applied using data from a personal smartwatch, which increases the generalisation abilities of the AI model and illustrates the adaptability of the approach to real-world, user-generated data.

Predicting Open-Hole Laminates Failure Using Support Vector Machines With Classical and Quantum Kernels

Modeling open hole failure of composites is a complex task, consisting in a highly nonlinear response with interacting failure modes. Numerical modeling of this phenomenon has traditionally been based on the finite element method, but requires to tradeoff between high fidelity and computational cost. To mitigate this shortcoming, recent work has leveraged machine learning to predict the strength of open hole composite specimens. Here, we also propose using data-based models but to tackle open hole composite failure from a classification point of view. More specifically, we show how to train surrogate models to learn the ultimate failure envelope of an open hole composite plate under in-plane loading. To achieve this, we solve the classification problem via support vector machine (SVM) and test different classifiers by changing the SVM kernel function. The flexibility of kernel-based SVM also allows us to integrate the recently developed quantum kernels in our algorithm and compare them with the standard radial basis function (RBF) kernel. Finally, thanks to kernel-target alignment optimization, we tune the free parameters of all kernels to best separate safe and failure-inducing loading states. The results show classification accuracies higher than 90% for RBF, especially after alignment, followed closely by the quantum kernel classifiers.

Using AI libraries for Incompressible Computational Fluid Dynamics

Recently, there has been a huge effort focused on developing highly efficient open source libraries to perform Artificial Intelligence (AI) related computations on different computer architectures (for example, CPUs, GPUs and new AI processors). This has not only made the algorithms based on these libraries highly efficient and portable between different architectures, but also has substantially simplified the entry barrier to develop methods using AI. Here, we present a novel methodology to bring the power of both AI software and hardware into the field of numerical modelling by repurposing AI methods, such as Convolutional Neural Networks (CNNs), for the standard operations required in the field of the numerical solution of Partial Differential Equations (PDEs). The aim of this work is to bring the high performance, architecture agnosticism and ease of use into the field of the numerical solution of PDEs. We use the proposed methodology to solve the advection-diffusion equation, the non-linear Burgers equation and incompressible flow past a bluff body. For the latter, a convolutional neural network is used as a multigrid solver in order to enforce the incompressibility constraint. We show that the presented methodology can solve all these problems using repurposed AI libraries in an efficient way, and presents a new avenue to explore in the development of methods to solve PDEs and Computational Fluid Dynamics problems with implicit methods.

Solving the Discretised Multiphase Flow Equations with Interface Capturing on Structured Grids Using Machine Learning Libraries

This paper solves the multiphase flow equations with interface capturing using the AI4PDEs approach (Artificial Intelligence for Partial Differential Equations). The solver within AI4PDEs uses tools from machine learning (ML) libraries to solve (exactly) partial differential equations (PDEs) that have been discretised using numerical methods. Convolutional layers can be used to express the discretisations as a neural network, whose weights are determined by the numerical method, rather than by training. To solve the system, a multigrid solver is implemented through a neural network with a U-Net architecture. Immiscible two-phase flow is modelled by the 3D incompressible Navier-Stokes equations with surface tension and advection of a volume fraction field, which describes the interface between the fluids. A new compressive algebraic volume-of-fluids method is introduced, based on a residual formulation using Petrov-Galerkin for accuracy and designed with AI4PDEs in mind. High-order finite-element based schemes are chosen to model a collapsing water column and a rising bubble. Results compare well with experimental data and other numerical results from the literature, demonstrating that, for the first time, finite element discretisations of multiphase flows can be solved using the neural network solver from the AI4PDEs approach. A benefit of expressing numerical discretisations as neural networks is that the code can run, without modification, on CPUs, GPUs or the latest accelerators designed especially to run AI codes.

Analyzing Convergence in Quantum Neural Networks: Deviations from Neural Tangent Kernels

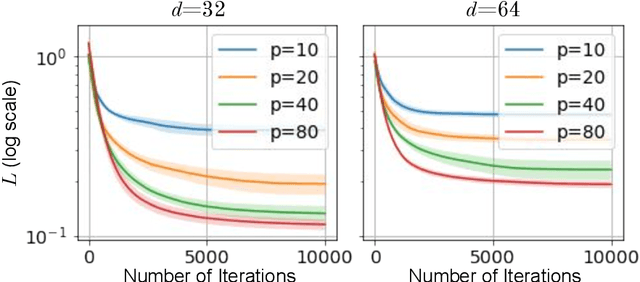
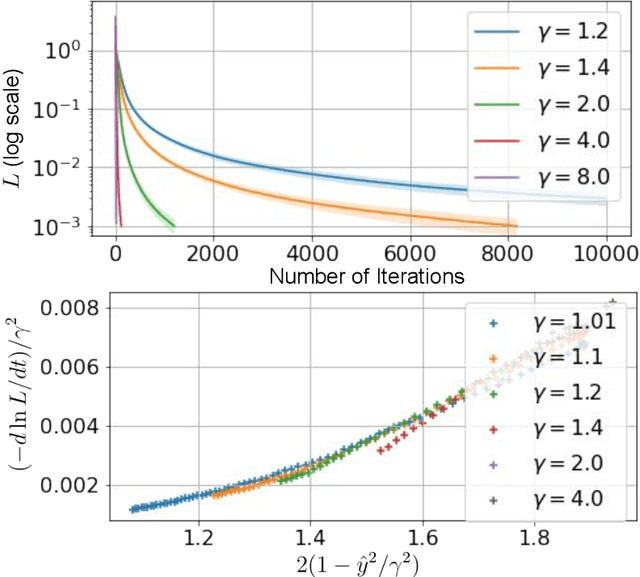
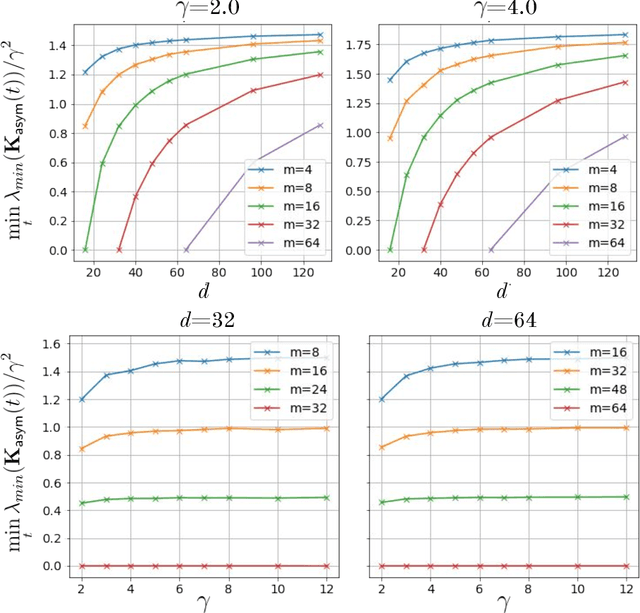
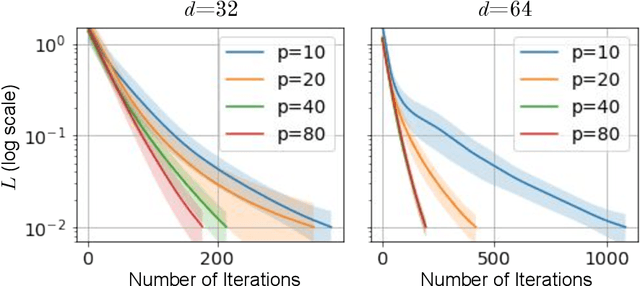
A quantum neural network (QNN) is a parameterized mapping efficiently implementable on near-term Noisy Intermediate-Scale Quantum (NISQ) computers. It can be used for supervised learning when combined with classical gradient-based optimizers. Despite the existing empirical and theoretical investigations, the convergence of QNN training is not fully understood. Inspired by the success of the neural tangent kernels (NTKs) in probing into the dynamics of classical neural networks, a recent line of works proposes to study over-parameterized QNNs by examining a quantum version of tangent kernels. In this work, we study the dynamics of QNNs and show that contrary to popular belief it is qualitatively different from that of any kernel regression: due to the unitarity of quantum operations, there is a non-negligible deviation from the tangent kernel regression derived at the random initialization. As a result of the deviation, we prove the at-most sublinear convergence for QNNs with Pauli measurements, which is beyond the explanatory power of any kernel regression dynamics. We then present the actual dynamics of QNNs in the limit of over-parameterization. The new dynamics capture the change of convergence rate during training and implies that the range of measurements is crucial to the fast QNN convergence.